System.Drawing.Drawing2D.Matrix class
This article provides supplementary remarks to the reference documentation for this API.
The Matrix class encapsulates a 3-by-3 affine matrix that represents a geometric transform.
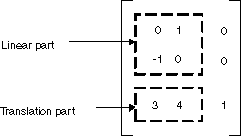
In GDI+, you can store an affine transformation in a Matrix object. Because the third column of a matrix that represents an affine transformation is always (0, 0, 1), you specify only the six numbers in the first two columns when you construct a Matrix object. The statement Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) constructs the matrix shown in the following figure.
Note
In .NET 6 and later versions, the System.Drawing.Common package, which includes this type, is only supported on Windows operating systems. Use of this type in cross-platform apps causes compile-time warnings and run-time exceptions. For more information, see System.Drawing.Common only supported on Windows.
Composite transformations
A composite transformation is a sequence of transformations, one followed by the other. Consider the matrices and transformations in the following list:
| Matrix | Transformation |
|---|---|
| Matrix A | Rotate 90 degrees |
| Matrix B | Scale by a factor of 2 in the x direction |
| Matrix C | Translate 3 units in the y direction |
If you start with the point (2, 1) - represented by the matrix [2 1 1] - and multiply by A, then B, then C, the point (2, 1) will undergo the three transformations in the order listed.
[2 1 1]ABC = [-2 5 1]
Rather than store the three parts of the composite transformation in three separate matrices, you can multiply A, B, and C together to get a single 3×3 matrix that stores the entire composite transformation. Suppose ABC = D. Then a point multiplied by D gives the same result as a point multiplied by A, then B, then C.
[2 1 1]D = [-2 5 1]
The following illustration shows the matrices A, B, C, and D.
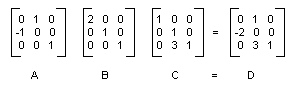
The fact that the matrix of a composite transformation can be formed by multiplying the individual transformation matrices means that any sequence of affine transformations can be stored in a single Matrix object.
Caution
The order of a composite transformation is important. In general, rotate, then scale, then translate is not the same as scale, then rotate, then translate. Similarly, the order of matrix multiplication is important. In general, ABC is not the same as BAC.
The Matrix class provides several methods for building a composite transformation: Multiply, Rotate, RotateAt, Scale, Shear, and Translate. The following example creates the matrix of a composite transformation that first rotates 30 degrees, then scales by a factor of 2 in the y direction, and then translates 5 units in the x direction:
Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);
Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)
