Small Basic: Coordinate
This article describes about coordinates in Microsoft Small Basic programming language.
Coordinate
A coordinate (or co-ordinate) is a number represents a position in a line. With two lines that are called x-axis and y-axis, any position can be described in a 2-D surface as a couple of coordinates such like (10, 20). In Small Basic, there are two types of coordinates. One is for Desktop. Another is for GraphicsWindow.
Desktop Coordinate
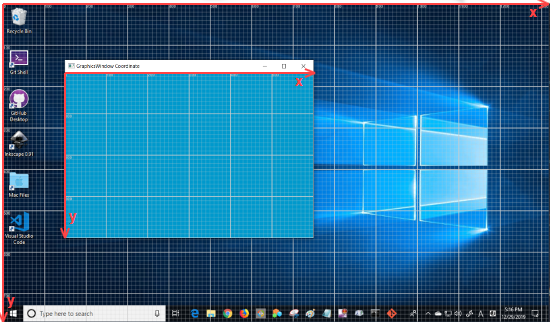
The origin of the Desktop coordinate is the left top corner of the desktop. Properties Mouse.MouseX, Mouse.MouseY, GraphicsWindow.Left, and GraphicsWindow.Top show positions in Desktop coordinates.
GraphicsWindow Coordinate
The origin of the GraphicsWindow coordinate is the left top corner of the graphics window application pain. GraphicsWindow coordinate is used in many properties and operations in GraphicsWindow and Shapes objects. Following figure shows Desktop coordinate and GraphicsWindow coordinate.
Coordinate Transformation
Many application programs have their own coordinates. So coordinate transformation is needed to convert application coordinate such as (x, y) to the graphics window coordinate such as (gx, gy). In Maths, y-axis goes from bottom to top, but in the graphics window, y-axis goes from top to bottom. Following figure shows a sample of Maths coordinate.
Program JKM186-0 is a sample program that transform Maths coordinate to GraphicsWindow coordinate with a subroutine Map().
' Maths Coordiante Sample
' Copyright © 2019 Nonki Takahashi. The MIT License.
' Last update 2019-12-29
' Program ID JKM186-0
GraphicsWindow.Title = "Maths Coordinate Sample"
Init()
DrawGrid()
GraphicsWindow.PenColor = c2
While "True"
AddCircle()
Remove()
AddParabola()
Remove()
AddSin()
Remove()
AddCos()
Remove()
EndWhile
Sub AddCos
For x = xMin To xMax Step 0.1
y = Math.Cos(x)
Map()
If xMin < x Then
n = n + 1
shp[n] = Shapes.AddLine(_gx, _gy, gx, gy)
EndIf
_gx = gx
_gy = gy
EndFor
n = n + 1
shp[n] = Shapes.AddText("y = cos x")
Shapes.Move(shp[n], 10, 10)
EndSub
Sub AddCircle
For a = 0 To 360 Step 5
_a = Math.GetRadians(a)
x = Math.Cos(_a)
y = Math.Sin(_a)
Map()
If 0 < a Then
n = n + 1
shp[n] = Shapes.AddLine(_gx, _gy, gx, gy)
EndIf
_gx = gx
_gy = gy
EndFor
n = n + 1
shp[n] = Shapes.AddText("x² + y² = 1")
Shapes.Move(shp[n], 10, 10)
EndSub
Sub AddParabola
For x = -1.6 To 1.6 Step 0.1
y = Math.Power(x, 2)
Map()
If -1.6 < x Then
n = n + 1
shp[n] = Shapes.AddLine(_gx, _gy, gx, gy)
EndIf
_gx = gx
_gy = gy
EndFor
n = n + 1
shp[n] = Shapes.AddText("y = x²")
Shapes.Move(shp[n], 10, 10)
EndSub
Sub AddSin
For x = xMin To xMax Step 0.1
y = Math.Sin(x)
Map()
If xMin < x Then
n = n + 1
shp[n] = Shapes.AddLine(_gx, _gy, gx, gy)
EndIf
_gx = gx
_gy = gy
EndFor
n = n + 1
shp[n] = Shapes.AddText("y = sin x")
Shapes.Move(shp[n], 10, 10)
EndSub
Sub DrawGrid
GraphicsWindow.BrushColor = c2
GraphicsWindow.FontName = "Arial"
GraphicsWindow.FontSize = 14
For x = xMin To xMax Step 0.1
Map()
If x = 0 Then
pc = c2
GraphicsWindow.DrawText(gx, gh / 2, Math.Round(x))
ElseIf Math.Remainder(x, 1) = 0 Then
pc = c1
If x <> 3 Then
GraphicsWindow.DrawText(gx, gh / 2, Math.Round(x))
EndIf
Else
pc = c0
EndIf
GraphicsWindow.PenColor = pc
GraphicsWindow.DrawLine(gx, 0, gx, gh)
EndFor
For y = yMin To yMax Step 0.1
Map()
If y = 0 Then
pc = c2
GraphicsWindow.DrawText(gw / 2, gy, Math.Round(y))
ElseIf Math.Remainder(y, 1) = 0 Then
pc = c1
GraphicsWindow.DrawText(gw / 2, gy, Math.Round(y))
Else
pc = c0
EndIf
GraphicsWindow.PenColor = pc
GraphicsWindow.DrawLine(0, gy, gw, gy)
EndFor
GraphicsWindow.PenColor = c2
GraphicsWindow.DrawLine(gw - 10, gh / 2 - 4, gw, gh / 2)
GraphicsWindow.DrawLine(gw - 10, gh / 2 + 4, gw, gh / 2)
GraphicsWindow.DrawText(gw - 20, gh / 2, "x")
GraphicsWindow.DrawLine(gw / 2, 0, gw / 2 - 4, 10)
GraphicsWindow.DrawLine(gw / 2, 0, gw / 2 + 4, 10)
GraphicsWindow.DrawText(gw / 2, 10, "y")
EndSub
Sub Init
c2 = "#FF666666"
c1 = "#660099CC"
c0 = "#330099CC"
gw = 640
gh = 480
GraphicsWindow.Width = gw
GraphicsWindow.Height = gh
xMin = -3.2
xMax = 3.2
yMin = -2.4
yMax = 2.4
scale = 100
gxOffset = gw / 2
gyOffset = gh / 2
EndSub
Sub Map
gx = scale * x + gxOffset
gy = -scale * y + gyOffset
EndSub
Sub Remove
Program.Delay(3000)
For i = 1 To n
Shapes.Remove(shp[i])
EndFor
n = 0
EndSub
See Also
- [[articles:Wiki: Small Basic Portal]]
- [[articles:Small Basic: GraphicsWindow Basics]]
- [[articles:Small Basic Getting Started Guide: Chapter 6: Beginning Graphics]]