Small Basic: Rotation Centers for Shapes of Triangle and Line
In Small Basic program language, Shapes object has Rotate operation. Rotation centers for Rectangle and Ellipse are the centers of the shapes. But for Triangle and Line, the rotation centers are not always the centers of the shape. This article explains about the rotation centers for Triangle and Line. And this article is only for local program (compiled in Small Basic IDE).
Definition Co-ordinate for Triangle and Line
Rectangle and Ellipse don't have positions but have their sizes. Triangle and Line are defined as follows with co-ordinate of points.
- Shapes.AddTriangle(x1, y1, x2, y2, x3, y3)
- Shapes.AddLine(x1, y1, x2, y2)
These co-ordinate affect to determine the center of rotation. Most typical rule is that a rotation center is not negative in definition co-ordinate. It is always positive or zero.
Patterns with Sample Programs
Following programs calculate rotation centers and show them as red crosses. The usage of this program is to click to define vertices for triangle or end points for line.
- Rotate Triangle 0.1 (CNM748) - sample program for rotating triangle shape
- Rotate Line 0.1 (KSL776) - sample program for rotating line shape
Center of Circumscribed Rectangle of the Shape
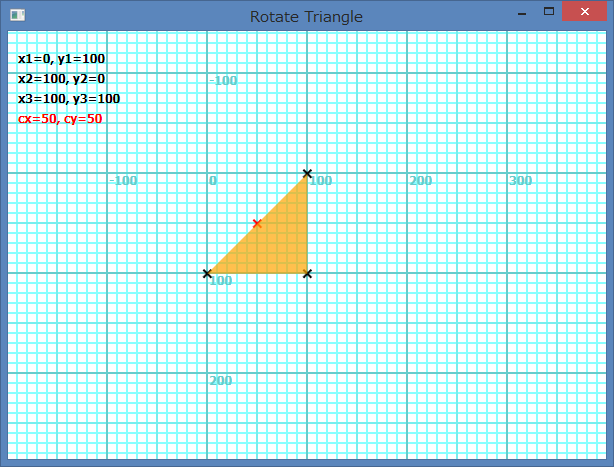
If the all vertices are not negative including zeros for each x and y in definition co-ordinate, the rotation center of the shape is the center of circumscribed rectangle of the shape. Following picture shows the case of Shapes.AddTriangle(0, 100, 100, 0, 100, 100). The rotation center becomes (50, 50).
Center of Circumscribed Rectangle of the Shape and the Origin
If the all vertices are not negative including no or one zero for x or y in definition co-ordinate, the rotation center of the shape is the center of circumscribed rectangle of the shape and the origin of definition co-ordinate. Following picture shows the case of Shapes.AddTriangle(50, 150, 150, 50, 150, 150). The rotation center becomes (75, 75).
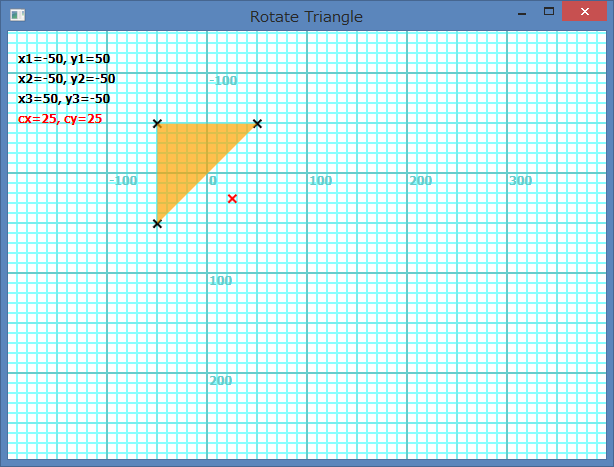
If the vertices have positive and negative in definition co-ordinate, the rotation center of the shape is the center of the rectangle which is a positive part of the circumscribed rectangle of the shape of definition co-ordinate. Following picture shows the case of Shapes.AddTriangle(-50, 50, -50, -50, 50, -50). The rotation center becomes (25, 25).
Origin of the Defined Shape
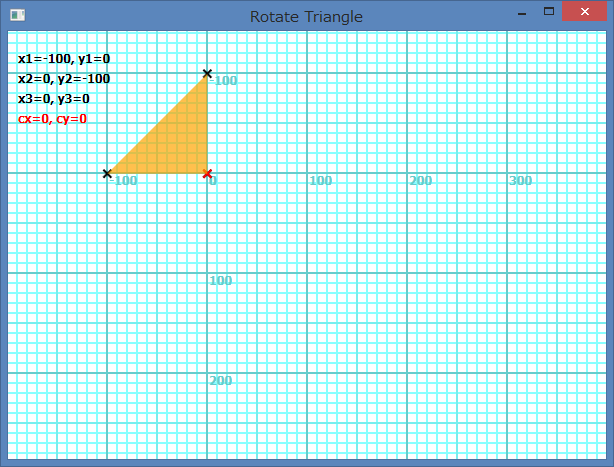
If the all vertices are negative or zero in definition co-ordinate, the rotation center of the shape is the origin of definition co-ordinate. Following picture shows the case of Shapes.AddTriangle(100, 0, 0, 100, 0, 0). The rotation center becomes (0, 0).
On X-Axis or Y-Axis
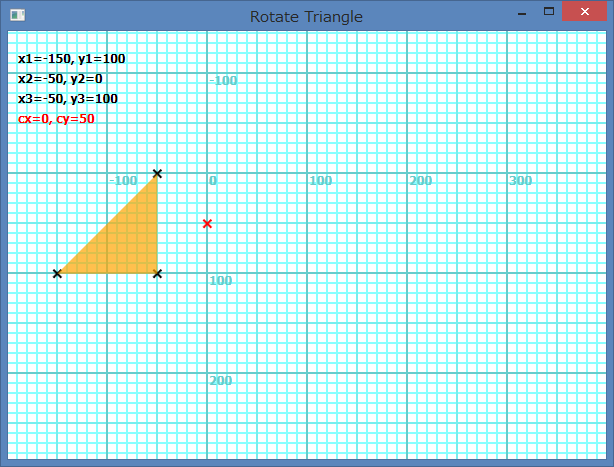
If the all vertices are not negative in x or y definition co-ordinate, the rotation center of the shape is on x-axis or y-axis. Following picture shows the case of Shapes.AddTriangle(-150, 100, -50, 0, -50, 100). The rotation center becomes (0, 50).
See Also
- Small Basic: How to Rotate a Shape Not from the Center (about Rectangle and Ellipse)
- Small Basic Known Issue: 27122 - Shapes.Rotate() Rotates Triangle and Line at Center in Local But at Corner in Remote