T-SQL: Relational Division
This article discusses one of the problems of relational algebra which was brought up in this Transact-SQL MSDN Forum T-sql - finding all sales orders that have similar products.
Introduction
There are certain kinds of problems in relational databases which may be solved using principals from Relational Division. There are many articles about Relational Division or Relational Algebra. Here is a list of a few very interesting articles Divided We Stand: The SQL of Relational Division by Celko and Relational division and Relationally Divided over EAV by Peter Larsson and readers may want to take a look at them and other articles on this topic.
Problem Definition
In the aforementioned thread the topic starter first wanted to find all orders that have similar products. He provided the table definition along with few rows of data.
Rather than using data from that thread let's consider the same problem but using AdventureWorks database instead. First let's see a solution for the problem of finding orders that have the same products.
Solutions
This problem has several solutions. First two are the true relational division solutions and the last solution is non-portable T-SQL only solution based on the de-normalization of the table. The first solution in that script was suggested by Peter Larsson after I asked him to check this article. I'll post the script I ran to compare all three solutions:
USE AdventureWorks2012;
SET NOCOUNT ON;
SET STATISTICS IO ON;
SET STATISTICS TIME ON;
PRINT 'PESO Solution';
SELECT t1.SalesOrderID AS OrderID
,t2.SalesOrderID AS SimilarOrderID
FROM (
SELECT SalesOrderID
,COUNT(*) AS Items
,MIN(ProductID) AS minProdID
,MAX(ProductID) AS maxProdID
FROM Sales.SalesOrderDetail
GROUP BY SalesOrderID
) AS v
INNER JOIN Sales.SalesOrderDetail AS t1 ON t1.SalesOrderID = v.SalesOrderID
INNER JOIN Sales.SalesOrderDetail AS t2 ON t2.ProductID = t1.ProductID
AND t2.SalesOrderID > t1.SalesOrderID
INNER JOIN (
SELECT SalesOrderID
,COUNT(*) AS Items
,MIN(ProductID) AS minProdID
,MAX(ProductID) AS maxProdID
FROM Sales.SalesOrderDetail
GROUP BY SalesOrderID
) AS w ON w.SalesOrderID = t2.SalesOrderID
WHERE w.minProdID = v.minProdID
AND w.maxProdID = v.maxProdID
AND w.Items = v.Items
GROUP BY t1.SalesOrderID
,t2.SalesOrderID
HAVING COUNT(*) = MIN(v.Items);
PRINT 'Common Relational Division /CELKO/Naomi solution';
SELECT O1.SalesOrderId AS OrderID
,O2.SalesOrderID AS SimilarOrderID
FROM Sales.SalesOrderDetail O1
INNER JOIN Sales.SalesOrderDetail O2 ON O1.ProductID = O2.ProductID
AND O1.SalesOrderID < O2.SalesOrderID
GROUP BY O1.SalesOrderID
,O2.SalesOrderID
HAVING COUNT(O1.ProductID) = (
SELECT COUNT(ProductID)
FROM Sales.SalesOrderDetail SD1
WHERE SD1.SalesOrderID = O1.SalesOrderID
)
AND COUNT(O2.ProductID) = (
SELECT COUNT(ProductID)
FROM Sales.SalesOrderDetail SD2
WHERE SD2.SalesOrderID = O2.SalesOrderID
);
PRINT 'XML PATH de-normalization solution';
WITH cte
AS (
SELECT SalesOrderID
,STUFF((
SELECT ', ' + CAST(ProductID AS VARCHAR(30))
FROM Sales.SalesOrderDetail SD1
WHERE SD1.SalesOrderID = SD.SalesOrderID
ORDER BY ProductID
FOR XML PATH('')
), 1, 2, '') AS Products
FROM Sales.SalesOrderDetail SD
GROUP BY SD.SalesOrderID
)
SELECT cte.SalesOrderID AS OrderID
,cte1.SalesOrderID AS SimilarOrderID
,cte.Products
FROM cte
INNER JOIN cte AS cte1 ON cte.SalesOrderID < cte1.SalesOrderID
AND cte.Products = cte1.Products;
SET STATISTICS IO OFF;
First solution JOINS with the number of items in each order and MIN/MAX product in each order. This solution is based on the idea Peter proposed in this closed MS Connect Item Move T-SQL language closer to completion with a DIVIDE BY operator.
The second solution self-joins the table based on the ProductID using an extra condition of O1.OrderID < O2.Order2 (we're using < instead of <> in order to avoid opposite combinations), then groups by both OrderID columns and uses HAVING clause to make sure the number of products is the same as the number of products in each individual order. This HAVING idea is very typical for the Relational Division problem.
Interestingly, the number of combinations in AdventureWorks database is 1,062, 238 (more than rows in the SalesOrderDetail table itself). This is due to the fact that many orders consist of only single product.
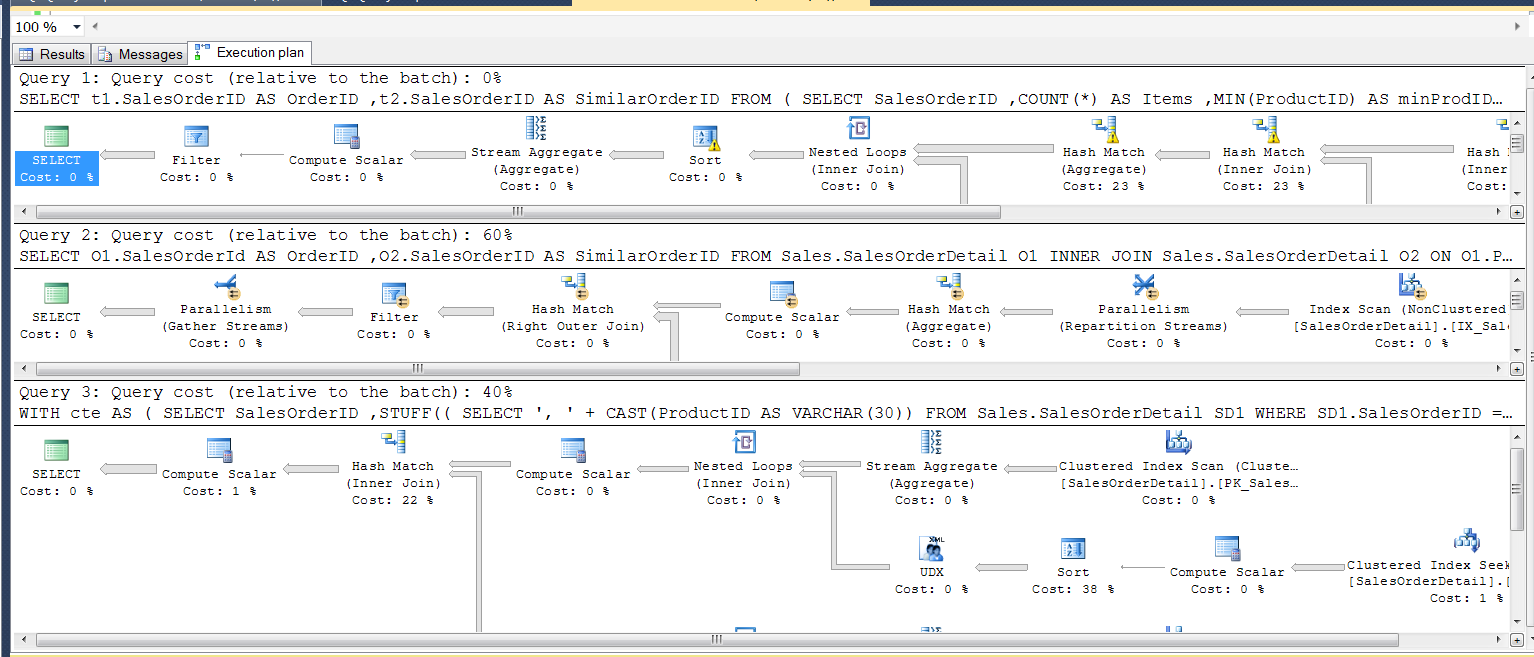
The last solution is rather straightforward and uses XML PATH approach to get all products in one row for each order ID, then self-joins based on this new Products column. This solution is not portable into other relational database languages but specific for T-SQL only. Interestingly, it performs better than second 'true' Relational Division solution as you can see in this picture.
As you can see, the first query takes 0%, second 60% while the last takes 40% of the execution time.
The last solution, however, is also not very flexible and is only suitable for finding exact matches.
These are results I got on SQL Server 2012 SP1 64 bit (they are much better on SQL Server 2014 CTP according to Peter):
PESO Solution
Table 'SalesOrderDetail'. Scan count 3410626, logical reads 7265595, physical reads 0, read-ahead reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0.
Table 'Worktable'. Scan count 855922, logical reads 3462746, physical reads 0, read-ahead reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0.
SQL Server Execution Times:
CPU time = 35272 ms, elapsed time = 114920 ms.
Common Relational Division /CELKO/Naomi solution
Table 'SalesOrderDetail'. Scan count 36, logical reads 3292, physical reads 0, read-ahead reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0.
Table 'Worktable'. Scan count 266, logical reads 907592, physical reads 0, read-ahead reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0.
SQL Server Execution Times:
CPU time = 478703 ms, elapsed time = 214748 ms.
XML PATH de-normalization solution
Table 'Worktable'. Scan count 0, logical reads 12971, physical reads 0, read-ahead reads 0, lob logical reads 8764, lob physical reads 0, lob read-ahead reads 0.
Table 'SalesOrderDetail'. Scan count 62932, logical reads 194266, physical reads 0, read-ahead reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0.
SQL Server Execution Times:
CPU time = 5054 ms, elapsed time = 14069 ms.
Best Exact Match Solution
Peter sent yet another variation of the solution for the integer Product ID (this solution will not work if the product ID /Item ID uses character or GUID key).
SELECT v.SalesOrderID AS OrderID,
w.SalesOrderID AS SimilarOrderID,
v.Items
FROM (
SELECT SalesOrderID,
COUNT(ProductID) AS Items,
MIN(ProductID) AS minProdID,
MAX(ProductID) AS maxProdID,
SUM(ProductID) AS sumProdID,
CHECKSUM_AGG(10000 * ProductID) AS cs
FROM Sales.SalesOrderDetail
GROUP BY SalesOrderID
) AS v
INNER JOIN (
SELECT SalesOrderID,
COUNT(ProductID) AS Items,
MIN(ProductID) AS minProdID,
MAX(ProductID) AS maxProdID,
SUM(ProductID) AS sumProdID,
CHECKSUM_AGG(10000 * ProductID) AS cs
FROM Sales.SalesOrderDetail
GROUP BY SalesOrderID
) AS w ON w.Items = v.Items
AND w.minProdID = v.minProdID
AND w.maxProdID = v.maxProdID
AND w.cs = v.cs
AND w.sumProdID = v.sumProdID
WHERE w.SalesOrderID > v.SalesOrderID
This solution joins 2 aggregate information together based on CHECKSUM_AGG function. By checking all these aggregate functions it is enough to conclude if the orders consist of the same products or not. This is the simplest and ingenious query and it performs the best among the other variations I tried. The limitation of this query is that it assumes integer key for the product id.
I got the following results for this solution:
Table 'Worktable'. Scan count 0, logical reads 0, physical reads 0, read-ahead reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0.
Table 'SalesOrderDetail'. Scan count 2, logical reads 2492, physical reads 0, read-ahead reads 0, lob logical reads 0, lob physical reads 0, lob read-ahead reads 0.
SQL Server Execution Times:
CPU time = 562 ms, elapsed time = 9791 ms.
Slight Variation of the Original Problem
In that thread the topic starter also wanted to compare orders based on partial similarity. You may recognize this problem as 'Customers who bought this item also bought...' as you often can see in different websites.
Say, we want to find orders, that have 2/3 or more of the products matching. We will only consider orders with more than 2 items (3 and up) for this problem. The first solution can be easily adjusted for this new problem:
;
WITH cte
AS (
SELECT SalesOrderID
,ProductID
,COUNT(ProductID) OVER (PARTITION BY SalesOrderID) AS ProductsCount
FROM Sales.SalesOrderDetail
)
SELECT O1.SalesOrderId AS OrderID
,O2.SalesOrderID AS SimilarOrderID
FROM cte O1
INNER JOIN cte O2 ON O1.ProductID = O2.ProductID
AND O1.SalesOrderID < O2.SalesOrderID
WHERE O1.ProductsCount > = 3
AND O2.ProductsCount >= 3
GROUP BY O1.SalesOrderID
,O2.SalesOrderID
HAVING COUNT(O1.ProductID) >= (
(
SELECT COUNT(ProductID)
FROM Sales.SalesOrderDetail SD1
WHERE SD1.SalesOrderID = O1.SalesOrderID
) * 2.0
) / 3.0
AND COUNT(O2.ProductID) >= (
(
SELECT COUNT(ProductID)
FROM Sales.SalesOrderDetail SD2
WHERE SD2.SalesOrderID = O2.SalesOrderID
) * 2.0
) / 3.0
ORDER BY OrderID
,SimilarOrderID;
We can verify our results back for the few first rows:
SELECT SalesOrderID
,stuff((
SELECT ', ' + cast(ProductID AS VARCHAR(30))
FROM Sales.SalesOrderDetail SD1
WHERE SD1.SalesOrderID = SD.SalesOrderID
ORDER BY ProductID
FOR XML PATH('')
), 1, 2, '') AS Products
FROM Sales.SalesOrderDetail SD
WHERE SalesOrderID IN (
43659
,43913,
43659, 44528,
43659, 44566,
43659, 44761,
43659, 46077)
GROUP BY SalesOrderID
ORDER BY SalesOrderID
I will show two variations of the solutions for the similar orders problem. While I am getting better reads for the second query, the execution time is much better for the first query:
SET STATISTICS TIME ON;
SET STATISTICS IO ON;
DECLARE @Percentage DECIMAL(10, 2);
SET @Percentage = 0.75;
WITH cte
AS (
SELECT SalesOrderID
,ProductID
,COUNT(ProductID) OVER (PARTITION BY SalesOrderID) AS ProductsCount
FROM Sales.SalesOrderDetail
)
SELECT O1.SalesOrderId AS OrderID
,O2.SalesOrderID AS SimilarOrderID
FROM cte O1
INNER JOIN cte O2 ON O1.ProductID = O2.ProductID
AND O1.SalesOrderID < O2.SalesOrderID
WHERE O1.ProductsCount > = 3
AND O2.ProductsCount >= 3
GROUP BY O1.SalesOrderID
,O2.SalesOrderID
HAVING COUNT(O1.ProductID) >= (
SELECT COUNT(ProductID)
FROM Sales.SalesOrderDetail SD1
WHERE SD1.SalesOrderID = O1.SalesOrderID
) * @Percentage
AND COUNT(O2.ProductID) >= (
SELECT COUNT(ProductID)
FROM Sales.SalesOrderDetail SD2
WHERE SD2.SalesOrderID = O2.SalesOrderID
) * @Percentage
ORDER BY OrderID
,SimilarOrderID;
WITH cte
AS (
SELECT SalesOrderID
,COUNT(ProductID) AS Items
FROM Sales.SalesOrderDetail
GROUP BY SalesOrderID
)
SELECT O1.SalesOrderId AS OrderID
,MIN(C1.Items) AS [Products 1]
,O2.SalesOrderID AS SimilarOrderID
,MIN(C2.Items) AS [Products 2]
FROM Sales.SalesOrderDetail O1
INNER JOIN cte C1 ON O1.SalesOrderID = C1.SalesOrderID
INNER JOIN Sales.SalesOrderDetail O2 ON O1.ProductID = O2.ProductID
AND O1.SalesOrderID < O2.SalesOrderID
INNER JOIN cte C2 ON O2.SalesOrderID = C2.SalesOrderID
GROUP BY O1.SalesOrderID
,O2.SalesOrderID
HAVING COUNT(*) >= MIN(C1.Items) * @Percentage
AND COUNT(*) >= MIN(C2.Items) * @Percentage
AND MIN(C1.Items)>=3 AND MIN(C2.Items) >=3
ORDER BY OrderID
,SimilarOrderID;
I will be interested in your results and ideas for this type of the query for partial (percentage) match.
Note from the Comments
I received the following comment from Andriy Zabavskyy:
We could significantly improve the first out of the latest two solutions extending the join condition by the following statement:
AND O1.ProductsCount between floor(O2.ProductsCount * @Percentage) and ceiling(O2.ProductsCount / @Percentage)
On my local machine it gives an improvement equal to about 2.5 times in terms of time execution.
I let the readers of this article to test this suggestion.
Conclusion
In this article I showed that some common relational division problems can be solved using set-based solutions. These solutions may not perform well, however, on the big datasets. I encourage the readers to provide their ideas for the listed problems and their Pros/Cons.
Credits
I want to thank Peter Larsson who reviewed this article and came up with several great solution ideas. I knew I can count on Peter!
See Also
This article participated in the TechNet Guru Contributions for December 2013 and won the Gold Prize.