Уроки программирования F#. Урок 2: Строим фрактальное изображение
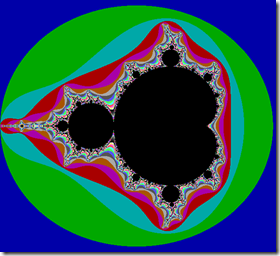
На прошлом уроке мы рассмотрели основные понятия функционального программирования, теперь давайте попробуем применить их на практике. Поскольку функциональное программирование, как вы наверное поняли, идеально подходит для решения математических задач, то рассмотрим именно такую задачу – построение изображения множества Мандельброта, самого известного фрактального множества, вот такого:
Математически, множество Мандельброта определяется следующим образом. Рассмотрим последовательность комплексных чисел z(n+1) = z(n)^2+c, z(0)=0. Для различных c эта последовательность либо сходится, либо расходится Например, для c=0 z(i) = 0, а для c=2 имеем расходящуюся последовательность. Так вот, множество Мандельброта – это множество тех c, для которых последовательность сходится.
Переходим к реализации алгоритма на F#. Для начала, определим исходную функцию
let mandelf (c:Complex) (z:Complex) = z*z+c;;
Здесь нам пришлось в явном виде указать тип Complex (это надо сделать хотя бы для одной из переменных, но мы для симметрии сделали для двух), поскольку по умолчанию для операции + полагается целый тип. Для того, чтобы тип Complex стал доступен, в начале придется указать преамбулу:
open Microsoft.FSharp.Math;;
open System;
Чтобы проверить сходимость, мы примем небольшое допущение. Будем считать, что последователность сходится, если |z(20)|<1. Для вычисления z(20) используем следующую функцию многократной композиции, рекурсивно применяющую указанную функцию заданное число раз:
let rec rpt n f =
if n=0 then (fun x->x)
else f >> (rpt (n-1) f);;
Здесь знак >> обозначает композицию функций, а запись fun x->x – тождественную функцию. Вообще говоря, конструкция fun x –> …. позволяет нам задать функциональную константу, т.е. выражение типа функции от одного аргумента. Например, следующие две конструкции – эквивалентны:
let double x = x*2
let double = fun x -> x*2
В нашем случае функция rpt принимает один аргумент целого типа n (число повторений), и некоторую функцию f, т.е. имеет тип rpt : int -> ('a -> 'a) -> ('a -> 'a). Для n=0 возвращается тождественная функция, а для n>0 – композиция f и (n-1)-кратного применения f.
Возврящаясь к нашей задаче, вспомним, что для фиксированного c частичное применение каррированной функции (mandelf c) будет функцией одного аргумента (x), и применим к этой функции функцию многократной композиции. В результате, |z(20)| вычислится как rpt 20 (mandelf c) (Complex.zero). Действительно, rpt 20 (mandelf c) будет обозначать 20-кратное применение функции mandelf с, которое затем мы применяем к 0. Тогда функция принадлежности комплексного числа к множеству Мандельброта запишется как
let ismandel c = Complex.Abs(rpt 20 (mandelf c) (Complex.zero))<1.0;;
Остальное – дело техники. Определяем функцию масштабирования scale (она будет в качестве аргументов брать пары чисел – диапазоны изменения переменных типа float*float и int*int), и в двойном цикле печатаем множество на консоли:
let scale (x:float,y:float) (u,v) n = float(n-u)/float(v-u)*(y-x)+x;;
for i = 1 to 60 do
for j = 1 to 60 do
let lscale = scale (-1.2,1.2) (1,60) in
let t = complex (lscale j) (lscale i) in
System.Console.Write(if ismandel t then "*" else " ");
System.Console.WriteLine("")
;;
Но это ещё не всё! Вспомним, что программисту на F# доступна вся мощь платформы Microsoft.NET! Поэтому мы можем построить графическое изображение в окне, используя Windows Forms и библиотеку System.Drawing! Соответствующий код:
#light
open System.Drawing
open System.Windows.Forms
let form =
let image = new Bitmap(400, 400)
let lscale = scale (-1.2,1.2) (0,image.Height-1)
for i = 0 to (image.Height-1) do
for j = 0 to (image.Width-1) do
let t = complex (lscale i) (lscale j) in
image.SetPixel(i,j,if ismandel t then Color.Black else Color.White)
let temp = new Form()
temp.Paint.Add(fun e -> e.Graphics.DrawImage(image, 0, 0))
temp
[<STAThread>]
do Application.Run(form);;
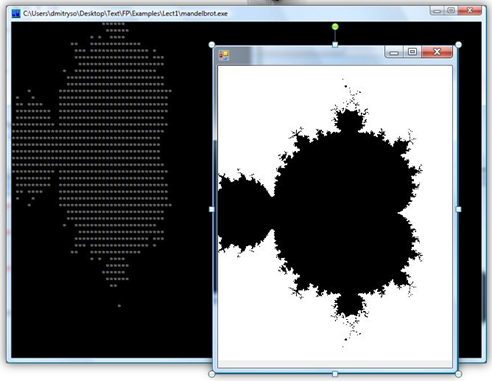
Что из этого получилось – см. на картинке ниже:
Конечно, для получения полноценного цветного изображения множества Мандельброта на F# надо ещё немного поработать! Предоставляю моим читателям сделать это в качестве упражнения. Если получится – пишите в комментариях, мне всегда приятно читать о ваших успехах!
Comments
Anonymous
May 21, 2009
Столько for и if в коде очень сильно смущает..., ну не того хочется от ФЯAnonymous
May 28, 2009
вот чистый вариант без for и if. работает гдето на 10% быстрее :) let rec nrpt f x = function | 0 -> x | n -> nrpt f (f x) (n - 1) let mandelf c z = z * z + c let ismandel c = Complex.Abs (nrpt (mandelf c) Complex.zero 20) < 1.0 let colmandel = function true -> Color.Black | _ -> Color.White let scale (x,y) (u,v) n = float(n - u) / float(v - u) * (y - x) + x let form = let image = new Bitmap(400, 400) let lscale = scale (-1.2, 1.2) (0, image.Height-1) let rec filler = function | -1 , _ -> () | y , -1 -> filler (y - 1, (image.Width - 1)) | y , x -> let t = complex (lscale y) (lscale x) image.SetPixel ( y, x, t |> ismandel |> colmandel ) filler (y, x - 1) filler (image.Height - 1, image.Width - 1) let temp = new Form(Width = 410, Height = 410) temp.Paint.Add(fun e -> e.Graphics.DrawImage (image, 0, 0)) tempAnonymous
April 11, 2011
stdin(6,23): error FS0039: Значение, конструктор, пространство имен или тип "complex" не определеноAnonymous
April 12, 2011
Необходимо подключить к проекту FSharp.PowerPack.dll которая в ходит в PowerPack fsharppowerpack.codeplex.com