GPGPU and x64 Multicore Programming with Accelerator from F#
Microsoft recently released a preview of the Accelerator V2 GPU and x64 multicore programming system on Microsoft Connect. This system provides a civilized level of abstraction for writing data-parallel programs that execute on GPUs and multicore processors. An experimental FPGA target is under development.
Even on my low end graphics card I get pretty impressive performance results for the 2D convolver that is described in this blog. All 8 cores of my 64-bit Windows 7 workstation are also effectively exercised by the x64 multicore target, which exploits SIMD processor instructions and multithreading. I won't say anything about performance in this blog post since what I want to focus on is how to use Accelerator from the F# functional programming language. We will work backwards by starting off with a complete implementation of a two dimensional convolver. Step by step we show how this convolver is expressed using Accelerator from F#.
First here is the beautiful implementation of a two dimensional convolver. The rest of this post explains why this code works.
open System
open Microsoft.ParallelArrays
[<EntryPoint>]
let main(args) =
// Declare a filter kernel for the convolution
let testKernel = Array.map float32 [| 2; 5; 7; 4; 3 |]
// Specify the size of each dimension of the input array
let inputSize = 10
// Create a pseudo-random number generator
let random = Random (42)
// Declare a psueduo-input data array
let testData = Array2D.init inputSize inputSize (fun i j -> float32 (random.NextDouble() *
float (random.Next(1, 100))))
// Create an Accelerator float parallel array for the F# input array
use testArray = new FloatParallelArray(testData)
// Declare a function to convolve in the X or Y direction
let rec convolve (shifts : int -> int []) (kernel : float32 []) i (a : FloatParallelArray)
= let e = kernel.[i] * ParallelArrays.Shift(a, shifts i)
if i = 0 then
e
else
e + convolve shifts kernel (i-1) a
// Declare a 2D convolver
let convolveXY kernel input
= // First convolve in the X direction and then in the Y direction
let convolveX = convolve (fun i -> [| -i; 0 |]) kernel (kernel.Length - 1) input
let convolveY = convolve (fun i -> [| 0; -i |]) kernel (kernel.Length - 1) convolveX
convolveY
// Create a DX9 target and use it to convolve the test input
use dx9Target = new DX9Target()
let convolveDX9 = dx9Target.ToArray2D (convolveXY testKernel testArray)
printfn "DX9: -> \r\n%A" convolveDX9
// Create a X64 multi-core target and use it to convolve the test input
use x64MCTarget = new X64MulticoreTarget()
let convolveMC = x64MCTarget.ToArray2D (convolveXY testKernel testArray)
printfn "MC: -> \r\n%A" convolveMC
0
This program sets up a pseudo-random two dimensional input array, declares a two dimensional convolver and then uses two of the targets supported by Accelerator to convolve the input array. The first target uses a GPU to perform the convolution and the second target uses multiple x64 processor cores and makes use of special SIMD instructions. When this program is run it produces the following output:
DX9: ->
[[4124.88916f; 4006.17432f; 3619.18579f; 4345.93262f; 6214.79004f; 7851.854f;
6639.24854f; 6447.55664f; 4849.12109f; 5399.95215f]
[3999.14282f; 3891.52783f; 3691.94263f; 4562.6543f; 6413.09766f; 7815.42236f;
6846.51172f; 6543.7251f; 4950.29443f; 5539.11377f]
[4643.48877f; 4448.87451f; 4293.98975f; 4958.56201f; 6505.2334f; 7420.50586f;
7069.68311f; 6669.47803f; 5239.27148f; 5991.7793f]
[5392.69336f; 5102.70215f; 4892.03027f; 5074.26025f; 5990.81055f; 6369.36475f;
6808.10986f; 6476.23047f; 5292.99463f; 6154.81885f]
[8989.50488f; 8397.94434f; 7150.7959f; 5570.37061f; 5170.64307f; 5217.95703f;
6137.8042f; 6353.71484f; 5624.02979f; 6247.72852f]
[12248.4824f; 11455.2373f; 9597.80078f; 6825.54688f; 5358.00586f; 4921.00293f;
6604.14258f; 7520.95361f; 7361.63232f; 7363.42578f]
[16833.0352f; 15605.6055f; 12528.748f; 8065.896f; 5745.88574f; 5093.6792f;
7391.62354f; 9219.54004f; 9945.78711f; 9624.86328f]
[13102.8984f; 12436.5234f; 10673.6123f; 7992.61035f; 6201.81299f; 5618.32861f;
7226.84521f; 9439.95508f; 10573.7754f; 10420.5703f]
[14555.6426f; 14135.1074f; 12600.9141f; 10219.6904f; 8211.8623f; 7361.39746f;
7424.83643f; 9536.95605f; 10884.3418f; 10907.2549f]
[10885.0293f; 11083.6436f; 11301.6055f; 11469.3613f; 10785.7178f; 10094.2041f;
9660.19238f; 11580.3281f; 12738.5098f; 12256.5371f]]
MC: ->
[[4124.88965f; 4006.17529f; 3619.18652f; 4345.93311f; 6214.79053f; 7851.85449f;
6639.24902f; 6447.55664f; 4849.12109f; 5399.95215f]
[3999.14282f; 3891.52783f; 3691.94263f; 4562.6543f; 6413.09814f; 7815.42236f;
6846.51172f; 6543.7251f; 4950.29443f; 5539.11377f]
[4643.48877f; 4448.87451f; 4293.98975f; 4958.56201f; 6505.23389f; 7420.50586f;
7069.68311f; 6669.47803f; 5239.27148f; 5991.7793f]
[5392.69336f; 5102.70215f; 4892.03027f; 5074.26074f; 5990.81152f; 6369.36523f;
6808.10986f; 6476.23047f; 5292.99463f; 6154.81934f]
[8989.50488f; 8397.94434f; 7150.7959f; 5570.37061f; 5170.64307f; 5217.95752f;
6137.80469f; 6353.71484f; 5624.03027f; 6247.72852f]
[12248.4844f; 11455.2383f; 9597.80078f; 6825.54785f; 5358.00586f; 4921.00293f;
6604.14355f; 7520.95459f; 7361.63232f; 7363.42627f]
[16833.0352f; 15605.6055f; 12528.748f; 8065.896f; 5745.88574f; 5093.67969f;
7391.62354f; 9219.54004f; 9945.78906f; 9624.86328f]
[13102.8984f; 12436.5234f; 10673.6133f; 7992.61084f; 6201.81348f; 5618.3291f;
7226.84521f; 9439.95605f; 10573.7754f; 10420.5713f]
[14555.6426f; 14135.1074f; 12600.916f; 10219.6914f; 8211.86328f; 7361.39795f;
7424.83643f; 9536.95703f; 10884.3418f; 10907.2559f]
[10885.0293f; 11083.6445f; 11301.6074f; 11469.3633f; 10785.7188f; 10094.2051f;
9660.19336f; 11580.3281f; 12738.5107f; 12256.5371f]]
A convolver computes a weighted average around some point. Image editing programs typically have an operation that smoothes an image and this is usually performed by a two dimensional convolution around each pixel. We shall discuss how to implement a one dimensional (1D) convolver fist and then generalize this to a two dimensional (2D) convolver afterwards. A convolution in one dimension can be expressed as a weighted sum around each value in an input array (or stream):
Here is a concrete example of a one dimensional convolution of an eight element array x which is being convolved by a five element filter kernel a to produce an eight element result array y. The filter kernel a appears to be like a window which slides across each element of the input array. To simplify the explanation and code, the filter is placed to the left of the element being convolved. A more realistic convolver would centre the filter kernel over the element being convolved but that introduces some extra boundary condition code which I don’t want to get bogged down with in this blog.
We can implement a 1D software convolver in F# as follows:
let clamp i (input : float32 [])
= if i < 0 then
input.[0]
else
input.[i]
let convolveAt i (kernel : float32 []) input
= Array.sum [| for k in 0 .. kernel.Length - 1 -> clamp (i-k) input * kernel.[k] |]
let softwareConvolver kernel (input : float32 [])
= [| for i in 0 .. input.Length - 1 -> convolveAt i kernel input |]
The clamp function has the following type which accepts an array index of type int and an array of float32 values and returns an element of the array or a clamped value.
val clamp : int -> float32 [] -> float32
This function allows us to define values for negative array indices and works by returning the value of the first array element input.[0] whenever we try to compute a negative index of the input array. Note that in F# arrays are indexed with the .[...] notation.
The convolveAt function has the type:
val convolveAt : int -> float32 [] -> float32 [] -> float32
and computes the convolution of a single position in the input array to produce the result at the corresponding output array. For example, the picture above illustrates the calculation of:
convolveAt 5 [| 2; 5; 7; 4; 3 |] [| 7; 2; 5; 9; 3; 8; 6; 4 |]
Note that array literals in F# are written using [| ... |] brackets. The definition of convolveAt makes use of an array comprehension which allows us to specify an expression that defines the values of an array:
[| for k in 0 .. kernel.Length - 1 -> clamp (i-k) input * kernel.[k] |]
If the value of kernel.Length is 5 and if we are convolving at the first array index value of 0 for i then this is equivalent to writing:
[| clamp (- 4) input * kernel.[4] ;
clamp (- 3) input * kernel.[3] ;
clamp (- 2) input * kernel.[2] ;
clamp (- 1) input * kernel.[1] ;
clamp 0 input * kernel.[0] ;
|]
The final step is to sum the elements of this array which is accomplished with a call to the Array.sum library function.
We can also exploit an array comprehension to produce the completely convolved result array by applying the single point convolution function to every element of the array by using the software function which has the type:
val softwareConvolver : float32 [] -> float32 [] -> float32 []
and the definition:
let softwareConvolver kernel (input : float32 [])
= [| for i in 0 .. input.Length - 1 -> convolveAt i kernel input |]
Although this code correctly implements a 1D convolver it is not an ideal starting point for a parallel implementation of convolution. To make an efficient implementation of the convolver for Accelerator we have to express the computation avoiding the manipulation of absolute array indices. Instead we should try to think in terms of whole array operations and relative array indices. The first step in this direction is to think about how to compute the whole result array y rather than how to compute an individual element y[i]. That is, we wish to compute an array which has the following form:
y = [y[0], y[1], y[2], y[3], y[4], y[5], y[6], y[7]]
Furthermore, we wish to define y using only whole array operations. To help spot how we should do this the equations for y are expanded:
y[0] = a[0]x[0] + a[1]x[-1] + a[2]x[-2] + a[3]x[-3] + a[4]x[-4]
y[1] = a[0]x[1] + a[1]x[0] + a[2]x[-1] + a[3]x[-2] + a[4]x[-3]
y[2] = a[0]x[2] + a[1]x[1] + a[2]x[0] + a[3]x[-1] + a[4]x[-2]
y[3] = a[0]x[3] + a[1]x[2] + a[2]x[1] + a[3]x[0] + a[4]x[-1]
y[4] = a[0]x[4] + a[1]x[3] + a[2]x[2] + a[3]x[1] + a[4]x[0]
y[5] = a[0]x[5] + a[1]x[4] + a[2]x[3] + a[3]x[2] + a[4]x[1]
y[6] = a[0]x[6] + a[1]x[5] + a[2]x[4] + a[3]x[3] + a[4]x[2]
y[7] = a[0]x[7] + a[1]x[6] + a[2]x[5] + a[3]x[4] + a[4]x[3]
We need some way of expressing the result of y in terms of whole array operations on a or x or through the use of only relative indices i.e. we wish to avoid mentioning absolute indices. Notice that the computation above does have whole operations e.g. the second column on the left shows the whole of the x array (shifted left by one) is multiplied by the scalar value a[1]. The pattern occurs across all four columns with each column corresponding to one of the five coefficients. In each column the corresponding scalar coefficient value is used to multiply a shifted version of the x input. This observation allows us to express the value of y using only whole array operations on x and its shifted counterparts. The calculations below represent the x and y arrays as a vector. The multiplication corresponds to the multiplication of a vector by a scalar value. The addition corresponds to the addition of two vectors.
y = [y[0], y[1], y[2], y[3], y[4], y[5], y[6], y[7]]
= a[0] * [x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7]] +
a[1] * [x[-1], x[0], x[1], x[2], x[3], x[4], x[5], x[6]] +
a[2] * [x[-2], x[-1], x[0], x[1], x[2], x[3], x[4], x[5]] +
a[3] * [x[-3], x[-2], x[-1], x[0], x[1], x[2], x[3], x[4]] +
a[4] * [x[-4], x[-3], x[-2], x[-1], x[0], x[1], x[2], x[3]]
This representation is an improvement from the original representation because it contains vector multiplications and vector additions which can be performed in parallel. The original formulation contained multiplications of scalar values (i.e. an element of the coefficient array) by scalar values (e.g. an element of the input array). This representation is not directly amenable to a parallel implementation.
To make the nature of the data-parallel operation shown above clearer we introduce the shift operator which takes as input an array and an amount to shift by N and returns an array of the same size except all the elements are shifted up by the specified number of positions. The first N elements of the result array are clamped by filling them with the first element of the input array. Here are some examples of shifts:
shift (x, 0) = [7, 2, 5, 9, 3, 8, 6, 4] = x
shift (x, -1) = [7, 7, 2, 5, 9, 3, 8, 6]
shift (x, -2) = [7, 7, 7, 2, 5, 9, 3, 8]
Using the shift operator we can re-express y as:
y = a[0] * shift (x, 0) + a[1] * shift (x, -1) + a[2] * shift (x, -2) + a[3] * shift (x, -3) +
a[4] * shift (x, -4)
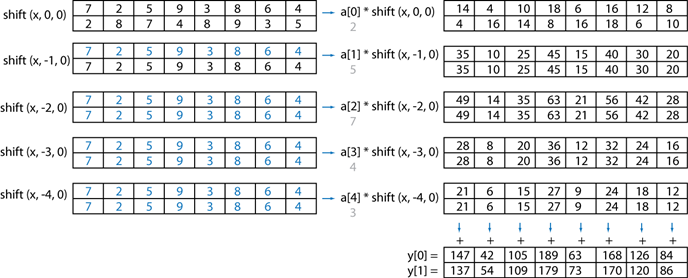
This leads to a data-parallel implementation which can perform each coefficient multiplication in parallel with the others followed by a sum in parallel. These parallel operations are described in the following figure.
Each blue arrow in this picture corresponds to a data-parallel operation. The F# program below shows how to implement this 1D convolution using both the DX9 GPU target and the x64 SIMD multi-core target.
open System
open Microsoft.ParallelArrays
[<EntryPoint>]
let main(args) =
// Declare an input data array
let inputData = Array.map float32 [| 7; 2; 5; 9; 3; 8; 6; 4 |]
// Declare filter kernel for the convolution
let kernel = Array.map float32 [| 2; 5; 7; 4; 3 |]
let kernelSize = Array.length kernel
// Create an Accelerator float parallel array for the F# input array
use inputArray = new FloatParallelArray(inputData)
// Build the expression
let rec expr i = let e = kernel.[i] *
ParallelArrays.Shift(inputArray, -i)
if i = 0 then
e
else
e + expr (i-1)
// Create DX9 target and compute result
use dx9Target = new DX9Target()
let resDX = dx9Target.ToArray1D(expr (kernelSize-1))
printfn "DX9 --> \r\n%A" resDX
// Create X64 multi-core target and compute result
use mc64Target = new X64MulticoreTarget()
let resMC = mc64Target.ToArray1D(expr (kernelSize-1))
printfn "X64MC --> \r\n%A" resMC
0
When run this produces the expected output:
DX9 -->
[|147.0f; 137.0f; 118.0f; 106.0f; 115.0f; 120.0f; 124.0f; 133.0f|]
X64MC -->
[|147.0f; 137.0f; 118.0f; 106.0f; 115.0f; 120.0f; 124.0f; 133.0f|]
To use an Accelerator target the input data must be created for an Accelerator data-parallel array. Typically the data represented by these arrays will be held in some memory specified by the target implementation. For example, for the DX9 GPU target the input values will be copied to memory on your graphics card. Accelerator provides several methods for creating data parallel arrays and here we create a floating point data-parallel array using a constructor:
new :: float32 [] -> FloatParallelArray
and the type of inputArray is FloatParallelArray .
In your F# program you should think of a FloatParallelArray as being a reference or a handle to some real array somewhere else. When you write computations over values of type FloatParallelArray what you are really doing is building up a symbolic expression tree that represents the computation that you want. When you try to evaluate such an expression the Accelerator system JITs (e.g. to GPU code via DX9) to produce the actual code for performing your computation and executes it with the data in the input data-parallel arrays and transmits the result back to your F# program.
Accelerator provides a library of data-parallel arrays and data-parallel operations over its data-parallel arrays. To perform a data-parallel multiplication of a data-parallel array by a single kernel coefficient we use one of Accelerator’s data-parallel multiplication operations (there are many other overloads):
val (*) : FloatParallelArray -> FloatParallelArray -> FloatParallelArray
This does not immediately perform the multiplication. What is really happening is that an expression tree is built up with a multiplication node in it. However, the JIT-ing nature of the Accelerator implementation almost makes it looks like the code is being executed immediately.
The addition operation used in the 1D convolver is also a data-parallel addition over FloatParallelArrays:
val (+) : FloatParallelArray -> FloatParallelArray -> FloatParallelArray
Finally, the shift operation here works over one dimensional arrays of type FloatParallelArray and takes just one number which specified how much to shift by:
val ParallelArrays.Shift : FloatParallelArray -> int -> FloatParallelArray
We may be tempted to specify the overall expression for the convolver by writing:
let convolver1D kernel input
= List.fold 0 [ for k in 0 .. kernel.Length - 1
-> kernel.[i] * ParallelArrays.Shift(inputArray, -i) ]
and how nice that would be but sadly we don’t have a proper 0 yet so instead we write a recursive formulation:
// Build the expression
let rec expr i = let e = kernel.[i] *
ParallelArrays.Shift(inputArray, -i)
if i = 0 then
e
else
e + expr (i-1)
where expr has the type:
val expr : int -> FloatParallelArray
Given the index of the highest element in the kernel this function builds up an expression which computes the 1D convolution. This expression is used to call the DX9 GPU target to perform the computation and retrieve the result resDX which has the type float32 []:
// Create DX9 target and compute result
use dx9Target = new DX9Target()
let resDX = dx9Target.ToArray1D(expr (kernelSize-1))
printfn "DX9 --> \r\n%A" resDX
A target only needs to be created once. The first time a target is created for DX9 there is a delay while the system is initialized. For benchmarking it is a good idea to perform a dummy computation first to “warm upâ€� the system.
The previous example convolved a one dimensional (1D) matrix. In this section we show how we can convolve a 2D matrix by applying the convolution independently to each line. This computation is illustrated in the diagram below for the following array of arrays:
[|[|7; 2; 5; 9; 3; 8; 6; 4 |];
[|2; 8; 7; 4; 8; 9; 3; 5 |]|]
An F# version of a 1D convolution of 2D input data is shown below which illustrates convolution in the X and Y directions (independently).
open System
open System
open Microsoft.ParallelArrays
[<EntryPoint>]
let main(args) =
// Declare an input data array
let inputData
= Array2D.map float32 (array2D [ [ 7; 2; 5; 9; 3; 8; 6; 4 ];
[ 2; 8; 7; 4; 8; 9; 3; 5 ] ])
// Declare filter kernel for the convolution
let kernel : = Array.map float32 [| 2; 5; 7; 4; 3 |] ;
let kernelSize = kernel.Length
// Create an Accelerator float parallel array for the F# input array
use inputArray = new FloatParallelArray(inputData)
// Build the expression to convolve in the Y direction
let rec exprY i = let e = kernel.[i] *
ParallelArrays.Shift(inputArray, [| 0; -i |])
if i = 0 then
e
else
e + exprY (i-1)
// Create DX9 target and compute result
use dx9Target = new DX9Target()
let resDXY = dx9Target.ToArray2D(exprY (kernelSize-1))
printfn "DX9 Y-dir --> \r\n%A" resDXY
// Build the expression to convolve in the X direction
let rec exprX i = let e = kernel.[i] *
ParallelArrays.Shift(inputArray, [| -i; 0 |])
if i = 0 then
e
else
e + exprX (i-1)
let resDXY = dx9Target.ToArray2D(exprX (kernelSize-1))
printfn "DX9 X-dir --> \r\n%A" resDXY
0
When run, this code computes the correct values:
$ convolver_fs_1d_of_2d_input.exe
DX9 Y-dir -->
[[147.0f; 137.0f; 118.0f; 106.0f; 115.0f; 120.0f; 124.0f; 133.0f]
[42.0f; 54.0f; 82.0f; 113.0f; 123.0f; 138.0f; 144.0f; 132.0f]]
DX9 X-dir -->
[[147.0f; 42.0f; 105.0f; 189.0f; 63.0f; 168.0f; 126.0f; 84.0f]
[137.0f; 54.0f; 109.0f; 179.0f; 73.0f; 170.0f; 120.0f; 86.0f]]
Although this code performs multiplication, shifting and adding of arrays as we saw before in this case we use a different overloaded functions that work over two dimensional arrays and the shift operation uses a two element array to specify how much to shift by in each direction.
val ParallelArrays.Shift : FloatParallelArray -> int [] -> FloatParallelArray
We can make a two dimensional convolver by first convolving in the x-direction and then convolving in the y-direction. Or we can perform a convolution in the y-direction and then in the x-direction. To convolve a 2D matrix we need to use a version of the shift operator which takes two arguments which describe how much to shift by in each dimension. Shifting just in the x-direction is illustrated in the diagram below.
A function which shifts a 2D array just in the x-direction could be written as:
let rec convolveXDir (kernel : float32 []) i (a : FloatParallelArray)
= let e = kernel.[i] * ParallelArrays.Shift(a, [| -i; 0 |])
if i = 0 then
e
else
e + convolveXDir kernel (i-1) a
This function captures the shifting right along the rows nature of the x-direction convolution by specifying a shift of i elements along the rows for the i-th iteration (but it never shifts down columns hence the value of 0 in the second element of the array literal).
Shifting in the y-direction is illustrated in the diagram below.
A function which shifts a 2D array just in the y-direction could be written as:
let rec convolveYDir (kernel : float32 []) i (a : FloatParallelArray)
= let e = kernel.[i] * ParallelArrays.Shift(a, [| 0; -i |])
if i = 0 then
e
else
e + convolveYDir kernel (i-1) a
This function captures the shifting down along the columns of the y-direction convolution by specifying a shift of i elements along the columns for the i-th iteration (but it never shifts along rows hence the value of 0 in the first element of the array literal).
Rather than define two separate functions for convolving in the X and Y directions we can define just one function and pass a higher order function which allows us to abstract the direction of convolution.
// Declare a function to convolve in the X or Y direction
let rec convolve (shifts : int -> int []) (kernel : float32 []) i (a : FloatParallelArray)
= let e = kernel.[i] * ParallelArrays.Shift(a, shifts i)
if i = 0 then
e
else
e + convolve shifts kernel (i-1) a
// Declare a 2D convolver
let convolveXY kernel input
= // First convolve in the X direction and then in the Y direction
let convolveX = convolve (fun i -> [| -i; 0 |]) kernel (kernel.Length - 1) input
let convolveY = convolve (fun i -> [| 0; -i |]) kernel (kernel.Length - 1) convolveX
convolveY
Note that the convolution function takes a higher order parameter which specifies the shift direction. To convolve in the x-direction we provide a function which is given the degree to shift by i and return the (dx, dy) shift to be applied to the data parallel array i.e. (-i, 0). To shift in the y-direction we provide another function which is given the degree to shift by i and return the (dx, dy) shift to be applied to the data parallel array i.e. (0, -i). We use lambda expressions to defines these functions anonymously (in-line) as arguments to the convolve function.
To run the 2D F# convolver please follow these steps.
· Install Accelerator V2.
· Create a new F# console project and paste in the 2D convolver code at the start of this blog.
· If you are not running a 64-bit operating system please remove the code for using the x64 multi-core target i.e. delete the lines:
// Create a X64 multi-core target and use it to convolve the test input
use x64MCTarget = new X64MulticoreTarget()
let convolveMC = x64MCTarget.ToArray2D (convolveXY testKernel testArray)
printfn "MC: -> \r\n%A" convolveMC
· Add a reference to System.Drawing and the managed Microsoft.Accelerator.dll (under the appropriate directory for your target e.g. C:\Program Files (x86)\Microsoft\Accelerator v2\bin\Managed\Release\Microsoft.Accelerator.dll
· Build under Visual Studio.
· Make sure that you have the right Accelerator.dll in your path for your platform and target e.g. C:\Program Files (x86)\Microsoft\Accelerator v2\bin\x64\Release\Accelerator.dll or make sure to have a copy of this file in your build directory.
· Run the generated EXE from the build directory e.g. bin/Release
If you want to use Accelerator code from inside F# Interactive you will need to reference the Accelerator library e.g.:
#r @"C:\Program Files (x86)\Microsoft\Accelerator v2\bin\Managed\Release\Microsoft.Accelerator.dll";;
The Accelerator system encourages you to express data-parallel algorithms in terms of whole array operations which leads to efficient implementations for various back ends (targets). For example, the discipline of using only whole array operations allows me to make efficient address generator circuits for an experimental FPGA target that I am working on.
Accelerator is quite well suited for writing stencil-style data parallel programs. The expression orientated nature of Accelerator computations make them a nice fit for a functional language like F#. In effect the Accelerator system manifests itself as a domain specific language in F#, C# and C++ (as well as other .NET languages).
The F# code in this blog was written with the participation of Lubomir Litchev and James Margetson. Thank you Lubo and James! I aslo recommend this article on using Accelerator from F#: https://tomasp.net/blog/accelerator-intro.aspx.
The Accelerator system is still a research incubation project and the preview release is designed to solicit feedback. You can email msraccel@microsoft.com or use the Microsoft Connect Feedback Form. Thank you!
Satnam Singh
https://research.microsoft.com/~satnams
Comments
Anonymous
December 15, 2009
Thanks Satnam. If you read this excellant blog, you'll probably also enjoy " ...Can non-numerical application developers take advantage from the new LRBni instructions?, by Daniele Paolo Scarpazza — a member of the Multicore Computing Department at the IBM T. J. Watson Research Center. He is the author of articles and scholarly papers on parallel algorithms and performance optimization on emerging multicore architectures http://i.cmpnet.com/ddj/digest/2009/DDD_1209.pdfAnonymous
December 16, 2009
FYI: Although this feed is visible in Google Reader, the post is not. I've not tried other readers, so I don't know whether it affects them as well or not.Anonymous
December 16, 2009
The comment has been removedAnonymous
December 17, 2009
Hello Jurgen. You should be able to omit the FLoatParallelArray type declaration and write: let rec expr (i : int) = let e = ParallelArrays.Shift(inputArray, [| -i |]) * kernel.[i] if i = 0 then e else e + expr (i-1) In this case you need to give the type of i because there are several possible overloads for ParallelArrays.Shift(inputArray, [| -i |]) and the algorithm used for type inference can’t pick a specific one automatically.Anonymous
December 21, 2009
The comment has been removedAnonymous
December 21, 2009
Alexander, I am very sorry for the problems that you are encoutering and I've had a similar report from one other person. I checked again and the code at the top of this post works for me using Visual Studio 2010 Beta 2 and Visual Studio 2008 with F# 1.9.7.8. Please can you email me at satnams@microsoft.com to let me know exactly what version of Visual Studio and F# you are using and I shall do my best to try and get to the bottom of this issue. Once again, profuse apologies for the problems you are encountering. Cheers, SatnamAnonymous
December 21, 2009
Alexnader, I think you may have missed out the final 0? The main function needs to return an int value. That would expalin the error message. Cheers, SatnamAnonymous
September 28, 2010
I can't add a reference to Accelerator.dll in VS 2010 F# project. Any idea why?Anonymous
February 25, 2011
You need the managed assembly - Accelerator v2/bin/Managed VisualStudioaccelerator-introCalculatingPIMicrosoft.Accelerator.dllAnonymous
December 29, 2012
It seems that Accelerator v2 is superior to Task Programming Library (msdn.microsoft.com/.../dd460717.aspx). Do you agree? Does TPL have any advantages over Accelerator v2? It seems that Accelerator v2 should eventually team up or somehow make its way into standard .NET somehow so that vectorization and making use of SIMD/SSE and multiple GPUs..Anonymous
December 19, 2013
The comment has been removed