Un peu de théorie pour l’apprentissage supervisé – 1ère partie
De façon à rentrer de plein pied dans le monde du Machine Learning, nous souhaitons partager une compréhension commune des principes de l’apprentissage automatique, et expliquer au travers d’une série courte de billet ce qu’est l’apprentissage supervisé et non-supervisé avec des applications ainsi que les moyens d’évaluer un modèle en apprentissage automatique.
Ce billet est pour l’essentiel une republication sur ce blog du billet éponyme déjà publié sur le blog Big Data France .
Je vous souhaite une bonne lecture de ce billet
--Philippe
_________________________________________________________________________________________
Nous poursuivons notre exploration de l’apprentissage automatique (Machine Learning) ; la disponibilité de la préversion publique d’Azure Machine Learning (Azure ML) depuis le 14 juillet dernier va nous donner à n’en point douter l’occasion d’illustrer par la pratique tout cela très rapidement.
Pour résumer les épisodes ou plutôt les billets précédents, nous avons pu échanger sur les principes du Machine Learning, et plus particulièrement détailler le fonctionnement de l’apprentissage non-supervisé, fonctionnement qui a été illustré avec une application concrète.
Dans la suite logique des choses, nous allons donc nous intéresser aux principes de fonctionnement des méthodes d’apprentissage supervisé.
On distingue deux grandes familles de tâches réalisables en apprentissage supervisé, à savoir :
- La classification
- La régression
A toutes fins utiles, rappelons que nous parlons de classification lorsque le label à prédire est discret, et nous parlons de régression lorsque le label à prédire est continu.
Dans cette première partie du billet, nous allons nous intéresser aux principales méthodes de classification : arbres de décision et SVM (Support Vecteur Machine). Nous nous intéressons dans la seconde partie de ce billet à la régression.
Pour ce parcours, nous en profiterons pour introduire quelques notions en statistiques et illustrerons le fonctionnement de ces algorithmes en utilisant le jeu de données iris.
Jeu de données iris
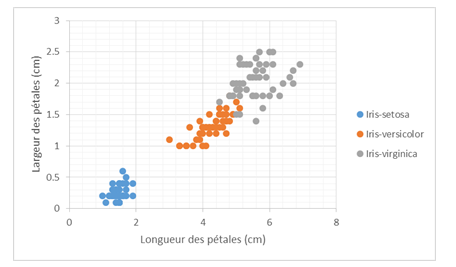
Il existe de nombreux jeux de données publics sur le Machine Learning Repository. L’un des jeux de données les plus populaires est le jeu de données iris téléchargeable ici. Il s’agit d’un historique recensant les dimensions (longueur des sépales, largeur des sépales, longueur des pétales, et largeur des pétales) de 150 iris et l’espèce associée à chaque iris (prédiction) :
A partir des dimensions des iris, nous allons essayer d’entraîner un classifieur qui prédit l’espèce associée : Iris-setosa, Iris-versicolor ou Iris-virginica.
Cette illustration entre dans le cas de la classification car nous disposons d’un historique de données labélisées, et le nombre de valeurs prises par le label à prédire est fini.
Vocabulaire et notations en statistiques
Variable aléatoire
Dans le jargon mathématique, on parle souvent de variable aléatoire notée X. La valeur d’une variable aléatoire change en fonction de ce que l’on appelle une réalisation ![clip_image002[4] clip_image002[4]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/66/54/metablogapi/6866.clip_image0024_thumb_72C58F09.png) .
.
Dans notre illustration, nos 4 caractéristiques et notre label à prédire constituent 5 variables aléatoires discrètes. Les réalisations sont les Iris eux-mêmes.
Plusieurs indicateurs permettent de décrire une variable aléatoire X , en l’occurrence :
- L’espérance représente la moyenne selon les réalisations (plus de détails ici) :
- L’écart type représente la dispersion des données (plus de détails ici) :
Corrélation
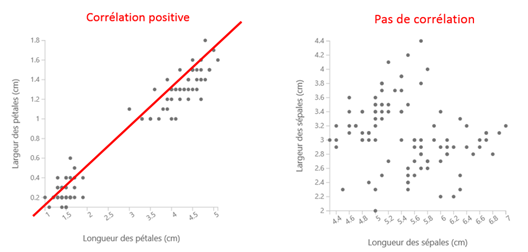
La corrélation est une mesure de la dépendance entre 2 variables aléatoires (plus de détail ici). Par exemple, on remarque que chaque fois que la longueur des pétales est grande alors la largeur des pétales est grande. On dit ainsi qu’il y a une corrélation positive entre la longueur et la largeur des pétales. Par contre, il n’y a pas de corrélation entre la longueur des sépales et la largeur des sépales, on dit alors que ce sont deux variables indépendantes.
Il est important de comprendre que la corrélation n’est qu’une mesure de la dépendance entre 2 variables ; cela n’implique pas nécessairement qu’il existe une causalité entre ces 2 variables (bien que ce soit souvent le cas). Par exemple, les personnes qui boivent un verre de vin par jour ont une durée de vie plus élevée que la moyenne. Toutefois, on ne peut pas conclure que boire un verre de vin par jour augmente la durée de vie ! Dommage… ;-)
Indicateurs de corrélation
On distingue plusieurs indicateurs mesurant la corrélation entre deux variables aléatoires X et Y. Pour n’en citer que deux, on retrouve :
- Le coefficient de corrélation linéaire de Bravais-Pearson :
- L’information mutuelle (plus de détail ici) :
Premier algorithme : arbres de décision
Les algorithmes à base d’arbres de décision sont très populaires. A partir d’un historique, ils établissent des règles qui permettent de déterminer le label à prédire en fonction des caractéristiques. Ces règles se représentent intuitivement sous forme d’arbre. Appliquer l’un de ces algorithmes sur nos données donnerait un résultat de la forme :
« Si la largeur des pétales est inférieure à 3.5, alors l’Iris est de type Iris-setosa, sinon l’iris est de type Iris-virginica »
Les arbres de décision ont l’avantage d’être aisément interprétables par un humain et très rapidement applicables par une machine. En revanche, ils posent parfois des problèmes de sur-apprentissage et sont peu robustes : un faible changement dans les données d’apprentissage peut modifier de manière significative le résultat.
Application « à la main » sur le jeu de données Iris
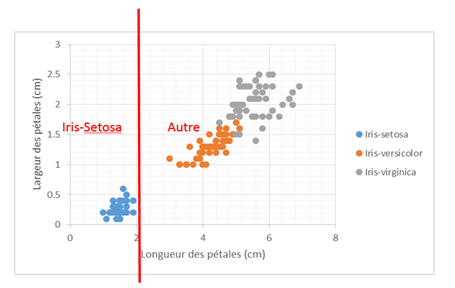
Si l’on restreint les attributs à la longueur et la largeur des pétales, on peut visualiser les données de la manière suivante :
Posons la règle suivante :
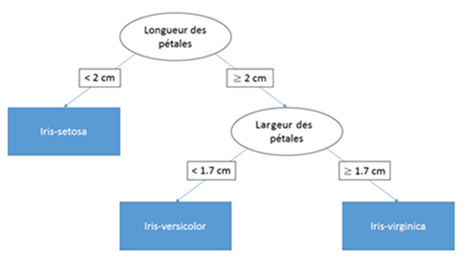
« Si la longueur des pétales est inférieure à 2, alors l’iris est de type Iris-setosa »
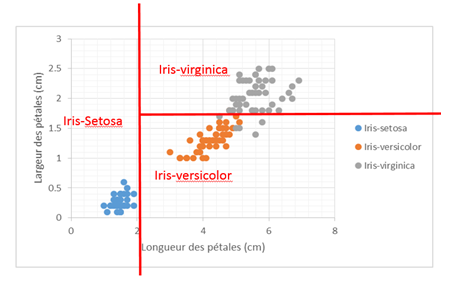
Ensuite, il ne reste que l’attribut largeur des pétales à traiter.
La règle est la suivante :
« Si la largeur des pétales est supérieure à 1.7, l’iris est de type Iris-virginica, sinon il est de type Iris-versicolor »
L’arbre peut donc être visualisé sous la forme suivante :
Algorithme général
L’algorithme se déroule de la manière suivante :
- Calculer la quantité d’information de chaque attribut, c’est-à-dire, la corrélation de chaque attribut au résultat
- Pour l’attribut qui apporte le plus d’information, choisir la meilleure règle « Si A alors B » :
- Déterminer A
- Pour un attribut à valeurs discrètes, les valeurs de A pour chaque règle sont les valeurs prises par l’attribut
- Pour un attribut à valeurs continues, A est le seuil qui classifie « au mieux » tous les éléments. En particulier, si tous les attributs sont continus, on obtient un arbre binaire
- Déterminer B
- Si la classe à prédire est la même pour toutes les réalisations lorsqu’on applique la règle « Si A », alors B est la classe à prédire
- Sinon, B est une nouvelle règle déterminée en réappliquant cet algorithme sur les éléments restants
- Déterminer A
Algorithmes avancés utilisant les arbres de décision
Boosting
Le Boosting est une méthode qui consiste à combiner plusieurs classifieurs afin d’en obtenir un plus performant. Ainsi, au lieu d’entraîner un seul classifieur complexe, on entraîne des classifieurs extrêmement simples (comme des arbres de décision) et la prédiction est obtenue en pondérant les réponses de tous les classifieurs.
Une des méthodes de Boosting les plus utilisées est l’AdaBoost.
Bagging
Le Bagging (ou bootstrap aggregating) est une variante de Boosting. Elle consiste à entraîner plusieurs classifieurs sur des sous-ensembles constitués de 63% des données. Le classifieur global renvoie la moyenne des réponses renvoyées par chaque sous-classifieur.
L’algorithme le plus utilisé utilisant ce principe sur les arbres de décision est appelé forêt d’arbres décisionnels ou Random Forest.
Deuxième algorithme : Support Vecteur Machine (SVM)
Pour exprimer la corrélation entre les attributs et le résultat, les arbres de décision utilisent des règles, les SVMs s’appuient sur la notion de distance entre les données expliquée dans un billet précédent. Ces algorithmes sont très performants mais nécessitent beaucoup de temps de calcul.
Appliquer un algorithme de SVM consiste à trouver la courbe qui « sépare au mieux » les données, c’est-à-dire, de telle sorte que tous les éléments au-dessous de cette courbe appartiennent à la classe 1, tous les autres à la classe 2.
Toutefois, une infinité de courbes séparent les données. Il s’agit de trouver la meilleure. Pour cela, on utilise le critère de marge maximale.
SVM linéaire – cas séparable
Reprenons notre jeu de données iris simplifié. On recherche la droite qui sépare le mieux les Iris-setosa et les Iris-versicolor :
Pour cela, on définit la marge comme la plus petite distance entre les points de chaque classe et le séparateur. Il est alors possible de choisir le meilleur séparateur comme étant celui maximisant la marge :
Maximiser la marge permet d’obtenir un meilleur classifieur dans la mesure il faut rester conscient que les données d’apprentissage ne sont pas exhaustives.
Introduction aux méthodes à noyaux – cas général
Dans le cas où les données sont non-séparables - il n’existe pas de droite pour séparer exactement les données -, on peut faire appel aux méthodes à noyaux.
Le principe est d’appliquer une transformation judicieuse sur les données, en général non-linéaire, afin de rendre les données séparables. Il suffit ensuite d’appliquer l’algorithme de SVM linéaire abordé ci-avant, puis d’appliquer la transformation inverse au séparateur (on dit aussi projeter le séparateur).
Lorsque la transformation aussi appelée noyau augmente la dimension des données, on parle de Kernel trick ou astuce du noyau. Dans ce cas, il est possible de trouver un "hyperplan" (généralisation de la droite) qui sépare exactement les données. Cette astuce ouvre vers des sujets vastes comme la malédiction de la dimensionnalité.
Sur notre jeu de données, cela donne :
L’astuce du noyau s’avère dans la pratique très puissante et peut être combinée à de nombreuses méthodes d’apprentissage supervisé (ou non-supervisé) afin d’améliorer les performances de ceux-ci, la difficulté étant de trouver un noyau judicieux…
Algorithme général
L’algorithme complet incluant l’astuce du noyau est le suivant :
- Appliquer une fonction noyau judicieuse afin de transformer les données
- Trouver le classifieur linéaire qui maximise la marge à l’aide d’une méthode d’optimisation
- Projeter le classifieur
Nous espérons vous avoir éclairé sur le fonctionnement des arbres de décision et des SVMs et d’une façon plus générale sur la classification. De nombreuses ressources sont disponibles sur Internet, n’hésitez pas à les consulter si vous souhaitez creuser le sujet.
Les questions et les propositions d’amélioration sont toujours les bienvenues en commentaires :)
La suite de ce parcours sur l’apprentissage supervisé va nous amener à aborder les notions relatives à la régression dans la seconde partie de ce billet.








![clip_image002[5] clip_image002[5]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/66/54/metablogapi/0601.clip_image0025_thumb_440BE835.jpg)