Соединение точек в контур - обратная задача
Имеется готовый LineString, из которого требуется получить таблицу точек - см. Скрипт 1 предыдущего поста. Для закрепления пройденного сделаем это тремя способами. Первый - самый простой: цикл по все точкам ломаной. Второй - получить строку координат точек с помощью GML. Третий - получить строку координат с помощью бинарного представления.
Первый способ.
declare @l geometry = geometry::STGeomFromText('LINESTRING(0 0, 1 1, 1 -1, -1 -1, -1 1)', 0)
declare @t table (id int identity, p geometry)
declare @i int = 1
while (@i <= @l.STNumPoints()) begin
insert @t (p) values (@l.STPointN(@i))
set @i += 1
end
select id, p.ToString() from @t
Рис.1
Второй способ.
declare @l geometry = geometry::STGeomFromText('LINESTRING(0 0, 1 1, 1 -1, -1 -1, -1 1)', 0)
declare @t table (id int identity, XY float)
declare @s varchar(max) = @l.AsGml().value('declare default element namespace "http://www.opengis.net/gml";
(LineString/posList)[1]', 'varchar(max)')
declare @i int = 0, @j int
while (@i < len(@s)) begin
set @j = charindex(' ', @s, @i + 1)
if @j = 0 set @j = len(@s)
insert @t(XY) values (cast(substring(@s, @i + 1, @j - @i -1) as float))
set @i = @j
end
select id1, X, Y from (select id, (id + 1) / 2 id1, XY X, lead(XY, 1) over (order by id) Y from @t) t where id % 2 = 1
Рис.2
Запрос, вытаскивающий из GML строку с координатами вершин, взят из Рис.7 предыдущего поста. Как сделать из координат точку, объяснять не надо. Вместо этого давайте обратим внимание на интересную особенность поведения функции LEAD(), которую мы не отметили в посте Нарастающий итог - обратная задача. Если написать просто
select (id + 1) / 2 id, XY X, lead(XY, 1) over (order by id) Y from @t where id % 2 = 1
-------------------------------------------------------------------------------------
id X Y
1 0 1
2 1 1
3 1 -1
4 -1 -1
5 -1 NULL
Скрипт 1
функция LEAD, как мы видим, работает с учетом условия WHERE, т.е. lead(…, 1) - это результат не из следующей по порядку записи, а из следующей записи, удовлетворяющей WHERE. Чтобы получить значения LEAD из записей, не подпадающих под условие фильтрации, приходится делать двухходовку с использованием СТЕ или подзапроса (Рис.2).
Способ третий.
Через бинарное представление геопространственных величин. Здесь есть пара нюансов. Во-первых, в T-SQL не существует прямой конвертации из varbinary в real/float. Чтобы ее осуществить, надо слегка распарсить бинарный формат представления float. Например, воспользоваться функцией fnBinaryFloat2Float. Во-вторых, это все равно будет недостаточно, т.к. бинарный формат float в SQL Server не вполне совпадает со стандартом IEEE-754. Существует простой, как валенок, способ превращения стандартной бинарной величины в вещественное число SQL Server, который гарантированно будет работать, пока в SQL Server поддерживаются геопространственные типы. Нужно создать точку с такой абсциссой и вернуть ее STX.
if OBJECT_ID('dbo.fnBinaryToDouble', 'FN') is not null drop function dbo.fnBinaryToDouble
go
create function dbo.fnBinaryToDouble(@b as binary(8)) returns float as begin
return geometry::STPointFromWKB(0x01 + 0x01000000 + @b + 0x0000000000000000, 0).STX
end
go
select dbo.fnBinaryToDouble(0x000000000000F03F)
Рис.3
Теперь аналогично Рис.2 можно пройтись циклом по строке @s, в этот раз бинарной. Кол-во @n точек в ломаной получается в соответствии со Скриптом 6 поста Превращение последовательности точек в геометрическую фигуру. Там же после Скрипта 10 объясняется, почему требуется reverse(). Далее в цикле пробегаемся по каждой из n пар координат. Чтобы получить 1-ю координату, надо пропустить 1-байтовый byteOrder, 4-байтный wkbType и 4-байтное же кол-во вершин (@n), т.е. отступить на 9 байт, начав с 10-го. Координата занимает 8 байт, значит, каждая следующая координата будет находиться +8 от предыдущей. Полученную таким образом последовательность байт превращаем во float при помощи функции fnBinaryToDouble (Рис.3). Если это нечетная координата, значит, это абсцисса; в таблице начинаем новую запись. Если четная - это ордината для предыдущей записи. Собственно, вот:
declare @l geometry = geometry::STGeomFromText('LINESTRING(0 0, 1 1, 1 -1, -1 -1, -1 1)', 0)
declare @t table (id int identity, X float, Y float)
declare @s varbinary(max) = @l.STAsBinary()
declare @n int = cast(reverse(substring(@s, 6, 4)) as binary(4)), @i int = 1
declare @XY float
while (@i <= @n * 2) begin
set @XY = dbo.fnBinaryToDouble(substring(@s, 1 + 4 + 4 + 1 + (@i - 1) * 8, 8))
if @i % 2 = 1
insert @t (X) values (@XY)
else
update @t set Y = @XY where id = @i / 2
set @i += 1
end
select * from @t
Рис.4
Как быть, если вместо ломаной фигурирует многоугольник, все вершины которого аналогично требуется переписать в таблицу? Напрашивается получить его границу в виде LineString и свести задачу к предыдущей:
declare @l geometry = geometry::STGeomFromText('POLYGON((0 0, 1 1, 1 -1, -1 -1, -1 1, 0 0))', 0)
select @l.STBoundary().ToString()
-------------------------------------------------------------------------------------
LINESTRING (-1 -1, 1 -1, 1 1, 0 0, -1 1, -1 -1)
Скрипт 2
Однако метод STBoundary() в чистом виде не подходит. Мы помним, что бывают многоугольники с дырками, чья граница состоит из внешнего контура и контуров дырок:
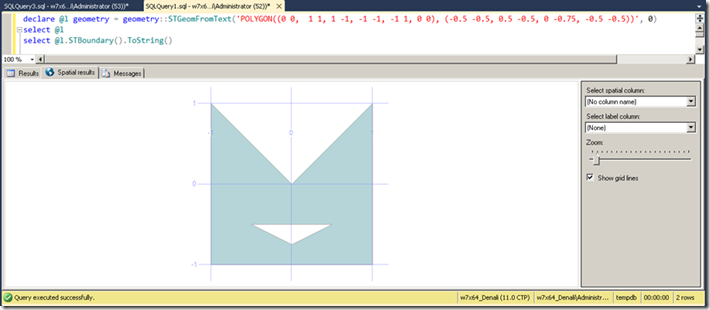
declare @l geometry = geometry::STGeomFromText('POLYGON((0 0, 1 1, 1 -1, -1 -1, -1 1, 0 0), (-0.5 -0.5, 0.5 -0.5, 0 -0.75, -0.5 -0.5))', 0)
select @l.STBoundary().ToString()
-----------------------------------------------------------------------------------------------
MULTILINESTRING ((0 -0.75, -0.5 -0.5, 0.5 -0.5, 0 -0.75), (-1 -1, 1 -1, 1 1, 0 0, -1 1, -1 -1))
Рис.5
Если в этом случае не интересует, к какому контуру относятся точки, можно организовать цикл по границам:
declare @l geometry = geometry::STGeomFromText('POLYGON((0 0, 1 1, 1 -1, -1 -1, -1 1, 0 0), (-0.5 -0.5, 0.5 -0.5, 0 -0.75, -0.5 -0.5))', 0)
declare @i int = 1, @boundary geometry = @l.STBoundary()
while @i <= @boundary.STNumGeometries() begin
select @boundary.STGeometryN(@i).ToString()
set @i += 1
end
-------------------------------------------------------------------------------------
LINESTRING (0 -0.75, -0.5 -0.5, 0.5 -0.5, 0 -0.75)
LINESTRING (-1 -1, 1 -1, 1 1, 0 0, -1 1, -1 -1)
Скрипт 3
Обратите внимание, что STGeometryN(1) совершенно необязательно означает внешнюю границу. Если нужно получить только точки с внешнего контура, следует использовать метод STExteriorRing():
declare @l geometry = geometry::STGeomFromText('POLYGON((0 0, 1 1, 1 -1, -1 -1, -1 1, 0 0), (-0.5 -0.5, 0.5 -0.5, 0 -0.75, -0.5 -0.5))', 0)
select @l.STExteriorRing().ToString()
-------------------------------------------------------------------------------------
LINESTRING (0 0, 1 1, 1 -1, -1 -1, -1 1, 0 0)
Скрипт 4
а для внутренних контуров, соответственно, STInteriorRingN():
declare @l geometry = geometry::STGeomFromText('POLYGON((0 0, 1 1, 1 -1, -1 -1, -1 1, 0 0), (-0.5 -0.5, 0.5 -0.5, 0 -0.75, -0.5 -0.5))', 0)
declare @i int = 1
while @i <= @l.STBoundary().STNumGeometries() - 1 begin
select @l.STInteriorRingN(@i).ToString()
set @i += 1
end
-------------------------------------------------------------------------------------
LINESTRING (-0.5 -0.5, 0.5 -0.5, 0 -0.75, -0.5 -0.5)
Скрипт 5
Алексей Шуленин