WCS Transformations-Erstellungsalgorithmen

Erstellung von Transformationen

 

Sequenzielle Transformationsausführung

 

Erstellung optimierter Transformationen

 

ICCProfileFromWCSProfile

 

schwarze Erhaltung und schwarze Generation

 

Gamut- überprüfen

Erstellung von Transformationen

Um die Funktionsweise von Farbtransformationen ordnungsgemäß zu erläutern, ist es hilfreich, den vollständigen Verarbeitungspfad sowohl über ICM 2.0 als auch über die Internen der CTE zu erläutern. Die ICM 2.0-CreateColorTransformW--Funktion erstellt eine Farbtransformation, die Anwendungen zum Ausführen der Farbverwaltung verwenden können. Diese Funktion erstellt einen Farbkontext aus den LOGCOLORSPACE-- und Intent-Eingaben. Die Absichten werden dem geplanten ICC-Gamutzuordnungsalgorithmus zugeordnet, der korreliert. Anschließend ruft die Funktion ICM 2.0 CreateMultiProfileTransform- für eine konsistente Farbverarbeitung auf. Die CreateColorTransform--Funktion kopiert in der Regel Daten in die interne optimierte Transformationsstruktur.

Die ICM 2.0 CreateMultiProfileTransform-Funktion akzeptiert ein Array von Profilen und ein Array von Absichten oder ein einzelnes Geräteverknüpfungsprofil und erstellt eine Farbtransformation, mit der Anwendungen Farbzuordnungen durchführen können. Es verarbeitet diese Eingabeprofile und Absichten zum Erstellen von Gerätemodellen, Farbdarstellungsmodellen, Beschreibungen von Gamutgrenzen und Gamut-Zuordnungsmodellen. Gehen Sie wie folgt vor:

• Gerätemodelle werden direkt aus DM-Profilen initialisiert. Es gibt ein Gerätemodell, das für jedes Profil im Aufruf von CreateMultiProfileTransformerstellt wird.
• Farbdarstellungsmodelle werden direkt aus CAM-Profilen initialisiert. Es gibt ein CAM-Profil für jedes Profil im Aufruf von CreateMultiProfileTransform. Das gleiche CAM-Profil kann jedoch für mehrere Profile angegeben werden.
• Beschreibungen von Gamut-Begrenzungen werden aus einem Gerätemodellobjekt und einem CAM-Objekt initialisiert. Für jedes Profil im Aufruf von CreateMultiProfileTransform-gibt es eine Allgemeine Begrenzungsbeschreibung.
• Gamut-Zuordnungsmodelle werden aus zwei Gamut-Begrenzungen und einer Absicht initialisiert. Sie müssen ein Gamut-Zuordnungsmodell zwischen jedem Gerätemodellpaar erstellen, das aus dem Aufruf von CreateMultiProfileTransformerstellt wurde. Beachten Sie, dass Dies bedeutet, dass Sie ein weniger Gamut-Kartenmodell als das Gerätemodell verwenden. Da die Anzahl der Absichten mit der Anzahl der Gerätemodelle übereinstimmt, gibt es auch eine weitere Absicht als erforderlich. Die erste Absicht in der Liste wird übersprungen. Sie werden durch die Liste der Gerätemodelle und -absichten geführt, indem Sie Gamut-Zuordnungsmodelle erstellen. Rufen Sie die ersten und zweiten Gerätemodelle und die zweite Absicht auf, und initialisieren Sie dann das erste Gamut-Zuordnungsmodell. Nehmen Sie die zweiten und dritten Gerätemodelle und die dritte Absicht auf, und initialisieren Sie dann das zweite Gamut-Zuordnungsmodell. Fahren Sie auf diese Weise fort, bis Sie alle Gamut-Zuordnungsmodelle erstellt haben.

Wenn die Profile ordnungsgemäß verarbeitet wurden und alle Zwischenobjekte erstellt und initialisiert wurden, können Sie die CITE-Transformation mit dem folgenden Aufruf erstellen. Die pDestCAM und pDestDM- sind diejenigen, die dem letzten Profil im Aufruf von CreateMultiProfileTransformzugeordnet sind.

HRESULT CreateCITEColorTransform(
 __inout     IDeviceModel          *pSourceDM,
 __inout     IColorAppearanceModel *pSourceCAM,
 __in        GamutMapArray         *pGamutMapArray,
 __inout     IColorAppearanceModel *pDestCAM,
 __inout     IDeviceModel          *pDestDM,
             EColorTransformMode    eTransformMode,
 __deref_out IColorTransform      **ppCTS
 );

Unterstützung für Plug-Ins

Ein Problem beim Einrichten der Transformationsliste besteht darin, zu überprüfen, ob ein erforderliches Plug-In verfügbar ist. Der folgende Modellwechsel stellt diese Richtlinie bereit, um dieses Verhalten zu steuern. Die Verwaltung dieser Transformationsliste ist eine Methode in der internen optimierten Transformationsstruktur, aber jede Modellmethode stellt den Zeiger auf sich selbst und einen eigenen Satz von Parameterwerten bereit.

Der Modus muss einer der folgenden Sein.

• TfmRobust: Wenn ein Messprofil ein bevorzugtes Plug-In angibt und das Plug-In nicht verfügbar ist, verwendet das neue CTE-System das Basis-Plug-In. Wenn kein Plug-In verfügbar ist, meldet die Transformation einen Fehler.
• TfmStrict: Wenn der ColorContext ein bevorzugtes Plug-In angibt, muss das Plug-In verfügbar sein. Wenn kein bevorzugtes Plug-In gefunden wird, wird das Basis-Plug-In verwendet. Wenn kein Plug-In verfügbar ist, meldet die Transformation einen Fehler.
• TfmBaseline: Nur Basisplan-Plug-Ins können in AddMeasurementStep verwendet werden. Wenn der ColorContext ein bevorzugtes Plug-In angibt, wird das Plug-In ignoriert. Wenn das Basis-Plug-In nicht verfügbar ist, meldet die Transformation einen Fehler.

Transformieren der Ausführung

Die ICM 2.0-API TranslateColors-Funktion übersetzt ein Array von Farben aus der Quelle Farbraum in den Zielfarbraum, wie durch eine Farbtransformation definiert. Diese Funktion überprüft intern ein Array zwischengespeicherter Farben, um die sofortige Übereinstimmung von häufig transformierten Farben zu ermöglichen. Diese Transformation unterstützt 8-Bit-Bytearrays und 32-Bit pro Kanal-Float-Arrays. Alle anderen Formate werden vor der Übergabe an den neuen CTE konvertiert.

Die ICM 2.0-API TranslateBitmapBits--Funktion übersetzt die Farben einer Bitmap mit einem definierten Format, um eine andere Bitmap in einem angeforderten Format zu erzeugen. Diese Funktion überprüft intern ein Array zwischengespeicherter Farben, um die sofortige Übereinstimmung von häufig transformierten Farben zu ermöglichen. Um zu viele Codepfade, Unterstützung und Testkomplexität zu vermeiden, werden nur eine begrenzte Anzahl von Bitmapformaten tatsächlich im Transformations- und Interpolationsmodul unterstützt. Diese Funktion muss die nicht nativen ein- und ausgehenden Bitmapformate in systemeigene unterstützte Formate für die Verarbeitung übersetzen. Diese Transformation unterstützt nur 8-Bit pro KanalByte-Bitmaps und 32-Bit pro Kanal-Float-Bitmaps. Alle anderen Formate werden vor der Übergabe an den neuen CTE konvertiert.

 

Sequenzielle Transformationsausführung

Wenn der dwFlags Parameter den SEQUENTIAL_TRANSFORM Bitsatz aufweist, wenn die ICM-Funktionen CreateColorTransformW oder CreateMultiProfileTransform aufgerufen werden, werden die Transformationsschritte sequenziell ausgeführt. Dies bedeutet, dass der Code jedes Gerätemodells, Farbdarstellungsmodells und Gamut-Zuordnungsmodell separat durch die CreateColorTransform- oder CreateMultiProfileTransform- Aufruf angegeben wird. Dies kann beim Debuggen von Plug-In-Modulen hilfreich sein, ist aber viel langsamer als die Ausführung durch eine optimierte Transformation. Die Ausführung im sequenziellen Modus wird daher für Produktionssoftware nicht empfohlen. Außerdem kann es geringfügige Unterschiede in den Ergebnissen geben, die im sequenziellen Modus und im optimierten Modus erzielt wurden. Dies liegt an Variationen, die beim Verketten der Funktionen eingeführt werden.

Erstellung optimierter Transformationen

Eine optimierte Transformation ist eine mehrdimensionale Nachschlagetabelle. Die Tabelle kann von einem mehrdimensionalen Interpolationsmodul verarbeitet werden, z. B. tetraedrale Interpolation, das die Eingabefarben auf die Transformation anwendet. Im folgenden Abschnitt wird beschrieben, wie die optimierten Nachschlagetabellen erstellt werden. Im Abschnitt danach wird beschrieben, wie sie innerhalb der optimierten Nachschlagetabellen interpoliert werden.

Geringe Nachschlagetabellen

Herkömmliche Drucker verfügen über CMYK-Druckfarben. Um die Gamut zu erweitern, besteht ein Ansatz darin, dem System neue Freihandfarben hinzuzufügen. Die in der Regel hinzugefügten Tinten sind Farben, die CMYK-Tinten schwierigkeiten bei der Wiedergabe haben. Häufige Auswahlmöglichkeiten sind Orange, Grün, Rot, Blau usw. Um die "scheinbare Auflösung" zu erhöhen, können Druckfarben mit unterschiedlichen Farbtons verwendet werden, z. B. helles Zyan, helles Magenta usw. Tatsächlich verfügt das Druckergerät über mehr als vier Kanäle.

Obwohl Drucker Ausgabegeräte sind, führen sie auch die Farbkonvertierung vom Gerätebereich in einen anderen Farbraum aus. Bei einem CMYK-Drucker wäre dies eine Transformation von CMYK zu XYZ oder das "Forward Model" des Druckers. Durch die Kombination des Vorwärtsmodells mit anderen Transformationen ist es möglich, einen CMYK-Druck auf einem anderen Gerät zu emulieren. Beispielsweise würde ein Drucker CMYK auf einem Monitor RGB einen Korrekturmechanismus ermöglichen, der einen Druck dieses CMYK-Druckers auf einem Monitor emuliert. Das gleiche gilt auch für hi-fi Drucker. Eine CMYKOG in RGB-Konvertierung ermöglicht die Korrektur des CMYKOG-Druckers auf einem Monitor.

Der herkömmliche Ansatz zur Implementierung einer solchen Farbkonvertierung ist die Verwendung eines EINHEITLICHEN LUT. In einem ICC-Profil für einen CMYKOG-Drucker mandatiert die ICC-Spezifikation beispielsweise ein A2B1-Tag, das einen EINHEITLICHEN LUT speichert, der ein einheitliches Sampling im CMYKOG Gerätebereich des Vorwärtsmodells darstellt, das von CMYKOG zum ICC-Profilverbindungsraum (CIELAB oder CIEXYZ) geht. Das ICC-Geräteverknüpfungsprofil ermöglicht eine direkte Transformation von CMYKOG-Geräteraum zu jedem Farbraum, einschließlich eines Geräteraums, auch in Form eines LUT, der einheitlich im CMYKOG-Raum gemustert wird. Sampling wird nie mit 256 Ebenen (Bittiefe 8) aufgrund der riesigen LUT durchgeführt, außer bei Monochromgeräten (1 Kanal). Stattdessen wird das Sampling mit niedrigerer Bittiefe verwendet; Einige typische Auswahlmöglichkeiten sind 9 (Bittiefe 3), 17 (Bittiefe 4), 33 (Bittiefe 5). Bei der Anzahl der Ebenen unter 256 in jedem Kanal wird der LUT in Verbindung mit einem Interpolationsalgorithmus verwendet, um das Ergebnis zu erzeugen, wenn eine Ebene zwischen zwei stichprobenierten Ebenen liegt.

Während eine einheitliche LUT konzeptionell einfach zu implementieren ist und interpolation auf einem LUT im Allgemeinen effizient ist, nimmt die LUT-Größe exponentiell mit der Eingabedimension zu. Wenn d tatsächlich die Anzahl der Schritte ist, die im LUT verwendet werden, und n die Anzahl der Kanäle im Quellfarbraum ist, ist die Anzahl der Knoten im LUT 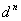. Klar, die Anzahl der Knoten benötigt schnell so viel Speicher im Arbeitsspeicher, dass selbst top-of-the-line Computing-Systeme Schwierigkeiten bei der Behandlung der Nachfrage haben. Für Geräte mit sechs oder acht Kanälen erfordert eine ICC-Implementierung des Geräteprofils einige Schritte im LUT, manchmal sogar bis zu fünf Schritte in der A2B1-Tabelle, um das Profil innerhalb von Megabytes anstelle von Gigabyte beizubehalten. Deutlich erhöht die Verwendung einer kleineren Anzahl von Schritten den Interpolationsfehler, da jetzt weniger Stichproben vorhanden sind. Da die LUT einheitlich sein muss, wird die Genauigkeit über den gesamten Farbraum sogar in den Bereichen des Raums beeinträchtigt, in denen ein erheblicher Farbunterschied durch kleine Änderungen am Gerätewert verursacht werden kann.

Bei Geräten mit mehr als vier Farbstoffen sind bestimmte Unterräume des gesamten Gerätebereichs wichtiger als andere. Im CMYKOG-Raum werden z. B. Cyan- und Grünfarben selten zusammen verwendet, da sich ihre Farbtons weitgehend gegenseitig überlappen. Ebenso überlappen sich gelben und orangefarbenen Tinten weitgehend gegenseitig. Eine einheitliche Reduzierung der Anzahl der Schritte kann als gesamter Qualitätsverlust im gesamten Farbraum betrachtet werden, was Sie sich für die unwahrscheinlichen Freihandkombinationen, aber nicht für die wahrscheinlichen oder wichtigen Kombinationen leisten können.

Während eine einheitlich bemusterte LUT einfach und effizient für die Interpolation ist, stellt sie große Speicheranforderungen fest, da die Dimension zunimmt. In wirklichkeit, während ein Gerät möglicherweise sechs oder acht Kanäle hat, werden sie selten gleichzeitig verwendet. In den meisten Fällen weist die Eingabefarbe in die Farbtransformation nur einige "aktive" Farbmittel auf und befindet sich daher in einem unteren dimensionalen Farbraum. Dies bedeutet auch, dass die Interpolation in diesem unteren dimensionalen Raum effizienter erfolgen kann, da die Interpolation schneller ist, wenn die Dimension niedriger ist.

Daher besteht der Ansatz darin, den gesamten Geräteraum in Unterräume verschiedener Dimensionen zu stratifizieren. Und da niedrigere Dimensionen (diejenigen, die drei oder vier Farbstoffe kombinieren) wichtiger sind, können Sie auch verschiedene Samplingraten anwenden, indem Sie den Raum stratifizieren; das heißt, eine andere Anzahl von Schritten zu den Stücken; Erhöhung der Samplingraten für niedrigere Dimensionen, wodurch sie für höhere Dimensionen reduziert werden.

Um Notationen zu beheben, ist n die Anzahl der Kanäle im Quellfarbraum der Farbtransformation, die Sie beispielen möchten. Sie können auch auf n als Eingabedimension verweisen, und 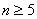, sofern nicht anders angegeben.

Die grundlegenden Bausteine sind LUTs verschiedener Eingabe-Dimensionen und Größen, anstelle einer EINHEITLICHEN LUT mit Eingabedimension n. Um genauer zu sein, ist einLUT ein rechteckiges Gitter, das einem Einheitswürfel auferlegt wird; d. a. alle Gerätekoordinaten werden in den Bereich [0, 1]normalisiert. ist die Eingangsdimension des Luts (beachten Sie, dass nicht gleich nsein muss, obwohl 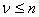ist erforderlich), dann besteht es aus ν-eindimensionalen Sampling-Rastern:

Samp i: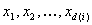

wobei alle x_js im Bereich liegen müssen [0, 1], 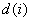ist die Anzahl der Schritte für das i th Channel Sampling, das mindestens 1 sein muss, und 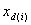muss 1 sein. Auf der anderen Seite zeigt 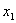muss nicht 0 sein.

Nur die folgenden beiden Sonderfälle von LUT werden definiert.

Geschlossene LUT-: Dies ist eine LUT mit der zusätzlichen Anforderung, dass für jeden Samp*_i*, 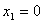und 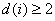. Ein einheitliches geschlossenes LUT ist ein geschlossenes LUT mit demselben 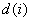für jeden Kanal und die Knoten sind gleichmäßig zwischen 0 und 1 angeordnet.

Open LUT: Dies ist eine LUT mit der zusätzlichen Anforderung, dass für jeden Samp i, 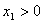. Es ist OK, .

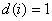Ziel ist es, den Einheitswürfel [0, 1] n in eine Sammlung geschlossener LUTs und offene LUTs zu stratifizieren, sodass die gesamte Sammlung den Einheitswürfel abdeckt. Es ist konzeptionell einfacher, diese "LUT-Schichten" nach ihren Dimensionen zu organisieren, so dass auf oberster Ebene:

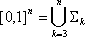
wobei 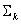ist die "k -dimensional strata collection". Beachten Sie, dass die Strata-Dimension von 3 anstelle von 0 beginnt; Das heißt, Punkte, da die Interpolation von dreifarbigen Kombinationen ohne zu viel Arbeitsspeicherbedarf behandelt werden kann.

Beschreibung der LUT-Schicht

In dieser Implementierung:

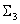1. besteht aus geschlossenen LUTs mit drei Eingaben, eine aus jeder möglichen Kombination von drei Farbstoffen, die aus den n Farbmitteln ausgewählt wurden.

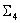2. besteht aus einem geschlossenen LUT für die Kombination CMYK (oder die ersten vier Farbstoffe) zusammen mit 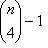öffnen Sie LUTs für alle anderen vierfarbigen Kombinationen. Durch das Aussenden der CMYK-Kombination erkennen Sie an, dass es sich um eine wichtige Kombination handelt.

3. Für 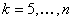, 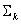besteht aus 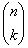geöffnete LUTs, eine für jede mögliche Kombination, k Farbstoffe aus der Summe der n Farbstoffe auszuwählen.

Es bleibt dabei, die Größen der LUTs anzugeben. Der hauptunterschied zwischen offenen und geschlossenen LUTs besteht darin, dass offene LUTs sich nicht überlappen, und geschlossene LUTs können sich an den Begrenzungsflächen überlappen. Die Tatsache, dass das eindimensionale Sampling in einem offenen LUT nicht 0 enthält, bedeutet im Wesentlichen, dass eine offene LUT die Hälfte der Grenzflächen fehlt, daher der Name "offen". Wenn sich zwei LUTs nicht überlappen, können Sie eine andere Anzahl von Schritten oder Knotenspeicherorten in jedem Kanal verwenden. Dasselbe gilt nicht, wenn sich zwei LUTs überlappen. Wenn die Anzahl der Schritte oder Knotenpositionen unterschiedlich ist, erhält in diesem Fall ein Punkt, der im Schnittpunkt der beiden LUTs liegt, einen anderen Interpolationswert, je nachdem, welcher LUT in der Interpolation verwendet wird. Eine einfache Lösung für dieses Problem besteht darin, einheitliche Samplings mit derselben Anzahl von Schritten zu verwenden, wenn zwei LUTs überlappen. Mit anderen Worten,:

Alle geschlossenen LUTs (alle dreifarbigen LUTs und die CMYK LUT in dieser Implementierung) müssen einheitlich sein und dieselbe Anzahl von Schritten aufweisen, die dangegeben werden.

Die folgenden beiden Algorithmen können verwendet werden, um die Anzahl der Schritte d für geschlossene LUTs und die Anzahl der Schritte für offene LUTs zu bestimmen.

Algorithmus Nr. 1

Dieser Algorithmus erfordert keine externe Eingabe.

Alle geschlossenen LUTs sind einheitlich mit d Anzahl der Schritte.

Alle geöffneten LUTs der Dimension k haben die gleiche Anzahl von Schritten 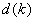in jedem Eingabekanal, und die Knoten sind gleichmäßig verteilt; d. h. für jede .

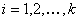Samp i: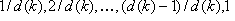

Geben Sie schließlich d und d (k ) in der folgenden Tabelle 1 an. Die drei Modi "Proof", "normal" und "best" sind die ICM 2.0-Qualitätseinstellungen. In dieser Implementierung verfügt der Korrekturmodus über den kleinsten Speicherbedarf, und der beste Modus verfügt über den größten Speicherbedarf.

Um diesen Algorithmus zu implementieren, müssen Sie den folgenden Algorithmus #2 aufrufen. Benutzer können ihre eigenen Samplingspeicherorte mithilfe der Tabellen als Leitfaden angeben.

Algorithmus Nr. 2

Dieser Algorithmus erfordert externe Eingaben in Form einer Liste der "wichtigen" Samplingspeicherorte, ist aber adaptiver und kann potenziell Speicherplatz sparen.

Die erforderliche Eingabe ist ein Array von Gerätewerten, die vom Benutzer bereitgestellt werden. Diese Gerätewerte geben an, welcher Bereich des Gerätefarbraums wichtig ist; d. h., welche Region mehr stichprobeniert werden sollte.

Alle geschlossenen LUTs sind einheitlich mit d Anzahl der Schritte, wie in Algorithmus Nr. 1 beschrieben. Werte für d werden in Tabelle 1 angegeben.

(a) Uniform Closed LUT

	Korrekturmodus	Normalmodus	Optimaler Modus
d	9	17	33

 

(b) Open LUT

Eingabedimension	Korrekturmodus	Normalmodus	Optimaler Modus
4	5	7	9
5	2	3	3
6	2	3	3
7	2	2	2
8 oder mehr	2	2	2

 

Tabelle 1: im Algorithmus verwendeten LUT-Größen

Jede offene LUT kann eine andere Anzahl von Schritten in jedem Eingabekanal aufweisen, und die Samplingspeicherorte müssen nicht gleich groß sein. Bei einer bestimmten offenen LUT-Schicht gibt es eine zugeordnete Farbkombination, z. B. 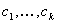, wobei die 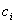sind unterschiedliche ganze Zahlen zwischen 1 und n. Sie sind die Kanalindizes, die den "aktiven" Farbstoffen in dieser Schicht entsprechen.

SCHRITT 1: Filtern Sie das eingegebene Array von Gerätewerten, die nicht in dieser Schicht enthalten sind. Ein Gerätewert 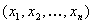ist in der Schicht enthalten, wenn 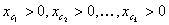und alle anderen Kanäle sind 0. Wenn der gefilterte Satz N- Einträge enthält, lassen Sie

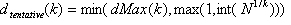
Für jede 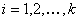, durchlaufen Sie die folgenden Schritte 2-5:

SCHRITT 2: Wenn 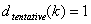, Samp i hat nur 1 Punkt, die 1,0 sein muss. Fahren Sie mit dem nächsten ifort. Fahren Sie andernfalls mit SCHRITT 3 fort.

SCHRITT 3: Sortieren Sie die gefilterten Beispiele in aufsteigender Reihenfolge in der 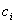Kanal an.

SCHRITT 4: Definieren des Samplingrasters "mit Vorbehalt" mithilfe der Knoten

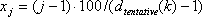
wobei .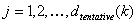

SCHRITT 5: Reguläres Gitter mit Vorbehalt, um sicherzustellen, dass es streng monotonisch ist und auch mit 1,0 endet. Da das Array bereits sortiert ist, sind die Knoten im vorläufigen Raster bereits monotonisch und nicht dekrementiert. Benachbarte Knoten können jedoch identisch sein. Sie können dies beheben, indem Sie bei Bedarf identische Knoten entfernen. Wenn der Endpunkt nach diesem Verfahren kleiner als 1,0 ist, ersetzen Sie ihn durch 1,0.

Beachten Sie, dass SCHRITT 5 der Grund dafür ist, dass die LUT-Schicht möglicherweise eine andere Anzahl von Schritten in jedem Kanal hat. Nach der Normalisierung kann die Anzahl der Schritte in einem Kanal kleiner als .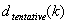

Interpolation

Sie können die Schichtung des Einheitswürfels konstruieren, indem Sie LUT-Schichten und geschlossene LUT-Schichten öffnen. Führen Sie die folgenden Schritte aus, um die Interpolation mithilfe dieser "geringen LUT-Struktur" durchzuführen. Angenommen, ein gegebener Eingabegerätwert .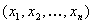

SCHRITT 1: Ermitteln der Anzahl der "aktiven" Kanäle. Dies ist die Anzahl der Nicht-Null-Kanäle. Dadurch wird die Strata-Dimension k bestimmt, um nach der enthaltenden Schicht zu suchen. Genauer gesagt ist die Strata-Dimension 3, wenn die Anzahl der aktiven Kanäle 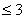, andernfalls entspricht die Strata-Dimension der Anzahl der aktiven Kanäle.

SCHRITT 2: Innerhalb 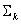, suchen Sie nach der enthaltenden Schicht. Ein Gerätewert ist in einer geöffneten Schicht enthalten, wenn alle Kanäle, die dem Stratum entsprechen, einen Wert ungleich Null aufweisen und alle anderen Kanäle null sind. Ein Gerätewert ist in einer geschlossenen Schicht enthalten, wenn jeder Kanal, der nicht durch die Schicht dargestellt wird, null ist. Wenn keine enthaltende Schicht gefunden wird, gibt es eine Fehlerbedingung. Abbrechen und Melden eines Fehlers. Wenn eine enthaltende Schicht gefunden wird, fahren Sie mit dem nächsten Schritt fort.

SCHRITT 3: Wenn die enthaltende Schicht geschlossen ist, kann die Interpolation innerhalb des Stratums durch einen bekannten Interpolationsalgorithmus erfolgen. Bei dieser Implementierung ist die Wahl des Algorithmus tetrahedrale Interpolation. Wenn die enthaltende Schicht geöffnet ist und der Gerätewert streng innerhalb des Stratums liegt, das heißt,

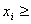ersten Knoten in i kanal

wobei i ein Kanalindex für die Stratum ist, funktioniert der Standardinterpolationsalgorithmus, z. B. tetraedrale Interpolation.

Wenn 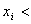ersten Knoten in i th Kanal für einige i, fällt der Gerätewert in den "Abstand" zwischen dem Stratum und den unteren dimensionalen Unterräumen. Diese MOI befasst sich nicht mit einem Interpolationsalgorithmus per se, sodass jeder Interpolationsalgorithmus verwendet werden kann, um innerhalb dieser "Lücke" interpolieren zu können, obwohl der bevorzugte Algorithmus die folgende Transfinite-Interpolation ist.

Die Architektur des Interpolationsmoduls wird in den beiden Teilen von Abbildung 1 veranschaulicht.

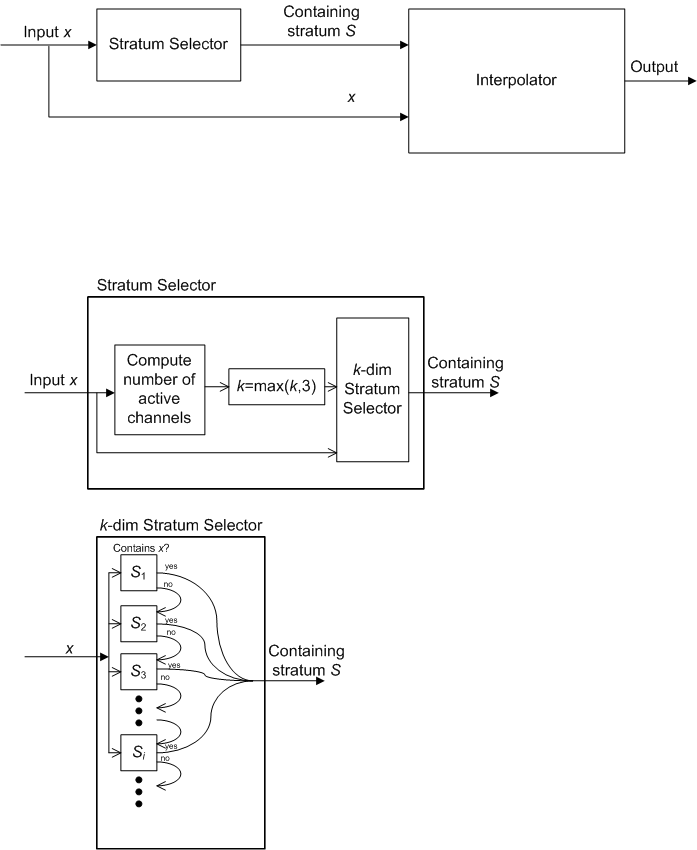
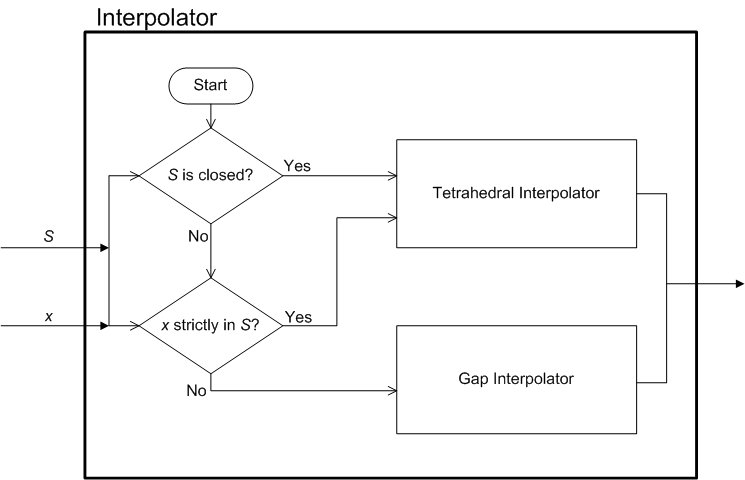
Abbildung 1: Architektur des Intepolation-Moduls

Wie bereits erwähnt, kann dieser Algorithmus in Regionen des Gerätebereichs, die wichtige Kombination aus Farbstoffen enthalten, eine relativ dichte Stichprobe erzielen und gleichzeitig die Gesamtgröße der benötigten LUTs minimieren. Die folgende Tabelle zeigt einen Vergleich der Anzahl der Knoten, die für die geringe LUT-Implementierung (mit Algorithmus #1 und normaler Modus) und der entsprechenden LUT-Implementierung erforderlich sind.

Anzahl der Eingabekanäle	sparse LUT	Uniform LUT
5	142498	1419857
6	217582	24137567
7	347444	410338673
8	559618	6975757441

 

Interpolation innerhalb eines Einheitenwürfels

Ein grundlegender Schritt im Fall eines rechteckigen Rasters ist die Interpolation innerhalb einer umschließenden Zelle. Für einen Eingabepunkt können Sie die eingeschlossene Zelle leicht bestimmen. In einem rechteckigen Raster wird der Ausgabewert an jedem Scheitelpunkt (Eckpunkte) der eingeschlossenen Zelle angegeben. Sie sind auch die einzigen Grenzbedingungen (BCs), die ein Interpolant erfüllen muss: Der Interpolant muss alle diese Punkte durchlaufen. Beachten Sie, dass sich diese Grenzbedingungen auf "diskreten" Punkten befinden, in diesem Fall die 2n Eckpunkte der Zelle, wobei n die Dimension des Farbraums ist.

Es ist nützlich, das Konzept der Grenzbedingungen zu formalisieren, bevor sie fortfahren. Für jede Teilmenge S der Grenze der eingeschlossenen Zelle (der Einheitswürfel in n Dimensionen) ist eine Begrenzungsbedingung für S eine Spezifikation einer Funktion BC: S → Rm, wobei m die Ausgabedimension ist. Mit anderen Worten, eine Interpolante, die als Interp bezeichnet werden kann: [0,1]n→ Rm, ist erforderlich, um zu erfüllen: Interp(x) = BC(x) für alle x in S.

Im Standardszenario der Interpolation auf dem Einheitswürfel ist S der Satz von einzelnen Punkten, die die 2n Scheitelpunkte des Würfels sind.

Sie können nun die Grenzbedingungen generalisieren, um die zuvor beschriebenen Probleme zu lösen und einen neuen Interpolationsalgorithmus innerhalb des Einheitenwürfels bereitzustellen. Anstatt nur diskrete Grenzpunkte zuzulassen, können Grenzbedingungen auf eine gesamte Begrenzungsseite des Würfels angewendet werden. Die genauen Annahmen sind wie folgt:

(a) Der Punkt vn =(1;1,...,1) ist speziell und nur eine diskrete Begrenzungsbedingung zulässig. Mit anderen Worten, keine fortlaufenden Grenzbedingungen können auf die n Begrenzungsflächen xi=1 (i=1,...,n) festgelegt werden.

(b) Für jede der verbleibenden n Begrenzungsflächen xi=0 (i=1,...,n) kann eine Begrenzungsbedingung auf das gesamte Gesicht festgelegt werden, wobei die Kompatibilitätsbedingung besteht, dass, wenn sich zwei Gesichter schneiden, die Grenzbedingungen auf den Gesichtern auf die Schnittmenge einigen sollten.

(c) Alle Scheitelpunkte, die nicht in den Gesichtern mit Grenzbedingung enthalten sind, haben eine individuelle (diskrete) Begrenzungsbedingung.

Sie können sich auf eine diskrete Begrenzungsbedingung als endliche Daten und eine fortlaufende Grenzbedingung als transfinitale Daten beziehen, um interpolation für endliche und transfinitale Daten zu diskutieren.

Überprüfen Sie zunächst die Standard-Tetraedral-Interpolation (z. B. die in Sakamotos Patent verwendet wurde), die dazu beiträgt, die Notationen für diese spezielle Formulierung des Problems festzulegen. Es ist bekannt, dass der Einheitswürfel [0,1]n in n unterteilt werden kann! Tetrahedra, parametrisiert durch die Gruppe von Permutationen auf n-Symbolen. Genauer gesagt, jeder solche Tetrahedron wird durch Ungleichheiten definiert

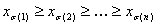
dabei ist σ:{1,2,..,n}→{1,2,...,n} eine Permutation von "Symbolen" 1, 2, ..., n, d. h. eine bijektive Zuordnung der Gruppe von n Symbolen. Wenn z. B. n = 3 und σ = (3, 2, 1), d. h. σ(1)=3, σ(2)=2, σ(3)=1, dann wird das entsprechende Tetrahedron durch z≥y≥x definiert, wobei die allgemeine Notation x, y, z für x1, x2, x3 verwendet wird. Beachten Sie, dass diese Tetrahedrons nicht voneinander getrennt sind. Für die Interpolation haben Punkte, die auf einem gemeinsamen Gesicht von zwei unterschiedlichen Tetrahedrons liegen, den gleichen Interpolationswert, unabhängig davon, welches Tetrahedron in der Interpolation verwendet wird. Bestimmen Sie im Standardszenario der Interpolation auf endlichen Punkten für einen bestimmten Eingabepunkt (x1, ..., xn), zunächst, in welchem Tetrahedron sie liegt oder in der entsprechenden Permutation σ, dann wird das Tetrahedral-Interpolant definiert als

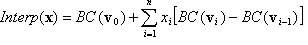
dabei zeigt 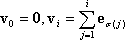für i=1, ..., n und e1, ..., en sind die Standardbasisvektoren. Bevor Sie mit der Generalisierung fortfahren, beachten Sie, dass v0, v1, ..., vn die Scheitelpunkte des Tetrahedrons sind, und 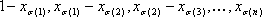sind die "baryzentrischen Koordinaten".

Für den allgemeinen Fall von BCs auf Grenzflächen können Sie das Konzept der baryzentrischen Projektion verwenden. Wie zuvor bestimmen Sie für einen bestimmten Eingabepunkt (x1, ..., xn) zuerst, in welchem Tetrahedron er liegt oder in gleicher Weise die entsprechende Permutation σ. Führen Sie dann eine Reihe baryzentrischer Projektionen wie folgt aus. Die erste projektion 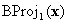sendet den Punkt an die Ebene 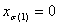, es sei denn, 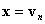in diesem Fall wird sie nicht geändert. Die genaue Definition der Karte BProj ist wie folgt definiert:

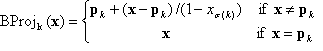
mit 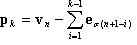und k = 1, 2, ..., n.

Im Fall 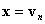, können Sie beenden, da BC in vn durch Annahme (a) definiert ist. Im Fall 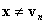, ist klar, dass 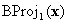hat die σ(1)th Komponente ausgelöscht. Mit anderen Worten, es befindet sich auf einer der Begrenzungsflächen. Entweder befindet es sich auf einer Oberfläche, auf der BC definiert ist, in diesem Fall können Sie anhalten, oder Sie führen eine andere baryzentrische Projektion 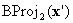wobei 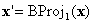. Und wenn 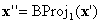sich auf einem Gesicht befindet, auf dem BC definiert ist, können Sie aufhören; andernfalls führen Sie eine weitere Projektion 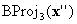. Da jede Projektion eine Komponente löscht, verringert sich die effektive Dimension, sodass Sie wissen, dass der Prozess schließlich beendet werden muss. Im schlimmsten Fall führen Sie n-Projektionen bis zur Dimension 0 durch, d. h. Scheitelpunkte auf dem Würfel, die gemäß Annahme (c) sie wissen, dass BC definiert wird.

Vorausgesetzt, dass K-Projektionen durchgeführt wurden, mit

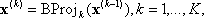
x(0)= x, der Eingabepunkt und BC werden bei x(k) definiert. Entspannen Sie dann die Projektionen, indem Sie eine Reihe von Ausgabevektoren definieren:

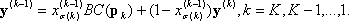
wobei 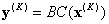, und Sie erhalten schließlich die Antwort

Beispiel für Arbeit

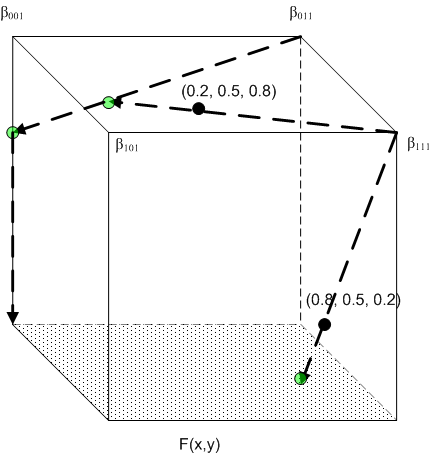
Abbildung 2: Beispiel " Gearbeitet"

Betrachten Sie die situation in Abbildung 2, wobei n = 3, m = 1, und Sie haben die folgenden BCs:

a) Vier einzelne BCs auf den Scheitelpunkten

(0, 0, 1): β001

(0, 1, 1): β011

(1, 0, 1): β101

(1, 1, 1): β111

b) Ein fortlaufender BC auf der Oberfläche x3=0: F(x1, x2)

Berechnung Nr. 1: Eingabepunkt x = (0,8, 0,5, 0,2). Das umschließende Tetrahedron ist mit der Permutation <1, 2, 3>verbunden.

1. Projektion: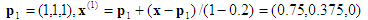

Dies befindet sich bereits auf dem Gesicht x3=0, sodass Sie aufhören können. Rückwärtsersetzung gibt dann

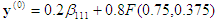, was die Antwort ist.

Berechnung #2: Eingabepunkt x = (0,2, 0,5, 0,8). Das umschließende Tetrahedron ist mit der Permutation <3, 2, 1>verbunden.

1. Projektion: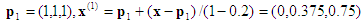

2. Projektion: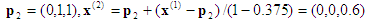

3. Projektion: 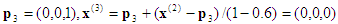, die sich auf dem Gesicht x3=0 befindet. Rückwärtsersetzung gibt dann

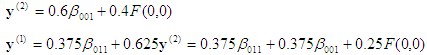
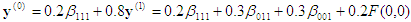, was die endgültige Antwort ist.

Anträge

(a) Sequenzielle tetrahedrale Interpolation

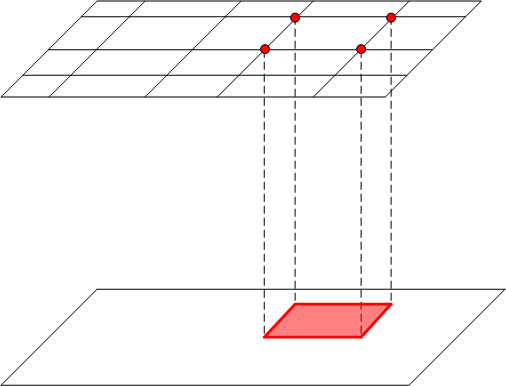
Abbildung 3: Sequenzielle tetrahedrale Interpolation

Siehe Abbildung 3. Wenn Sie zwischen zwei Ebenen interpolieren möchten, für die inkompatible Raster verhängt wurden, sollten Sie eine Zelle betrachten, die einen bestimmten Punkt P in der Abbildung einschließt. Die "oberen" Scheitelpunkte der Zelle stammen direkt aus dem Raster in der oberen Ebene. Die Scheitelpunkte im unteren Gesicht sind nicht mit dem Raster in der unteren Ebene kompatibel, sodass das gesamte Gesicht als BC mit Werten behandelt wird, die durch Interpolation im Raster in der unteren Ebene abgerufen werden. Es ist dann klar, dass diese Einrichtung Annahmen (a), (b) und (c) oben erfüllt, und Sie können den Interpolationsalgorithmus anwenden.

Es ist auch klar, dass der Algorithmus die Dimension des Interpolationsproblems um 1 reduziert hat, da das Ergebnis eine lineare Kombination von Werten an den Scheitelpunkten im oberen Raster und interpolation in der unteren Ebene ist, die Dimension weniger 1 hat. Wenn eine ähnliche Sandwichebene in der unteren Ebene vorhanden ist, können Sie das Verfahren in dieser Ebene anwenden und die Dimension um 1 weiter reduzieren. Dieses Verfahren kann fortgesetzt werden, bis Sie die Dimension 0 erreicht haben. Diese Kaskade von Projektionen und Interpolationen kann als "Sequenzielle Tetrahedral-Interpolation" bezeichnet werden.

(b) Gap Interpolation

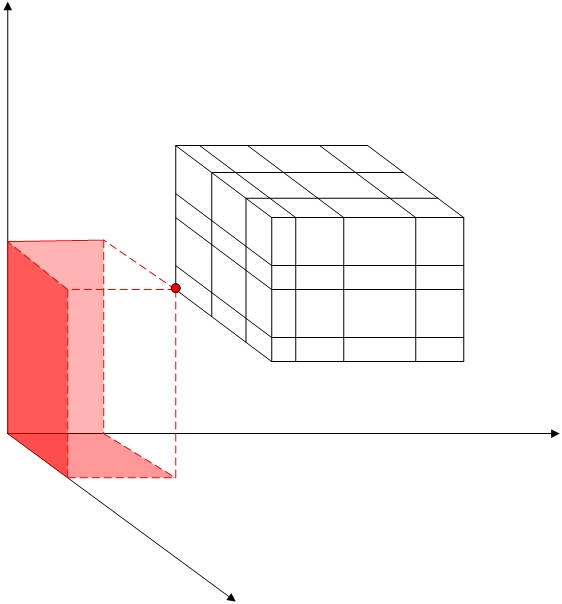
Abbildung 4: Gap-Interpolation

Dies ist ein Raster, das auf einem Würfel liegt, der streng innerhalb des positiven Quadranten sitzt. Der Würfel selbst hat ein Raster darauf, und jede Koordinatenebene verfügt über Raster, die nicht notwendigerweise kompatibel sind. Die "Lücke" zwischen dem Würfel und den Koordinatenebenen weist einen Querschnitt auf, der "L-förmig" ist und für Standardtechniken nicht amenabel ist. Mit der hier eingeführten Technik können Sie jedoch ganz einfach Zellen einführen, die diese Lücke abdecken. In Abbildung 4 ist eine dieser Abbildungen dargestellt. Die Raster auf den Koordinatenebenen unterstützen die Interpolation, die die erforderlichen BCs für alle unteren Gesichter der Zelle bereitstellt, mit einem verbleibenden Scheitelpunkt, dessen BC von der unteren Ecke des Cubes bereitgestellt wird.

Abschließender Hinweis zur Implementierung

In der tatsächlichen Anwendung wird der "Einheitswürfel", der die grundlegende Einstellung des Algorithmus ist, aus größeren Gittern extrahiert, und die Werte an den Scheitelpunkten erfordern möglicherweise eine teure Berechnung. Andererseits ist auch klar, dass die Tetrahedralinterpolation nur die Werte an den Scheitelpunkten des Tetrahedrons erfordert, was eine Teilmenge aller Scheitelpunkte des Einheitswürfels ist. Daher ist es effizienter zu implementieren, was als "verzögerte Auswertung" bezeichnet werden kann. In einer Softwareimplementierung des vorhergehenden Algorithmus ist es typisch, eine Unterroutine zu haben, die den Einheitenwürfel und die Werte an seinen Scheitelpunkten als Eingabe verwendet. Verzögerte Auswertung bedeutet, dass die erforderlichen Informationen, um die Werte der Scheitelpunkte auszuwerten, nicht an die Scheitelpunkte übergeben werden, ohne die Auswertung tatsächlich durchzuführen. Innerhalb der Unterroutine wird die tatsächliche Auswertung dieser Werte nur für die Scheitelpunkte durchgeführt, die zum eingeschlossenen Tetrahedron gehören, nachdem das umschließende Tetrahedron bestimmt wurde.

Nachschlagetabelle für die Verwendung mit virtuellen RGB-Quellgeräten mit hohem dynamischen Bereich

Wenn eine Transformation mit einem Quellgerät erstellt wird, das als virtuelles RGB-Gerät modelliert wird, ist es möglich, dass Quellfarbwerte negativ oder größer als Einheit (1,0) sein können. In diesem Fall wird das Quellgerät als hoher dynamischer Bereich (HDR) bezeichnet. Für diesen Fall wird besondere Berücksichtigung geleistet.

Bei HDR-Transformationen können die Mindest- und Höchstwerte für jeden Farbkanal anhand der Gamutgrenze des Geräts bestimmt werden. Mithilfe dieser Werte wird eine einfache Skalierung für jeden Farbkanal angewendet, sodass Farbwerte, die dem Minimalfarbstoff entsprechen, in 0,0 konvertiert werden, und Farbmittelwerte, die dem maximalen Farbmittel entsprechen, in 1,0 konvertiert werden, wobei eine lineare Skalierung von Werten zwischen 0,0 und 1,0 linear erfolgt.

ICCProfileFromWCSProfile

Da dieses Feature hauptsächlich die Unterstützung vor Vista-Versionen von Windows ist, müssen Sie Icc-Profile der Version 2.2 gemäß der Definition in ICC Specification ICC.1:1998-09 generieren. In bestimmten Fällen (siehe folgende Tabelle "Baseline Device To ICC Profile Class Mapping") können Sie eine Matrix oder ein TRC-basiertes ICC-Profil aus einem WCS-Profil erstellen. In anderen Fällen besteht das ICC-Profil aus LUTs. Im folgenden Prozess wird beschrieben, wie die AToB- und BToA-LUTs erstellt werden. Natürlich haben ICC-Profile auch andere Felder. Einige der Daten können aus dem WCS-Profil abgeleitet werden. Für andere Daten müssen Sie intelligente Standardwerte entwickeln. Das Copyright wird Microsoft zugewiesen; da es sich um eine Microsoft-Technologie handelt, die zum Erstellen der LUTs verwendet wird.

Dieses Design sollte für alle Gerätemodelle funktionieren, einschließlich Plug-Ins. Solange das Plug-In über ein zugeordnetes Basisgerätemodell verfügt, kann der zugrunde liegende Gerätetyp bestimmt werden.

Der harte Teil der Erstellung eines ICC-Profils besteht darin, die Nachschlagetabellen AToB und BToA zu erstellen. Diese Tabellen ordnen zwischen dem Geräteraum, z. B. RGB oder CMYK, und dem Profilverbindungsraum (PROFILE Connection Space, PCS) zu, bei dem es sich um eine Variante von CIELAB handelt. Dies ist im Wesentlichen identisch mit dem farbverwaltungsprozess, der in der CITE-Transformation verwendet wird, um vom Geräteraum zum Gerätebereich zuzuordnen. Sie müssen jedoch über die folgenden Informationen verfügen, um die Transformation vorzunehmen.

1. Referenzanzeigebedingungen für pcS.

2. Referenz-PCS-Gamut.

3. Gerätemodell, das zwischen PCS-Werten und Colorimetrie konvertiert wird.

Das WCS-Profil und die zugehörige CAM werden als Parameter bereitgestellt. Es gibt zwei grundlegende Gerätemodelle, die zwischen Colorimetrie und PCS-Codierung konvertieren. Der Grund, warum Sie zwei benötigen, wird unten erläutert.

1. Sie können die Referenzanzeigebedingungen für die PCS aus der ICC-Profilformatspezifikation abrufen. Die in der ICC-Profilformatspezifikation bereitgestellten Informationen reichen aus, um alle daten zu berechnen, die zum Initialisieren der vom CMS verwendeten CAM erforderlich sind. Für Konsistenz und Flexibilität werden diese Informationen in einem WCS-Farbprofil gespeichert.

2. Sie können auch ein WCS-Profil verwenden, um Beispiele zu speichern, die die Referenzskala des PCS definieren. Das CITE-Farbmanagementsystem (CMS) verfügt über zwei Möglichkeiten zum Erstellen von Gamutgrenzen. Eine besteht darin, den vollständigen Gerätebereich zu probieren und das Gerätemodell zum Erstellen von Messwerten zu verwenden. Die zweite Methode besteht darin, gemessene Stichproben aus dem Profil zu verwenden, um eine Bezugsskalagrenze zu erstellen. Da die Gamut des ICC PCS zu groß ist, um eine nützliche Referenzskala zu machen, ist die erste Methode ungeeignet. Die zweite Methode ist jedoch ein flexibler, profilbasierter Ansatz. Um die Referenz-PCS-Gamut neu zu definieren, können Sie die Messdaten im PCS-Geräteprofil ändern.

3. Der ICC PCS ist eine Modellierung eines idealen Geräts. Durch die Erstellung eines Modells von PCS als echtes Gerät können Sie den farbverwaltungsprozess nutzen, der im Smart CMM verwendet wird. Das Erstellen eines Gerätemodells von colorimetry bis zur PCS-Codierung ist einfach. Sie ordnen einfach zwischen den tatsächlichen Farbmetrikwerten und den PCS-codierten Werten zu. Da die CMS-Schnittstelle für Gerätemodelle nur XYZ-Werte unterstützt, müssen Sie möglicherweise auch zwischen XYZ und LAB zuordnen. Dies ist eine bekannte Transformation. Dieses Modell wird in den Abschnitten 7.9 und 7.10 im Dokument 2.2.02 "Baseline Device Models" beschrieben.

Möglicherweise müssen Sie eine Gamutzuordnung durchführen, wenn die Gamut des Geräts größer als die Gamut der PCS ist. Die Basis-GVO können zu diesem Zweck verwendet werden. Beachten Sie, dass ein ordnungsgemäß erstelltes ICC-Profil Nachschlagetabellen für die Absichten "Relative Colorimetric", "Perceptual" und "Sättigung" enthält, obwohl diese intern auf denselben LUT verweisen können.

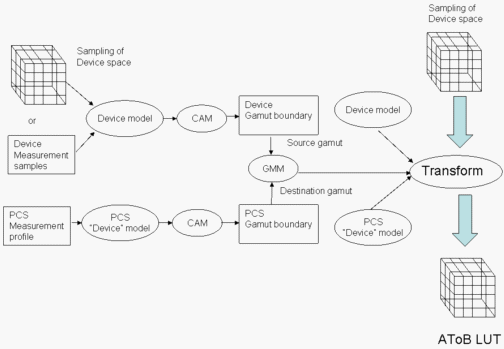
Abbildung 5: Erstellung eines AToB-LUT

Dieser Vorgang ist in Abbildung 5 dargestellt. Zunächst wird das Gerätemodell aus den Daten im DM-Profil initialisiert. Erstellen Sie dann wie folgt eine Geräteskalagrenze. Ein Sampling von Daten aus dem Gerätemodell wird über das Gerätemodell ausgeführt, um farbmetrische Daten abzurufen. Die farbmetrischen Daten werden über die CAM ausgeführt, um Darstellungsdaten zu erstellen. Die Darstellungsdaten werden verwendet, um die Geräteskalagrenze zu erstellen.

Verwenden Sie als Nächstes Daten aus dem Referenz-PCS-Messprofil, um eine Gamutgrenze für den PCS zu erstellen.

Verwenden Sie die beiden soeben erstellten Gamut-Grenzen, um ein GMM zu initialisieren. Verwenden Sie dann das Gerätemodell, das GMM und das PCS-Gerätemodell, um eine Transformation zu erstellen. Führen Sie ein Sampling des Gerätebereichs durch die Transformation aus, um einen AToB-LUT zu erstellen.

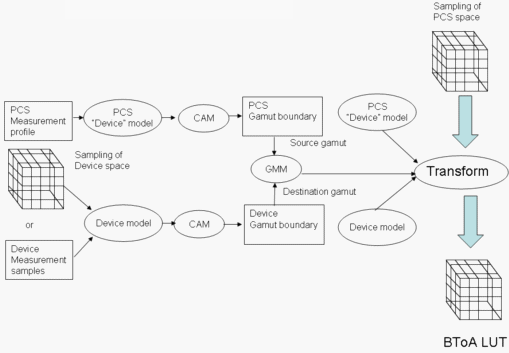
Abbildung 6: Erstellung eines BToA LUT

Abbildung 6 veranschaulicht die Erstellung des BToA LUT. Dies ist fast identisch mit der Erstellung eines AToB LUT, wobei die Rollen des Quell- und Zielaustauschs ausgetauscht werden. Außerdem müssen Sie die vollständige PCS-Gamut zum Erstellen der LUT beispielen.

Beachten Sie, dass die CAM (CIECAM02 in WCS) an dem Prozess beteiligt ist, die farbtische Anpassung zwischen dem Medienweißpunkt und dem PCS-Weißpunkt (von ICC als D50 vorgeschrieben) transparent von der CAM beeinflusst wird.

VIRTUELLE RGB-HDR-Geräte

Besondere Berücksichtigung bei der Generierung von Profilen für virtuelle HDR-RGB-Geräte; d. h. Geräte, für die die Farbwerte kleiner als 0,0 oder größer als 1,0 sein können. In der Generation des ATOB LUT wird ein größerer Satz von 1D-Eingabe-LUTs erstellt. Farbwerte werden skaliert und in den Bereich 0 versetzt. 1 unter Verwendung der minimalen und maximalen Farbwerte im WCS-Profil.

Da der Farbraum für HDR-Geräte wahrscheinlich nicht vollständig aufgefüllt wird, wird auch im 3D-LUT für das Tag spezielle Unterstützung bereitgestellt. Um Farben im dünn gefüllten Bereich zu behandeln, werden die Farbmittel neu codiert, sodass die Extrapolation über 0,0 und 1,0 erreicht werden kann. Der verwendete Bereich ist -1 .. +4.

Aufgrund der für die 3D-LUT angewendeten Reskalierung wird eine Reihe von 1D-Ausgabe-LUTs erstellt, um das Ergebnis dem Bereich 0 zuzuordnen. 1.

Mehr als ein PCS

Der ICC stellte fest, dass ein PCS nicht ausreichend flexibel war, um alle beabsichtigten Verwendungen eines CMS zu erfüllen. In Version 4 der Profilspezifikation hat der ICC klargestellt, dass es tatsächlich zwei PCS-Codierungen gibt. Eine wird für die farbmetrischen Absichten verwendet; eine andere wird für die wahrnehmungsbezogene Absicht verwendet. (Für die Sättigungsabsicht ist kein PCS angegeben. Der ICC hat diesen Teil mehrdeutig gelassen.) Der farbmetrische PCS hat eine minimale und maximale Helligkeit angegeben, aber die Farb- und Farbtonwerte reichen bis zu etwa ± 127. Dieser PCS sieht wie ein rechteckiges Prisma aus. Wie bereits erwähnt, ähnelt das wahrnehmungsbezogene PCS-Volumen der Gamut eines Tintenstrahldruckers.

Die beiden ICC-PCS verfügen ebenfalls über zwei verschiedene digitale Codierungen. Im wahrnehmungsbezogenen PCS stellt ein Wert von Null eine Lichtheit von Null dar. Im farbmetrischen PCS stellt ein Wert von Null die minimale Lichtheit des PCS dar, der größer als 0 ist. Sie können dieses Problem lösen, indem Sie für jede PCS-Codierung ein anderes Gerätemodell verwenden.

Gamut-Zuordnung

Um die AToB-LUTs in einem ICC-Profil zu erstellen, ordnen Sie die Geräteskala dem entsprechenden PCS-Raum zu. Um die BToA-LUTs zu erstellen, ordnen Sie vom PCS-Raum zur Geräteskala zu. Die Zuordnung der AToB-LUTs ist ähnlich wie bei einem messbasierten CMS. Ordnen Sie für die wahrnehmbaren PCS die Plausible Gamut des Geräts der perceptualEN PCS-Gamutgrenze zu, indem Sie entweder Clipping oder Komprimierung für alle Out-of-Gamut-Farben verwenden. Für die farbmetrischen Absichten müssen Sie möglicherweise Helligkeit abschneiden, aber die Farbtonwerte passen alle in die farbmetrische PCS-Gamut.

Die Zuordnung für die BToA-LUTs unterscheidet sich etwas. Die farbmetrischen Absichten sind immer noch einfach; Sie schneiden einfach PCS-Werte auf die Geräteskala ab. Der ICC erfordert jedoch, dass alle möglichen PCS-Werte einem bestimmten Gerätewert zugeordnet sind, nicht nur die innerhalb der Referenzskala des wahrnehmungsbezogenen PCS. Daher müssen Sie sicherstellen, dass die GMMs Quellfarben verarbeiten können, die sich außerhalb der Referenzskala befinden. Dies kann durch Beschneiden dieser Farben an die Grenzen der Geräteskala behandelt werden.

Basisgerät zur ICC-Profilklassenzuordnung

Basisgerätetyp	ICC-Profilklasse	Bemerkung
RGB-Aufnahmegerät	Eingabegerät ("scnr")	PCS ist CIELAB. AToB0Tag ist Device to PCS mit relativer farbmetrischer Absicht.
CRT, LCD-Monitor	Anzeigegerät ("mntr")	PCS ist CIEXYZ. Informationen zur Modellkonvertierung finden Sie im Folgenden.
RGB-Projektor	Farbraum ("Abstand")	PCS ist CIELAB.
RGB- und CMYK-Drucker	Ausgabegerät ("prtr")	PCS ist CIELAB.
VIRTUELLEs RGB-Gerät (Nicht-HDR-Fall)	Anzeigegerät ("mntr")	PCS ist CIEXYZ.
VIRTUELLEs RGB-Gerät (HDR-Fall)	Farbraum ("Abstand")	PCS ist CIELAB.

 

Die Umwandlung von Monitorprofilen umfasst nicht das Erstellen von LUTs, sondern besteht stattdessen aus dem Erstellen einer Matrix oder eines TRC-Modells. Das in ICC verwendete Modell unterscheidet sich geringfügig von dem modelliert, das in der WCS CRT- oder LCD-Modellierung verwendet wird, da der Begriff "Schwarze Korrektur" fehlt. Nämlich

WCS-Modell: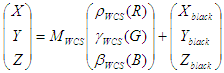

ICC-Modell: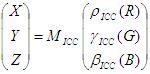

Die Konvertierung vom WCS-Modell in das ICC-Modell erfolgt wie folgt.

Definieren neuer Kurven:

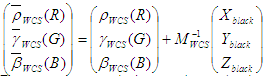
Dies sind keine Tonwiedergabekurven, da sie nicht 1 bis 1 zuordnen. Eine Normalisierung wird dies erreichen. Die endgültigen Definitionen des ICC-Modells sind:

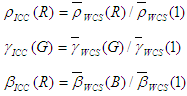
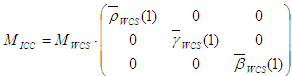
Für virtuelle Nicht-HDR RGB-Geräte generieren Sie auch ein ICC-Displayprofil für die Raumeffizienz. In diesem Fall kann die Tristimulus-Matrix M ICC direkt aus den Primaren des WCS-Profils ohne die oben genannte Modellkonvertierung abgerufen werden. Eine letzte, aber wichtige Anmerkung ist, dass diese Tristimulus-Matrix chrommatisch an D50 angepasst werden muss, um die ICC-Spezifikation des PCS zu erfüllen. Mit anderen Worten, die Einträge in jeder Zeile der Matrix, die im ICC-Profil codiert werden sollen, müssen jeweils 96.42, 100 und 82.49 addiert werden. In der aktuellen Implementierung erfolgt die chromatische Anpassung durch CAT02, die auch die in CAM02 verwendete chromatische Anpassungstransformation ist.

Schwarze Erhaltung und Schwarze Generation

Die Implementierung der schwarzen Erhaltung ist mit der Generation des schwarzen Kanals in Geräten verbunden, die einen schwarzen Kanal unterstützen. Dazu werden Informationen zu jeder Quellfarbe gesammelt, um Gerätemodelle zu ermöglichen, die einen schwarzen Kanal unterstützen, um zu bestimmen, wie sie den schwarzen Kanal bei der Ausgabe am besten festlegen können. Während die schwarze Erhaltung für Farbtransformationen relevant ist, die zwischen einem Schwarzkanalgerät in ein anderes konvertiert werden, wird die schwarze Generation für alle Transformationen implementiert, die ein Zielgerät mit schwarzem Kanal umfassen.

Informationen zu schwarzen Kanälen werden in einer Datenstruktur mit dem Namen BlackInformationaufgezeichnet. Die BlackInformation--Struktur enthält einen booleschen Wert, der angibt, ob die Farbe nur schwarze Farbe und einen numerischen Wert enthält, der den Grad der "Schwarzstärke" angibt. Bei Quellgeräten, die einen schwarzen Kanal unterstützen, ist die schwarze Gewichtung der Prozentsatz der schwarzen Farbe in der Quellfarbe. Bei Quellgeräten, die keinen schwarzen Kanal enthalten, wird die schwarze Gewichtung mit den anderen Farbstoffen und dem Darstellungswert berechnet. Ein Wert namens "Farbreinheit" wird berechnet, indem der Unterschied zwischen dem maximalen Farbwert und dem minimalen Farbwert dividiert durch den maximalen Farbwert verwendet wird. Ein Wert namens "relative Lichtheit" wird berechnet, indem der Unterschied zwischen der Lichtheit der Farbe und der Minimallichtigkeit für das Zielgerät dividiert durch den Unterschied zwischen dem Minimal- und dem maximalen Lichtwert für das Zielgerät geteilt wird. Wenn es sich bei dem Quellgerät um ein additives Gerät (Monitor oder Projektor) handelt, wird das schwarze Gewicht als 1,0 minus die Farbreinheit bestimmt, die durch die relative Lichtstärke multipliziert wird. Wenn das Quellgerät beispielsweise ein RGB-Monitor ist, wird der Maximalwert und der Minimalwert von R, G und B für jede Farbe berechnet, und die schwarze Gewichtung wird durch die Formel bestimmt:

BW = (1,0 – (max(R,G,B) – min(R,G,B)) / max(R, G, B)) * relative Lichtheit

Wenn das Quellgerät subtrahierende Farben unterstützt, z. B. einen CMY-Drucker, müssen die einzelnen Farbmittel "ergänzt" sein (subtrahiert von 1,0), bevor sie in der vorherigen Formel verwendet werden. Daher gilt für einen CMY-Drucker R = 1,0 – C, G = 1,0 – M und B = 1,0 – Y.

Die schwarzen Informationen für jede von der Farbtransformation verarbeitete Farbe werden während des Farbübersetzungsprozesses bestimmt. Die Nur-Schwarz-Informationen werden nur bestimmt, wenn die schwarze Erhaltung angegeben ist. Die schwarze Gewichtung wird immer bestimmt, wenn das Zielgerätemodell einen schwarzen Farbstoff unterstützt. Die schwarzen Informationen werden über die ColorimetricToDeviceColorsWithBlack-Methode an das Zielgerätemodell übergeben, die die resultierende LUT verwendet.

Beachten Sie, dass der obige Prozess aufgrund der Farbtransformationsoptimierung nur während der Erstellung der optimierten Transformation LUT erfolgt, nicht während der Ausführung der TranslateColors-Methode.

Optimierung für Transformationen mit mehr als drei Quellkanälen

Die Größe der optimierten Transformation wird durch mehrere Faktoren bestimmt: die Anzahl der Farbkanäle im Quellgerät, die Anzahl der Schritte in der Tabelle für jeden Quellfarbkanal und die Anzahl der Farbkanäle im Ausgabegerät. Die Formel zum Bestimmen der Größe der Transformationstabelle lautet:

Größe = Anzahl der Schritte pro Kanal _{Quelle\ Gerät(Anzahl\ kanäle\ in\ Quelle\ Gerät)} x Anzahl der Kanäle im Ausgabegerät

Wie Sie sehen können, wächst die Größe der Tabelle exponentiell, abhängig von der Anzahl der Kanäle im Quellgerät. Viele Quellgeräte unterstützen drei Farbkanäle, z. B. Rot, Grün und Blau. Wenn ein Quellgerät jedoch vier Kanäle unterstützt, z. B. CMYK, wird die Größe der Tabelle und die zum Erstellen der Tabelle erforderliche Zeit um einen Faktor der Anzahl der Schritte vergrößert. In einem messbasierten CMS, bei dem Transformationen "on the fly" konstruiert werden, kann dieses Mal gut inakzeptabel sein.

Um die zum Konstruieren der Farbkonvertierungstabelle erforderliche Zeit zu reduzieren, ist es möglich, zwei Fakten zu nutzen. Erstens, während das Quellgerät mehr als drei Farbkanäle unterstützt, verfügt der zwischengeschaltete geräteunabhängige Farbraum (CIECAM02 Ja _C b _C ) nur über drei Farbkanäle. Zweitens ist der zeitaufwändige Teil der Verarbeitung nicht die Gerätemodellierung (Konvertierung von Gerätefarbkoordinaten in Tristimulus-Werte), sondern die Gamutzuordnung. Mithilfe dieser Fakten können Sie eine vorläufige Farbkonvertierungstabelle erstellen, die Farben im geräteunabhängigen Farbraum über die Schritte zur Gamutzuordnung und schließlich über das Farbmodell des Ausgabegeräts konvertiert. Die Konstruktion dieser Tabelle ist von Dimension 3. Anschließend konstruieren wir die vier endgültige Farbkonvertierungstabelle, indem wir die Quellfarbkombinationen in zwischengeschalteten geräteunabhängigen Raum konvertieren und dann mithilfe der vorläufigen Farbkonvertierungstabelle die Konvertierung in den Farbraum des Ausgabegeräts abschließen. Daher reduzieren Sie die Berechnung (Anzahl der Schritte in der Nachschlagetabelle) _{Anzahl\ von\ Kanälen} Gamut-Zuordnungsberechnungen auf die Anzahl der Schritte in der Zwischentabelle ₃ Gamut-Zuordnungsberechnungen. Obwohl Sie die Anzahl der Schritte in der (Nachschlagetabelle) _{Anzahl\ von\ Kanälen} Berechnungen von Gerätemodellierung und dreidimensionalen Tabellensuche ausführen müssen, ist dies immer noch viel schneller als die ursprüngliche Berechnung.

Der vorstehende Prozess funktioniert gut, vorausgesetzt, dass es keine Notwendigkeit gibt, Informationen zwischen dem Quellgerätemodell und anderen Komponenten in der Farbtransformation zu übergeben. Wenn das Ausgabegerät und das Quellgerät jedoch beide einen schwarzen Farbstoff unterstützen und beim Bestimmen des Schwarzen Ausgabefarbstoffs die quellschwarzen Informationen nicht ordnungsgemäß kommunizieren. Ein alternativer Prozess besteht darin, eine vorläufige Farbkonvertierungstabelle zu erstellen, die Farben im geräteunabhängigen Farbraum nur über die Schritte zur Gamutzuordnung konvertiert. Erstellen Sie dann die letzte Farbkonvertierungstabelle mit den folgenden Schritten: a) konvertieren Sie die Quellfarbkombinationen in zwischengeschalteten geräteunabhängigen Raum, b) führen Sie die Gamutzuordnungsschritte aus, indem Sie in der vorläufigen Farbtabelle interpolieren, anstatt die tatsächlichen Gamut-Zuordnungsprozesse anzuwenden, und c) verwenden Sie die resultierenden Werte aus den Schritten für die Gamutzuordnung und alle Quell-Schwarzkanalinformationen, um die Ausgabegerätefarbstoffe mithilfe des Ausgabegerätemodells zu berechnen. Dieser Prozess kann auch verwendet werden, wenn Informationen zwischen den Quell- und Ausgabegerätemodellen übertragen werden, auch wenn kein schwarzer Kanal vorhanden ist. Beispiel: Wenn die beiden Module mit einer Plug-In-Architektur implementiert werden, die den Datenaustausch zwischen Modulen ermöglicht.

Die beiden vorhergehenden Prozesse können verwendet werden, um die zum Erstellen der vierdimensionalen Farbtransformationstabelle erforderliche Zeit effektiv zu verbessern.

CheckGamut

ICM ruft CreateTransform auf und CreateMultiProfileTransform nehmen ein Wort mit Flagwerten, von denen einer ENABLE_GAMUT_CHECKING ist. Wenn dieses Kennzeichen festgelegt ist, muss CITE die Transformation anders erstellen. Die ersten Schritte sind identisch: Die Quell- und Zielzertifizierungsstellen müssen initialisiert werden, dann müssen die Quell- und Ziel-Gamut-Begrenzungsdeskriptoren initialisiert werden. Unabhängig von der angegebenen Absicht muss die CheckGamut GMM verwendet werden. Die CheckGamut GMM sollte mithilfe der Quell- und Zielgerätemodelle und Gamut-Begrenzungsdeskriptoren initialisiert werden. Die Transformation sollte dann jedoch eine abgeschnittene Transformation erstellen, die das Quellgerätemodell, die Quell-CAM, alle dazwischen liegenden GMMs und die CheckGamut GMM umfasst. Dadurch wird sichergestellt, dass die Ausgabe der Delta-Werte J, Delta C und Delta h vom CheckGamut CMM zu den endgültigen Ergebniswerten wird.

Die Bedeutung von CheckGamut ist klar, wenn nur zwei Geräteprofile in der Transformation vorhanden sind. Wenn mehr als zwei Geräteprofile und mehr als zwei GMMs vorhanden sind, meldet CheckGamut, ob die Farben, die durch das erste Gerätemodell transformiert wurden, und alle, aber das letzte GMM in die Gamut des Zielgeräts fallen.

Verwandte Themen

Grundlegende Farbverwaltungskonzepte

Windows-Farbsystemschemas und Algorithmen