WCS-Farbauswahlpalette: Profilschema und Algorithmen
- Übersicht
- Architektur des Gamut-Kartenmodellprofils
- Generierung der Gamut-Grenze
- Das GMMP-Schema
- Die GMMP-Schemaelemente
- GamutMapModel
- GmMP-Baselinealgorithmen
- Ausrichten der Neutralachsen
-
Gamut Boundary Description and Gamut Shell Algorithms
- Triangulation der Gamut-Grenze
- Begrenzungslinienelemente
- Gamut-Vorgang: CheckGamut
- Ebene des gesamten Farbtons: Schnitt schneiden
- Gamut-Vorgang: CheckGamut (Fortsetzung)
- Zuordnung des Mindestfarbunterschieds
- Farbtonglättung
- Festlegen von Vor- und Sekundärdateien in der Beschreibung der Gamut-Begrenzung
- Festlegen der neutralen Achse in der Beschreibung der Gamut-Begrenzung
- Zugehörige Themen
Übersicht
Dieses Schema wird verwendet, um den Inhalt eines GAMUT-Kartenmodellprofils (GMMP) anzugeben. Die zugehörigen Baselinealgorithmen werden im folgenden Thema beschrieben.
Das grundlegende GMMP-Schema besteht aus allgemeinen Headerinformationen, einem optionalen Verweis auf ein bevorzugtes Gamut Map Model-Plug-In und Erweiterungstags.
Darüber hinaus stellt der GMMP explizite Informationen zum zielorientierten Gamut-Kartenmodell bereit und stellt eine Richtlinie für das Geplante Fallback-Gamut-Kartenmodell bereit, das verwendet werden soll, wenn das Zielmodell nicht verfügbar ist. Das Schema kann private Erweiterungsinformationen enthalten, enthält aber keine anderen zusätzlichen Informationen.
Architektur des Gamut-Kartenmodellprofils
Die Stichprobenentnahme des Farbmittelraums des Ausgabegeräts erfolgt durch das Durchlaufen der Farbmittel von 0,0 auf 1,0 mit einem Bruchschritt, das Sammeln aller Kombinationen der einzelnen Farbmittel in jedem Schritt und anschließendes Konvertieren vom Gerätefarbstoffraum in den Farbbereich mit der DM::D eviceToColorimetricColors-Methode gefolgt von der CAM::ColorimetricToAppearanceColors-Methode. Im Folgenden finden Sie ein Beispiel dafür, wie dies für RGB geschieht.
For (red= 0.0; red <= 1.0; red += redStep) {
For (green = 0.0; green <= 1.0; green += greenStep) {
For (blue = 0.0; blue <= 1.0; blue += blueStep) {
Colorants[0] = red; colorants[1] = green; colorants[2] = blue;
pRGBDM->DeviceToColorimetricColors(1, colorants, &XYZ);
pCAM->ColorimetricToAppearanceColors(1, &XYZ, &JCh);
}
}
}
Generierung der Gamut-Grenze
Es gibt drei Komponenten für die Gamutgrenze: die Vorwahlen, die neutralen Proben und die Shells. Die Vorwahlen werden generiert, indem die Geräteprimries verwendet und die Transformation DeviceToColorimetric/ColorimetricToAppearance angewendet wird. Die neutralen Proben werden generiert, indem der Gerätefarbstoffraum im neutralen Bereich abtastet und dieselbe Transformation angewendet wird. Für drei Farbstoffgeräte (RGB oder CMY) sind die neutralen Proben so definiert, dass alle Farbmittel gleich sind, z. B. R == G == B. Für CMYK sind die neutralen Proben als mit C == M == Y == 0 definiert.
Die Faktoren, die die Zum Erstellen der Gamutgrenze verwendeten Daten beeinflussen, sind die Datenbeispiele (nur Baselinegeräte) und die Anzeigebedingungen. Die Schrittgröße, die zum vollständigen Sampling des Farbmittelraums (für Monitore und für plausible Shell) verwendet wird, ist eine interne Konstante und steht nicht für externe Manipulationen zur Verfügung. Das Ändern der Anzeigebedingungen ändert das Verhalten des Farbdarstellungsmodells (CAM) und die Form der Gamutgrenze, sodass Sie eine Angrenzung des Bereichs generieren müssen, die an das Profil der Anzeigebedingungen gebunden ist. Wenn Beispieldaten wie bei Basisdruckern und Erfassungsgeräten verwendet werden, haben die Beispiele große Auswirkungen auf die Form des Referenzumfangs und wirken sich auf das Verhalten des Modells selbst aus.
Für Eingabegeräte, wie Kameras und Scanner, werden verschiedene Samplings verwendet, um die Referenzshell und die plausible Shell zu generieren. Die Verweisshell wird aus den Messungen generiert, die zum Initialisieren des Gerätemodells verwendet werden. Die plausible Shell wird ähnlich der vorherigen Abbildung für Ausgabegeräte generiert. Der Unterschied: Wenn Sie ein typisches Ziel eingeben, erhalten Sie keine vollständig gesättigten Werte (wobei R, G oder B = 255). Sie müssen mithilfe des Gerätemodells extrapolieren, um diese Werte zu schätzen.
Das GMMP-Schema
<?xml version="1.0" encoding="UTF-8"?>
<xs:schema
xmlns:gmm="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"
xmlns:wcs="http://schemas.microsoft.com/windows/2005/02/color/WcsCommonProfileTypes"
targetNamespace="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"
xmlns:xs="http://www.w3.org/2001/XMLSchema"
elementFormDefault="qualified"
attributeFormDefault="unqualified"
blockDefault="#all"
version="1.0">
<xs:annotation>
<xs:documentation>
Gamut Map Model profile schema.
Copyright (C) Microsoft. All rights reserved.
</xs:documentation>
</xs:annotation>
<xs:import namespace="http://schemas.microsoft.com/windows/2005/02/color/WcsCommonProfileTypes" />
<xs:element name="GamutMapModel">
<xs:complexType>
<xs:sequence>
<xs:element name="ProfileName" type="wcs:MultiLocalizedTextType"/>
<xs:element name="Description" type="wcs:MultiLocalizedTextType" minOccurs="0"/>
<xs:element name="Author" type="wcs:MultiLocalizedTextType" minOccurs="0"/>
<xs:element name="DefaultBaselineGamutMapModel">
<xs:simpleType>
<xs:restriction base="xs:string">
<xs:enumeration value="HPMinCD_Absolute"/>
<xs:enumeration value="HPMinCD_Relative"/>
<xs:enumeration value="SGCK"/>
<xs:enumeration value="HueMap"/>
</xs:restriction>
</xs:simpleType>
</xs:element>
<xs:element name="PlugInGamutMapModel" minOccurs="0">
<xs:complexType>
<xs:sequence>
<xs:any namespace="##other" processContents="skip"
minOccurs="0" maxOccurs="unbounded" />
</xs:sequence>
<xs:attribute name="GUID" type="wcs:GUIDType" use="required"/>
</xs:complexType>
</xs:element>
</xs:sequence>
<xs:attribute name="ID" type="xs:string" use="optional" />
</xs:complexType>
</xs:element>
</xs:schema>
Die GMMP-Schemaelemente
GamutMapModel
Dieses Element ist eine Sequenz der folgenden Unterelemente:
- ProfileName-Zeichenfolge,
- DefaultBaselineGamutMapModel,
- Optionale Beschreibungszeichenfolge,
- Optionale Autorenzeichenfolge,
- Optionale PlugInGamutMap und
- Optionaler ExtensionType.
Validierungsbedingungen : Jedes Unterelement wird durch seinen eigenen Typ überprüft.
Namespace
xmlns:gmm="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"
targetNamespace="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"
Version
Version "1.0" mit der ersten Version von Windows Vista.
Validierungsbedingungen : 1.0 in Windows Vista. Versionen <2.0 sind auch gültig, um unterbrechungsfreie Änderungen am Format zu unterstützen.
Dokumentation
Schema des Gamut-Kartenmodellprofils.
Copyright (C) Microsoft. Alle Rechte vorbehalten.
Validierungsbedingungen : Jedes Unterelement wird durch seinen eigenen Typ überprüft.
DefaultBaselineGamutMapModel-Typ
UINT-Typ
Enumerationswerte:
- "MinCD\_Absolute" "MinCD\_Relative" "SIG\_KNEE" "HueMap"
Validierungsbedingungen : Die Werte müssen mit einer der obigen Enumerationen übereinstimmen.
PlugInGamutMapType
Dieses Element ist eine Sequenz eines GUIDType-Typs und aller Unterelemente.
Validierungsbedingungen : Die GUID wird verwendet, um der GMM PlugIn DLL GUID zu entsprechen. Es gibt maximal 100.000 benutzerdefinierte Unterelemente.
ExtensionType
Dieses Element ist eine optionale Sequenz beliebiger Unterelemente.
Validierungsbedingungen : Es können maximal 100.000 Unterelemente vorhanden sein.
GmMP-Baselinealgorithmen
Ausrichten der Neutralachsen
Die meisten Gamut-Zuordnungsalgorithmen haben das Ziel, die neutrale Achse des Quellgeräts der neutralen Achse des Zielgeräts zuzuordnen: Das heißt, weiß wird zu weiß, schwarz zu schwarz und grau zu grau. Dies wird teilweise durch Skalieren der Helligkeit der Quellfarben an den Helligkeitsbereich des Zielgeräts behoben. Doch damit wird das Problem nicht vollständig gelöst.
Es ist eine physische Eigenschaft der meisten Bildgeräte, dass die Farbigkeit des Geräts Weiß nicht genau mit der Farbigkeit des Geräts Schwarz übereinstimmt. Monitorweiß hängt beispielsweise von der Summe der Chromatitäten und relativen Leuchtdichten der drei Vorwahlen ab, während Monitorschwarz von der Reflektion der Anzeigeoberfläche abhängt. Drucker weiß hängt von der Farbigkeit des Papiers ab, während der Drucker schwarz von der verwendeten Tinte oder dem verwendeten Toner abhängt. Ein Darstellungsmodell, das das Weiß des Geräts exakt der neutralen Achse des Erscheinungsbildraums (Chroma genau gleich 0) zuordnet, ordnet der neutralen Achse das Schwarz des Geräts nicht zu. Da das Auge mit zunehmender Helligkeit empfindlicher auf Chromaunterschiede reagiert, werden Mittelgraue als noch chromatischer dargestellt als Geräteschwarz. (Abbildung 1 veranschaulicht die Krümmung der Neutralachsen in zwei Dimensionen. Tatsächlich bilden die Neutralachsen eine komplexere Kurve in drei Dimensionen.)
Während die CAM vorhersagt, dass diese geräteneutralen Farben chromatisch erscheinen, scheinen die tatsächlichen Beobachter dies zu kompensieren. Die meisten Menschen betrachten diese geräteneutralen Werte nicht als chromatisch. Für die meisten Gamut-Zuordnungsmodelle sollten Sie daher weiterhin quellneutrale Geräte zuordnen.
Um quellneutrale Elemente geräteneutral zuzuordnen, passen Sie die Grenzen des Quell- und Zielraums sowie jedes Pixel an, wenn Sie den Algorithmus für die Gamutzuordnung anwenden. Passen Sie zunächst jeden Wert in der Quellfarbe so an, dass die neutrale Achse des Quellgeräts in der Quellfarbe direkt auf die neutrale Achse des Erscheinungsbildraums fällt. (Siehe die linke Seite von Abbildung 1.) Passen Sie dann die Beschreibung der Gamutgrenze des Zielgeräts so an, dass die Helligkeit jeder Farbe auf der neutralen Achse des Zielgeräts an der Zielgeräteskamutgrenze direkt auf die neutrale Achse des Darstellungsraums fällt. (Siehe die rechte Seite von Abbildung 1.)
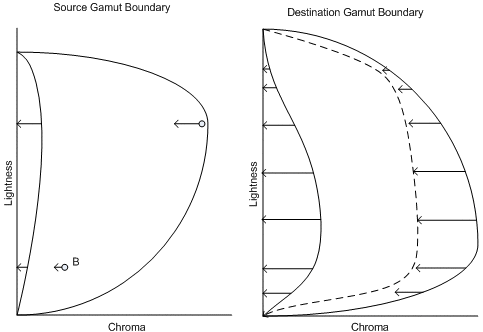
Abbildung 1 : Ausrichtung der neutralen Achsen dargestellt. Links: Anpassen von Quellpunkten relativ zur neutralen Achse des Quellgeräts. Rechts: Anpassen der Beschreibung der Zielskamutgrenze relativ zur Beschreibung der Zielraumgrenze.
Beachten Sie, dass Sie jeden Quellpixelwert relativ zur neutralen Achse an diesem Helligkeitswert anpassen. Dadurch wird sichergestellt, dass neutrale Quellgeräte auf die neutrale Achse des Darstellungsmodells fallen. Sie verschieben auch alle anderen Farben bei dieser Leichtigkeit um die gleiche Menge, sodass es keine Diskontinuitäten bei der Darstellung des Quellraums gibt. Sie müssen um unterschiedliche Mengen bei unterschiedlichen Helligkeitsstufen verschieben, da die neutralen Quellgeräte bei den verschiedenen Helligkeitsstufen nicht als gleich chromatisch dargestellt werden. Natürlich ist dies keine triviale Transformation.
Die Verarbeitung der Zielgerätewerte ist etwas schwieriger. Zunächst passen Sie die gesamte Zielraumgrenze auf ähnliche Weise an, jedoch relativ zur neutralen Zielachse. Dies ist in Abbildung 1 auf der rechten Seite dargestellt. Durch diese Anpassung wird sichergestellt, dass die Quellgrauwerte den Grauwerten des Ziels zugeordnet werden. Dies ist der Raum, in dem die Gamutzuordnungsalgorithmen funktionieren.
Dieser Bereich beschreibt jedoch nicht genau das wahre Verhalten des Zielgeräts. Sie müssen die Zuordnung umkehren, bevor dem Darstellungsmodell und dem Zielgerätemodell der Farbraum zugeordnete Farben übergeben werden. Sie verrechnen alle zugeordneten Werte durch das Gegenteil des Offsets, der zuvor auf die neutrale Zielachse angewendet wurde. Dadurch wird die neutrale Zielachse dem ursprünglich vom CAM dargestellten Wert zugeordnet. Gleiches gilt für die Gamutgrenze und alle Zwischenwerte.
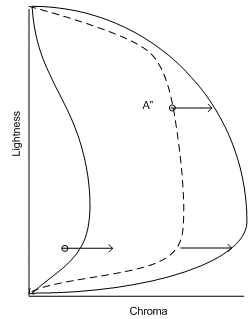
Abbildung 2 : Rückgängigmachen der Ausrichtung der neutralen Zielachse des Geräts
Minimaler Farbunterschied (MinCD)
Minimale Farbdifferenz (MinCD) Relative und absolute Versionen – entspricht der farbmetrischen Absicht von ICC.
Hinweis
Das MinCD GMM eignet sich für die Abbildung von Grafiken und Liniengrafiken mit "Logo"-Farben (Sonderfarben), Logofarbverläufen mit einigen Farben außerhalb des Farbraums und für die letzte Phase der Korrekturtransformationen. Während die MinCD GMM für fotografische Bilder verwendet werden könnte, die sich vollständig innerhalb des Zielbereichs befinden, wird es nicht für das allgemeine Rendern fotografischer Bilder empfohlen. Die Zuordnung von Farben außerhalb des Farbraums zu Farben auf der Zielraumoberfläche kann zu unerwünschten Artefakten führen, z. B. Ton- oder Chromaunregelmäßigkeiten in glatten Farbverläufen, die die Gamutgrenze überschreiten. BasicPhoto wird für fotografische Bilder empfohlen. Wenn ein fotografisches oder kontones Bild eine andere Gamutzuordnung als BasicPhoto erfordert, sollte die Alternative darin bestehen, ein Plug-In-GMM zu erstellen, das diese Zuordnung implementiert, anstatt MinCD zu verwenden.
Die Farbskala bleibt unverändert. Bei Farben außerhalb des Farbraums werden Helligkeit und Chroma angepasst, indem der Punkt im Zielraum gefunden wird, der den Mindestfarbabstand von Eingabepunkten außerhalb des Farbraums aufweist. Der Farbabstand wird im JCh-Bereich berechnet. Sie gewichten jedoch den Abstand in Leichtigkeit (J) und den Abstand in Chroma (C) oder Farbton (h) unterschiedlich. Eine chromaabhängige Gewichtsfunktion wird für die Entfernung in der Leichtigkeit verwendet, sodass das Gewicht für kleine Chroma kleiner und größer für große Chroma ist, bis ein Schwellenwertchromat erreicht ist, nach dem das Gewicht bei 1 bleibt, d. h. das gleiche Gewicht wie die Entfernung in Chroma oder Farbton. Dies folgt der empfohlenen Verwendung für CMC und CIEDE2000. Es gibt zwei Varianten: Relative Farbmetrik und absolute Farbmetrik.
Relative Farbmetrik: Richten Sie zunächst die neutrale Quell- und Zielachse aus, wie zuvor beschrieben. Schneiden Sie dann die angepasste Quellfarbe an die angepasste Zielraumgrenze ab. (Siehe Abbildung 4. Chromazuordnung entlang konstanter Leichtigkeit.) Justieren Sie die Zielgerätewerte wie zuvor beschrieben neu. Im Fall einer monochromen Zielraumgrenze bedeutet die Chromabeschneidung, dass der Chromawert (C) auf 0,0 (0,0) festgelegt ist.
Absolute Farbmetrik: Dies ähnelt der relativen Farbmetrik, jedoch ohne die Ausrichtung der neutralen Quell- und Zielachse. Der Quellwert wird direkt an die neutrale Zielachse gekappt. Beachten Sie, dass das Verhalten mit der relativen farbmetrischen Variante identisch ist, wenn sowohl die Quell- als auch die Zielraumgrenzen monochrom sind. Das heißt, die Ausrichtung der neutralen Achsen wird ausgeführt, und dann wird die Chroma auf 0 geschnitten. Dadurch wird sichergestellt, dass eine angemessene Ausgabe erreicht wird, auch wenn sich die Medien und Farbstoffe erheblich unterscheiden.
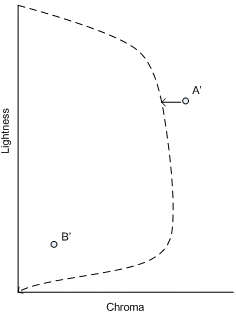
Abbildung 3 : MinCD-Clipping auf den angepassten Gamut
BasicPhoto
Übersicht
BasicPhoto – entspricht der bevorzugten ICC-, Bild- oder Wahrnehmungsabsicht.
Dieser Algorithmus ist eine Variante der chromaabhängigen sigmoidalen Leichtigkeitszuordnung und cusp Knee Scaling (SGCK), die von CIE TC8-03 in CIE156:2004 beschrieben wird. Dieser Variantenalgorithmus unterstützt GAMUT-Begrenzungsdeskriptoren (GBDs) mit Shells mit doppeltem Gamut; d. h. GBDs mit einer Referenzshell und einer plausiblen Shell. Der SGCK-Algorithmus, der ursprünglich nur eine Gamut-Shell in der GBD annimmt, basiert auf dem SIG_KNEE Algorithmus (Braun 1999), der die sigmoidale Leichtigkeitszuordnung und die Von Braun und Fairchild (1999) vorgeschlagene Skalierung der Kniefunktion enthält, kombiniert mit der Chromaabhängigkeit von GCUSP (Morovic, 1998). Es hält den wahrgenommenen Farbton konstant, z. B. den Farbtonwinkel in farbkorrekturer Jab, und verwendet eine generische (bildunabhängige) sigmoidale Helligkeitsskalierung, die chromaabhängig und eine 90-prozentige Kniefunktionschromatie angewendet wird. Die Variante skaliert mit konstanter Leichtigkeit.
Der Fall einer Shell mit einem einzelnen Gamut
Es ist hilfreich, den Algorithmus zu überprüfen, wenn sowohl Quell- als auch Ziel-GBDs nur eine Gamutshell aufweisen. In diesem Fall besteht der Algorithmus aus den folgenden Berechnungen.
Führen Sie zunächst die erste Leichtigkeitszuordnung mithilfe der folgenden Formel aus:
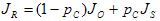 (1)
(1)
wobei Jₒ die ursprüngliche Leichtigkeit und JR die Reproduktionsleichtigkeit ist.
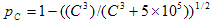 (2)
(2)
Wenn die Quellraumgrenze monochrom ist, ist der Chromawert für die monochrome Begrenzung aufgrund der Ausrichtung der neutralen Achse null. Dies führt zu dem degeneraten Fall, in dem C gleich 0 ist. In diesem Fall ist pC auf 1 festgelegt.
pC ist ein chromaabhängiger Gewichtungsfaktor (Morovic, 1998), der von der Chroma der ursprünglichen Farbe abhängt, C und JS sind das Ergebnis der ursprünglichen Leichtigkeit, die mithilfe einer sigmoidalen Funktion zugeordnet wird.
Zur Berechnung von JS (Braun und Fairchild, 1999) wird zunächst eine eindimensionale Nachschlagetabelle (LUT) zwischen Original- und Reproduktionsleichtheitswerten auf Der Grundlage einer diskreten kumulativen Normalfunktion (S) eingerichtet.
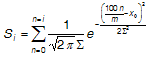 (3)
(3)
wobei x ₀ und S die Mittel- und Standardabweichung der Normalverteilung bzw. i = 0,1,2... m,m ist die Anzahl der in der LUT verwendeten Punkte. Si ist der Wert der kumulativen Normalfunktion für i /m Prozent. Die Parameter hängen von der Leichtigkeit des schwarzen Punkts der Reproduktionsskala ab und können aus Tabelle 1 interpoliert werden. Einzelheiten zur Berechnung dieser Parameter finden Sie unter Braun und Fairchild (1999, S. 391).
J minOut
5.0
10.0
15.0
20.0
x ₀
53.7
56.8
58.2
60.6
E
43.0
40.0
35.0
34,5
Tabelle 1 : BasicPhoto-Lightness-Komprimierungsparameterberechnung
Um S als Lightness Mapping LUT (S LUT ) zu verwenden, muss es zuerst in den Helligkeitsbereich von [0,100] normalisiert werden. Die normalisierten Daten werden dann in den dynamischen Bereich des Zielgeräts skaliert, wie in Formel 4 gezeigt, wobei Jmin\ Out und Jmax\ Out die Werte der Helligkeit des schwarzen Punkts bzw. des Weißpunkts des Reproduktionsmediums sind.
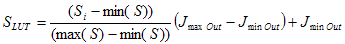 (4)
(4)
An diesem Punkt können die J S-Werte aus der S-LUT abgerufen werden, indem zwischen den m-Punkten der entsprechenden J O' - und J S-Werte interpoliert wird und die folgende Gleichung als Eingabe verwendet wird.
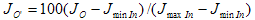 (5)
(5)
J minIn ist der Helligkeitswert des schwarzen Punkts des ursprünglichen Mediums, J maxIn ist der Helligkeitswert des Weißpunkts des ursprünglichen Mediums, und J O ist die ursprüngliche Leichtigkeit. Für einen späteren Verweis können Sie von S die sigmoidale Funktion bezeichnen, die in der soeben beschriebenen Weise definiert ist, wie in der folgenden Abbildung 4 dargestellt.
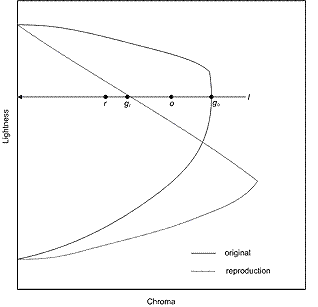
Abbildung 4 : Chromazuordnung mit konstanter Leichtigkeit
Zweitens, wenn die Zielraumgrenze chromatisch ist, komprimieren Sie Chroma entlang linien konstanter Leichtigkeit (l), und führen Sie die Komprimierung wie folgt aus.
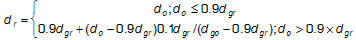 (6)
(6)
wobei d die Entfernung von E auf l darstellt; g stellt die Mittlere Gamutgrenze dar; r stellt die Reproduktion dar; und o die ursprüngliche Abbildung 5.
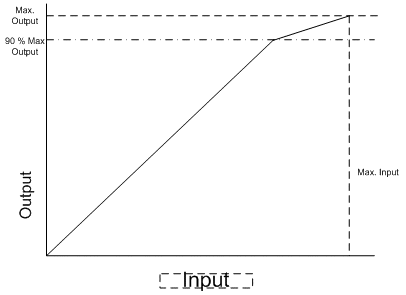
Abbildung 5 : Komprimierung von Chroma und Leichtigkeit in BasicPhoto
Wenn die Zielraumgrenze monochrom ist, wird der Chromawert auf 0 abgeschnitten.
Drittens: Verwenden Sie einen MinCD-Clip (weiter oben beschrieben), um restfehler zu beseitigen.
Schwarz-Erweiterung
Der vorherige Algorithmus kann geändert werden, um die Schwarz zu verbessern, wenn das Ziel ein Druckergerät ist. Das Problem hat mit der Wahl von JminOut zu tun, die in der Regel nicht der dunkelsten Farbe entspricht, die ein Drucker erzeugen kann.
Genauer gesagt ist die Farbe mit der höchsten Dichte, die durch Das Platzieren von 100 Prozent Tinten (oder die maximale mögliche Abdeckung, wenn GCR/Freihandbegrenzung wirksam ist), normalerweise nicht "neutral" im Farbdarstellungsraum. Siehe Abbildung 6. Mit anderen Worten, wenn neutrale minimale Leichtigkeit für das Zielgerät verwendet wird, wird der erstellte Helligkeitsskalierer einer minimalen Leichtigkeit zugeordnet, die nicht die höchste Dichte ist, die vom Drucker erreicht werden kann. Betrachten Sie den weiteren Anwendungsfall von Monitor zu Drucker. Der Monitor schwarz, R=G=B=0, wird dann als nicht die höchste Dichte gedruckt. Dies wirkt sich auf die Bildqualität aus, da es an Tiefe und Kontrast mangelt.
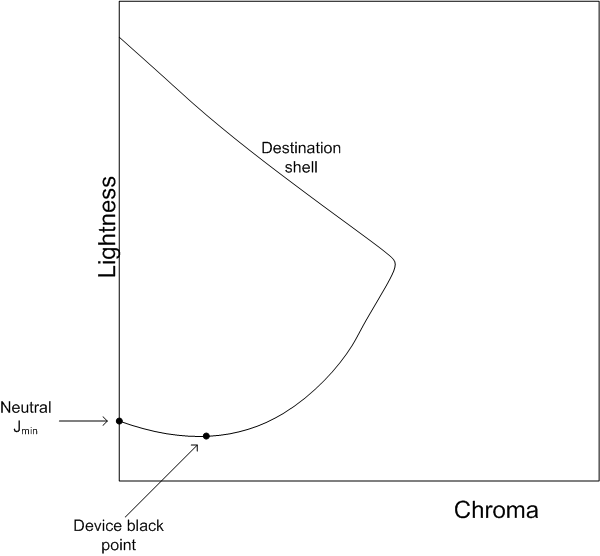
Abbildung 6 : Der schwarze Punkt des Geräts kann dunkler sein als die neutrale Minimale Helligkeit.
Angenommen, das Ziel "Schwarzer Punkt des Geräts" ist Jkakbk/JkCkh k. Wenn C k nicht 0 ist, ist der schwarze Punkt des Geräts im Verhältnis zu CAM02 nicht neutral. Wenn Sie J k für das Ziel "neutrale minimale Leichtigkeit" bei der Konstruktion des Lightness Scalers verwenden; d.a. Festlegen
JminOut = Jk
und wenden Sie sie auf die Quellraumshell an, und Sie erhalten die in Abbildung 7 dargestellte Konfiguration. In der Abbildung entspricht die Farbtonebene h k.

Abbildung 7 : Geometrie unter Verwendung der geänderten Helligkeitsskala mit schwarzem Punkt des Zielgeräts
Damit der nachfolgende Chromakomprimierungsalgorithmus fortfahren kann, möchten Sie die maximale und minimale Helligkeit an den Quell- und Zielshells ausrichten. Dies kann erreicht werden, indem die Zielshell zwischen J neutralMin und J k durch Verschieben von Punkten nach links angepasst wird. Darüber hinaus muss diese Transformation auf den gesamten Jab-Raum angewendet werden, nicht nur auf die Farbtonebene, die h k entspricht.
Die Transformation ist
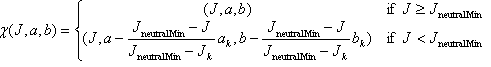
Abbildung 8 zeigt die Auswirkungen der Transformation.
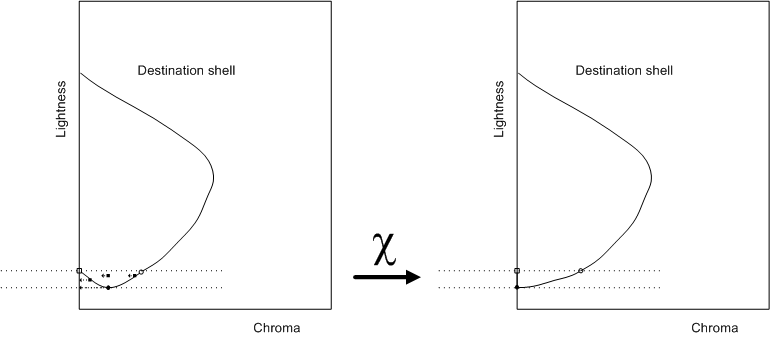
Abbildung 8 : Geometrie unter Verwendung der geänderten Helligkeitsskala mit schwarzem Punkt des Zielgeräts
Nach dem Anwenden des üblichen Chromakomprimierungsalgorithmus muss der Punkt "zurückversetzt" werden, d. h. die umgekehrte Transformation muss angewendet werden, um die endgültige zugeordnete Farbe zu erhalten.
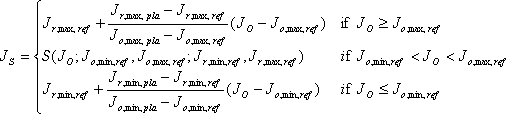
Der Fall von Shells mit doppeltem Gamut
Das Ziel besteht darin, SIG_KNEE für die Shell mit einem einzelnen Farbraum auf den Fall zu verallgemeinern, in dem entweder die GBD des Quellgeräts oder das Zielgerät GBD eine Zwei-Shell-Struktur aufweist. Die innere Shell wird als Referenzshell bezeichnet, während die äußere Shell als Plausible Shell bezeichnet wird. Sie möchten die folgenden Fälle berücksichtigen.
(a) Sowohl das Quell-GBD als auch das Ziel-GBD verfügen über eine Zwei-Shell-Struktur.
(b) Die Quell-GBD verfügt über eine Zwei-Shell-Struktur; die Ziel-GBD verfügt nur über eine Shell.
(c) Die Quell-GBD verfügt nur über eine Shell; die Ziel-GBD verfügt über eine Zwei-Shell-Struktur.
(d) Sowohl das Quell-GBD als auch das Ziel-GBD verfügen nur über eine Shell.
Fall (d) ist der Fall der Shell mit einem einzelnen Bereich, der zuvor erläutert wurde. Für Die Fälle (a), (b) und (c) können Sie die Neuskalierung der Leichtigkeit generalisieren, um die zusätzlichen Informationen aus der Dual-Shell-Struktur zu verwenden. In Den Fällen (b) und (c), in denen entweder die Quelle oder das Ziel nur über eine Shell verfügt, führen Sie eine "induzierte Verweisshell" ein, die in einem nachfolgenden Abschnitt erläutert wird, "Induzierte Referenzshell". Der allgemeine Algorithmus für zwei Shells wird für die Groß-/Kleinschreibung (a) beschrieben. Nachdem die Induced Reference Shell-Konstruktion erläutert wurde, kann der Algorithmus auch auf die Groß- und Kleinschreibung (b) und (c) angewendet werden. Bei der Chromakomprimierung wird das Komprimierungsverhältnis von den größten verfügbaren Shells bestimmt. Mit anderen Worten, wenn sowohl die Plausible Shell als auch die Referenzshell verfügbar sind, wird die Plausible Shell verwendet. Andernfalls wird die Referenzshell verwendet.
Generalisierte Neuskalierung der Helligkeit
Das Vorhandensein von zwei Shells für Quell- und Ziel-GBD bedeutet, dass Sie einen Satz von vier Punkten aus der Quell-GBD einem entsprechenden Satz in der Ziel-GBD zuordnen müssen.
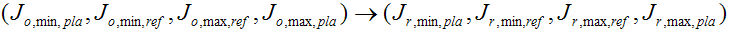
Die Tiefschreibungen haben die folgende Bedeutung.
o oder r: "Original" (Quelle) oder "Reproduktion" (Ziel)
min oder max: minimale neutrale Oder maximale neutrale Leichtigkeit
pla oder ref: Plausible Shell oder Reference Shell
Die Reihenfolge in jedem Vierfach ist auch die erwartete relative Größe dieser Punkte.
Die Karte der Neuskalierung der Helligkeit verwendet dieselben beiden Formeln wie die einzelne Shell, aber J S wird stückweise wie folgt definiert.
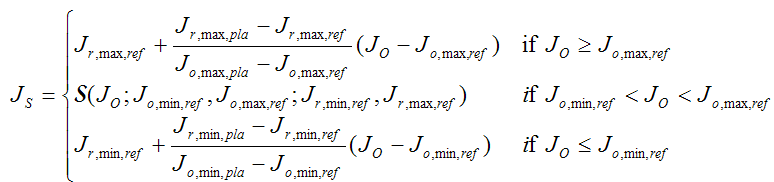 (7)
(7)
Mit anderen Worten, es ist sigmoidal innerhalb der Referenzshell und linear außerhalb. Weitere Informationen in Abbildung 9.
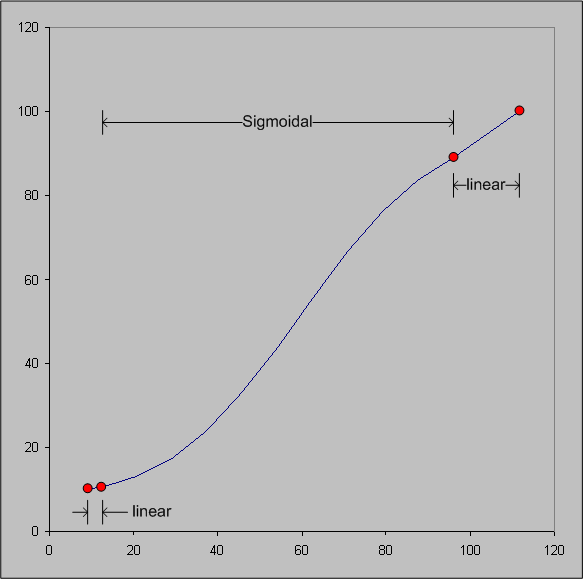
Abbildung 9 : Funktion zur Neuskalierung der Leichtigkeit für GBDs mit zwei Shells
INDUZIERTE REFERENZSHELL
Wenn eine GBD über eine Shell und die andere GBD über zwei Shells verfügt, müssen Sie eine "Referenzshell" für die GBD mit nur einer Shell erstellen. Die vorhandene Shell, die als Verweisshell bezeichnet wird, wird in "Plausible Shell" geändert. Tatsächlich müssen Sie keine Shell im vollen Jab-Bereich erstellen. Da bei der Neuskalierung der Helligkeit nur J max und J min verwendet werden, müssen Sie diese Werte nur für die induzierte Verweisshell nachholen. Es gibt zwei Fälle, je nachdem, welche GBD über zwei Shells verfügt.
Fall 1: Quell-GBD verfügt über zwei Shells; Ziel-GBD verfügt über eine Shell.
Bestimmen Sie die zielinduzierte Referenzshell auf der neutralen Achse. d. h. die J r,\ min,\ ref und J r,\ max,\ ref der Shell. Dazu wird der folgende Algorithmus verwendet.
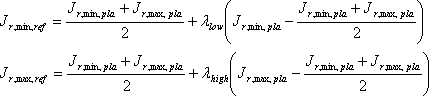
Die Faktoren ? niedrig und ? hohe Kontrolle der Trennung zwischen der Plausible Shell und der Referenzshell. Ein Wert von 1 bedeutet, dass die J-min-Werte oder J mₐₓ-Werte übereinstimmen. Ihre Werte werden von der Quellreferenzshell und der Plausiblen Quellshell "induziert".
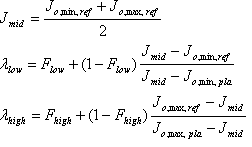
Die "Fudge-Faktoren" F niedrig und F hoch sind abstimmbare Parameter , die zwischen 0 und 1 liegen müssen. Wenn der Wert 0 ist, werden die J min oder J mₐₓ direkt von den Quellshells induziert. Wählen Sie in diesem Fall F low = 0,95 und F high = 0,1 aus.
Fall 2: Quell-GBD verfügt über eine Shell; Destination GBD verfügt über zwei Shells.
Bestimmen Sie die quellinduzierte Verweisshell auf der neutralen Achse. Das heißt, J o,\ min,\ ref und J o,\ max,\ ref der Shell. Dazu wird der folgende Algorithmus verwendet.
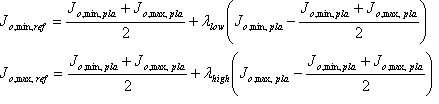
Wieder die Faktoren ? low und ? hohe Kontrolle über die Trennung zwischen der Plausiblen Shell und der Referenzshell. Ein Wert von 1 bedeutet, dass die J-min-Werte oder J mₐₓ-Werte übereinstimmen. Ihre Werte werden von der Quellreferenzshell und der Plausiblen Quellshell "induziert":
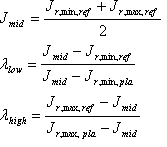
Gründe für Änderungen gegenüber den Empfehlungen des CIE TC8-03
BasicPhoto unterscheidet sich von den Empfehlungen von CIE TC8-03 in den folgenden Punkten.
- Chroma wird nicht in Richtung des Keils komprimiert, sondern entlang von Linien konstanter Leichtigkeit.
- Der Helligkeitsbereich verwendet die Helligkeit der dunkelsten Farbe im Gamut und nicht den Punkt, an dem die Gamutgrenze die neutrale Achse überschreitet.
- BasicPhoto unterstützt sowohl eine Referenz-Gamut-Shell als auch eine plausible Gamut-Shell, wenn eine gamut-Grenze in der Transformation über zwei Shells verfügt.
- BasicPhoto verwendet CIECAM02; anstatt CIECAM97s zu verwenden, um bei 400 cd/m2 in D65 zu konvertieren, und dann den RIT IPT-Farbraum zu verwenden.
Die erste Änderung wurde vorgenommen, um Toninversionsprobleme zu verhindern, die auftreten können, wenn die Komprimierung zu einem Cusp verwendet wird. Wie in Abbildung 10 gezeigt, kann die Cusp-Komprimierung zu Toninversionen führen. Dies kann passieren, wenn Farben mit hohem Chroma heller sind als Farben mit niedrigerem Chroma. Da SGCK jedes Pixel unabhängig voneinander in Helligkeit und Chroma komprimiert, ist es nicht garantiert, dass die Helligkeitsbeziehung zwischen den Pixelwerten nach der Komprimierung beibehalten wird. Der bekannte Nachteil dieser Entscheidung, auf Linien von konstanter Leichtigkeit zu komprimieren, ist, dass Sie Verluste von Chroma erleiden können, insbesondere in Bereichen, in denen die Ziel gamut Grenze sehr flach ist, wie es bei hellen Gelben der Fall ist.
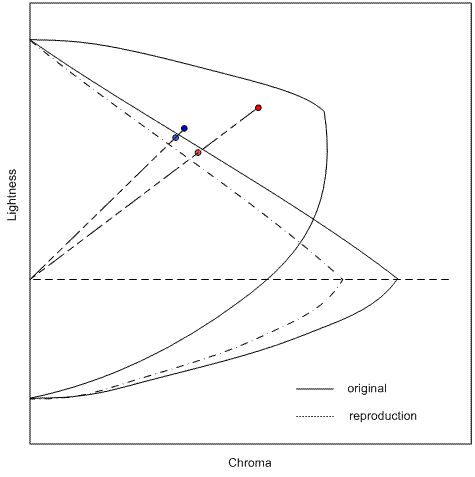
Abbildung 10 : Durch SGCK verursachte Toninversion



Abbildung 11 : Originalbild, SGCK-Ergebnis und BasicPhoto-Ergebnis
Abbildung 11 veranschaulicht diese Tonumkehrung. Auf der linken Seite befindet sich ein Originalbild, das von einer Digitalkamera aufgenommen wurde; in der Mitte das Bild, wie von SGCK reproduziert; und auf der rechten Seite das Bild, wie von BasicPhoto reproduziert. Das Bild auf der linken Seite befindet sich im Farbraum der Digitalkamera, die Mitte und rechte Bilder befinden sich im Farbraum eines LCD-Videodisplays. Im Originalbild ist der obere Teil der Teekanne dunkler als der untere, da der Boden die Tischdecke widerspiegelt, auf der sie sitzt. Im SGCK-Bild ist der obere Teil aufgrund der Toninversion tatsächlich heller als der untere. Außerdem ist es schwierig, die Elemente im unteren Teil der Teekanne zu sehen. Auf der rechten Seite hat BasicPhoto die Ton-Inversion behoben und die reflektierten Artikel sind deutlicher zu unterscheiden.
Die zweite Änderung wurde vorgenommen, um die Wiedergabe nahezu schwarzer Farben auf Druckern zu verbessern, bei denen das schwärzlichste Schwarz nicht direkt auf die neutrale CIECAM02-Achse fällt. Die folgende Abbildung 12 zeigt ein Bild, das in sRGB konvertiert wurde; reproduziert für einen RGB-Tintenstrahldrucker mit SGCK; und reproduziert für denselben Drucker mit BasicPhoto. Das Bild in der Mitte verwendet nicht das gesamte Gerät schwarz, und daher fehlt der Kontrast im Original. Der Kontrast wird mit BasicPhoto wiederhergestellt.



Abbildung 12 : Erweitertes Schwarz
Die dritte Änderung wurde vorgenommen, um die Farbwiedergabe für Digitalkameras zu verbessern. Insbesondere in Fällen, in denen die Digitalkamera mithilfe eines Referenzziels profiliert wurde, enthält eine aus gemessenen Farben erstellte Beschreibung der Gamutgrenze möglicherweise nicht alle Farben, die in einer realen Szene erfasst werden. Anstatt alle Farben auf den Farbumfang des gemessenen Farbziels zu schneiden, lassen Sie die Extrapolation zu, um eine plausible Gamutgrenze zu erzeugen. Der BasicPhoto-Algorithmus wurde entwickelt, um eine solche extrapolierte Gamutgrenze zu unterstützen.
Die vierte Änderung wurde vorgenommen, da CIECAM02 gut für die Gamutzuordnung geeignet ist. Der von TC8-03 empfohlene Prozess der Konvertierung von Gerätefarben in D65 bei 400 cd/m2 und der anschließenden Verwendung des RIT IPT-Farbraums ist sowohl rechenintensiv als auch zeitaufwändig.
Farbtonzuordnung
HueMap entspricht der Absicht ICC Saturation.
Wenn entweder die Quell gamut-Grenze oder die Zielbereichsgrenze keine Primärwerte enthält, wird für dieses Modell das in einem vorherigen Abschnitt beschriebene MinCD-Modell (relativ) verwendet. beispielsweise Geräte, für die die Primaries nicht bestimmt werden können (ICC-Profile mit mehr als vier Kanälen) oder monochrome ICC-Profile.
Dieser Algorithmus passt zuerst den Farbton des Eingabefarbwerts an. Anschließend wird gleichzeitig die Helligkeit und das Chroma mithilfe einer Scherungszuordnung angepasst. Schließlich schneidet er den Farbwert ab, um sicherzustellen, dass er sich innerhalb des Farbumfangs befindet.
Der erste Schritt besteht darin, die "Hue Wheels" zu bestimmen. Suchen Sie die JCh-Werte für primäre und sekundäre Farben für quell- und zielgerät. Sie berücksichtigen nur die Farbtonkomponenten. Dies führt zu einem primären oder sekundären Farbrad mit sechs Farbpunkten für jedes Gerät. (Siehe Abbildung 13.)
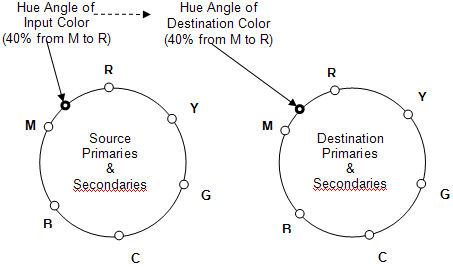
Abbildung 13 : Hue-Räder
Bessere Ergebnisse können erzielt werden, wenn die blaue primäre Quelle nicht zum primären Zielblau gedreht wird. Stattdessen wird der primäre Farbtonwinkel der Quelle blau als primärer Farbtonwinkel des Zielblaus verwendet.
Führen Sie als Nächstes die Farbtondrehungen für jede Eingabefarbe aus dem Quellbild aus.
a)Bestimmen Sie mithilfe des Farbwinkels der Eingabefarbe die Position der Farbe im Quellfarbrad relativ zu den beiden benachbarten Primär- oder Sekundärfarben. Die Position kann als Prozentsatz des Abstands zwischen den Primaren betrachtet werden. Beispielsweise beträgt der Eingabefarbton 40 Prozent des Weges vom Farbtonwert von Magenta zum Farbtonwert von Rot.
b)Suchen Sie auf dem Zielfarbrad den zugeordneten Farbtonwinkel, z. B. 40 Prozent von Magenta zu Rot. Dieser Wert ist der Zieltonwinkel.
Im Allgemeinen werden die Ausgangs- und sekundären Quellen nicht denselben Farbtonwinkel aufweisen wie die Zielprimien und Sekundäre; Das heißt, der Zieltonwinkel unterscheidet sich in der Regel vom Quellfarbwinkel.
Angenommen, die Farbtonräder erzeugen die folgenden Werte:
Quelle M = 295 Grad, Quelle R = 355 Grad.
Ziel M = 290 Grad, Ziel R = 346 Grad.
Wenn der Farbtonwinkel der Eingabefarbe 319 Grad beträgt, beträgt er 40 Prozent des Winkels (24 Grad) von Quelle M bis Quelle R. Der Winkel von M bis R beträgt 60 Grad, und der Winkel von M zum Eingabeton beträgt 24 Grad. Berechnen Sie den Winkel auf dem Ziel, der 40 Prozent zwischen Ziel M und Ziel R (22 Grad) beträgt, sodass der Farbtonwinkel der Zielfarbe 312 Grad beträgt.
Als Nächstes berechnen Sie die Farbtonreferenzpunkte für den Quellton und den Zielton. Um den Farbtonbezugspunkt für einen bestimmten h -Wert (Farbton) zu berechnen, möchten Sie den Wert J (Helligkeit) und C (Chroma) ermitteln.
- Ermitteln Sie den J-Wert des Farbtonbezugspunkts, indem Sie zwischen den J-Werten für die benachbarten primären oder sekundären Punkte interpolieren, wobei die relative Position des Farbtons verwendet wird. beispielsweise 40 Prozent in diesem Beispiel.
- Suchen Sie den maximalen C-Wert bei diesem J-Wert und h-Wert. Sie verfügen jetzt über den JCh des Farbtonreferenzpunkts für diesen Farbton.
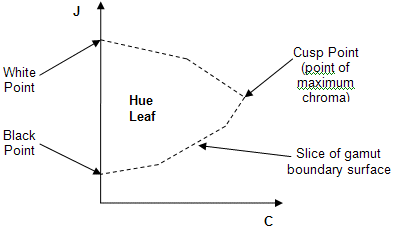
Abbildung 14 : Ein Farbtonblatt (Visualisierung einer Gamutgrenze bei einem bestimmten Farbton)
Der nächste Schritt besteht darin, die Scherzuordnung für jedes Pixel zu berechnen. Visualisieren Sie zunächst ein Farbtonblatt aus dem Quell gamut für den Farbtonwinkel der Quellfarbe und ein Farbtonblatt aus dem Zielumfang für den Zieltonwinkel, der während der Farbtonrotation berechnet wird. Die Farbtonblätter werden erstellt, indem ein "Slice" von der JCh-Gamutgrenze in einem bestimmten Farbtonwinkel genommen wird (siehe Abbildung 14).
HINWEIS: Aus Gründen der Leistungsoptimierung werden Farbtonblätter nicht tatsächlich erstellt. sie werden hier nur zu Visualisierungszwecken beschrieben und angezeigt. Die Vorgänge werden direkt auf der Gamutgrenze im angegebenen Farbton ausgeführt. Anschließend berechnen Sie die Farbtonreferenzpunkte, um die Scherzuordnung zu bestimmen.
- Führen Sie eine Helligkeitsänderung durch, um die Schwarzweißpunkte des Quellblatts dem Zielblatt zuzuordnen (siehe Abbildung 15). Die schwarzweißen Punkte des Quelltonblatts werden linear den schwarzweißen Punkten des Zieltonblatts zugeordnet, indem alle J-Koordinaten der Quellgrenze skaliert werden. Der farblich zugeordnete Eingabefarbwert wird auf die gleiche Weise skaliert.
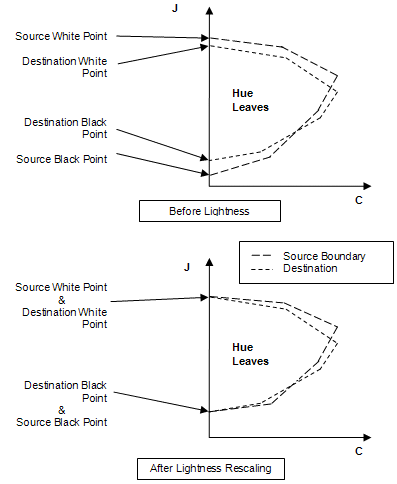
Abbildung 15 : Zuordnung der Leichtigkeit
- Bestimmen Sie die Farbtonreferenzpunkte für jedes Farbtonblatt. Wenden Sie eine Scherzuordnung auf das Quellblatt an, damit quell- und zielverweispunkte übereinstimmen (siehe Abbildung 16). Der Bezugspunkt für einen Gamut bei einem bestimmten Farbton ist der interpolierte Farbtonbezugspunkt zwischen den angrenzenden Primaren. Der Bezugspunkt des Quelltonblatts wird linear dem Bezugspunkt des Zieltonblatts zugeordnet, wobei ein "Schervorgang" verwendet wird, der die J-Achse sperrt und die schwarzen und weißen Punkte stationär hält. Die schwarzen Punkte, weißen Punkte und Bezugspunkte der Quell- und Zieltonblätter sollten übereinstimmen.
- Wenden Sie die Scherzuordnung auf den Wert der eingabebereinigten Eingabefarbe an. Die J- und C-Koordinaten des Quellfarbwerts werden proportional skaliert, relativ zum Abstand von der J-Achse.
- Als Nächstes wird eine subtile chromaabhängige Helligkeitskomprimierung in Richtung des J-Werts des Farbbezugspunkts für den scherenden Farbpunkt durchgeführt. Die Komprimierung zum Farbtonbezug J erfolgt gammaartig, wobei Weiß, Schwarz, Grau und Punkte auf der Farbtonreferenz J nicht betroffen sind. Alle anderen Punkte neigen auf glatte Weise zum Farbtonbezug J, leicht in der Nähe der Farbtonreferenz J, wobei der Farbton konstant bleibt. Die Chroma-Abhängigkeit stellt sicher, dass neutrale Farben nicht beeinflusst werden, und der Effekt wird bei Farben mit höherem Chroma erhöht.
Im Folgenden finden Sie eine mathematische Beschreibung der Helligkeitskomprimierung in Richtung des Farbtonbezugs J oder der Anpassung des J-Werts des Zielpunkts. Er wird als Zielpunkt bezeichnet, da er der Zielskala zugeordnet wurde.
Berechnen Sie zunächst "factorC" (Chroma-Abhängigkeitsfaktor) für den Zielpunkt, der bestimmt, wie viel Wirkung die Helligkeitskomprimierung haben wird. Punkte in der Nähe oder auf der J-Achse weisen nur eine geringe oder keine Komprimierung auf; Für Punkte, die weiter von der J-Achse entfernt sind (high-chroma), wird mehr Komprimierung angewendet. Multiplizieren Sie mit 0,5, um sicherzustellen, dass factorC kleiner als 1 ist, da sourceC möglicherweise etwas größer als referenceC, aber nicht doppelt so groß sein kann.
factorC = (destinationC / referenceC) ? 0.5
Dabei gilt Folgendes:
destinationC ist der C-Wert des Zielpunkts.
referenceC ist der C-Wert des Hue-Referenzpunkts.
Ermitteln Sie als Nächstes, ob der Zielpunkt J oberhalb oder unterhalb des Farbtonbezugs J liegt. Gehen Sie wie folgt vor:
Berechnen Sie "factorJ" für den Zielpunkt relativ zum VerweisJ. Dieser FactorJ-Wert liegt zwischen 0 und 1 (0 bei referenceJ; 1 bei maxJ).
factorJ = (destinationJ - referenceJ) / (maxJ - referenceJ)
Dabei gilt Folgendes:
destinationJ ist der J-Wert des Zielpunkts.
referenceJ ist der J-Wert des Farbtonbezugspunkts.
maxJ ist der maximale J-Wert des Gamuts.
Wenden Sie eine Gamma-ähnliche Leistungsfunktion auf factorJ an, wodurch factorJ um einen bestimmten Betrag reduziert wird. In diesem Beispiel wird die Stärke 2 (das Quadrat) verwendet. Subtrahieren Sie den reduzierten FaktorJ vom ursprünglichen FaktorJ, und multiplizieren Sie das Ergebnis mit dem gesamten J-Bereich über dem primären VerweisJ, um die "deltaJ" zu finden, die die Änderung in J nach der Helligkeitskomprimierung darstellt, jedoch nicht die Chromaabhängigkeit.
deltaJ = (factorJ - (factorJ ? factorJ)) ? (maxJ – referenceJ)
Wenden Sie factorC auf deltaJ an (je höher die Chroma, desto größer der Effekt), und berechnen Sie den neuen J-Wert für den Zielpunkt.
destinationJ = destinationJ - (deltaJ ? factorC)
Wenn der J-Wert für den Zielpunkt unterhalb von referenceJ liegt, wird eine ähnliche Berechnung wie die vorherigen Schritte A-C ausgeführt, wobei minJ anstelle von maxJ verwendet wird, um den Bereich in J zu ermitteln, um den FaktorJ zu berechnen, und unter Berücksichtigung der Polarität der Vorgänge "unterhalb" des ReferenceJ.
factorJ = (referenceJ - destinationJ) / (referenceJ - minJ)
deltaJ = (factorJ - (factorJ ? factorJ)) ? (referenceJ – minJ)
destinationJ = destinationJ + (deltaJ ? factorC)
Dabei gilt Folgendes:
minJ ist der minimale J-Wert des Gamuts.
Das Chroma für Eingabefarbpunkte wird linear (wenn möglich) entlang einer konstanten Helligkeit erweitert, die proportional zum maximalen Chromawert des Quell- und Zielbereichs bei diesem Farbton und dieser Helligkeit ist. In Kombination mit der vorangehenden chromaabhängigen Helligkeitskomprimierung trägt dies dazu bei, die Sättigung zu erhalten, da die Scherungszuordnung mithilfe der Referenzpunkte manchmal dazu führt, dass der Quellpunkt in Chroma überkomprimieren wird (siehe Abbildung 16).
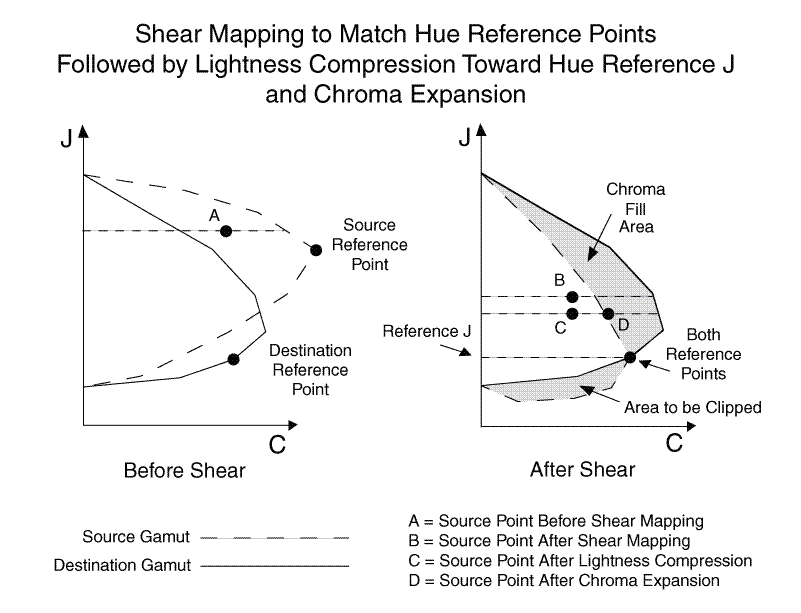
Abbildung 16 : Scherenzuordnung, Helligkeitskomprimierung in Richtung Farbtonbezug J und Chroma-Erweiterung
Es folgt eine mathematische Beschreibung des Chroma-Expansionsprozesses oder der Anpassung des C-Werts des Zielpunkts. Er wird als Zielpunkt bezeichnet, da er scherend zugeordnet wurde und die Helligkeit in die Zielskala komprimiert wurde.
Bestimmen Sie vor der Scherungszuordnung sourceExtentC (die Chromaausdehnung an der Helligkeit und dem Farbton des Quellpunkts).
Bestimmen Sie nach der Scherungszuordnung und der Helligkeitskomprimierung, die den Quellpunkt in den Zielpunkt transformiert, den destExtentC (die Chromaausdehnung an der Helligkeit und dem Farbton des Zielpunkts).
Wenn sourceExtentC größer als der destExtentC ist, ist keine Chromaanpassung am Zielpunkt erforderlich, und Sie können den nächsten Schritt überspringen.
Passen Sie destinationC (die Chroma des Zielpunkts) so an, dass sie bei dieser Helligkeit und diesem Farbton in die Ziel-Chroma-Ausdehnung passt.
destinationC = destinationC ? (destExtentC / sourceExtentC)
Dabei gilt Folgendes:
destinationC ist der C-Wert des Zielpunkts.
sourceExtentC ist der maximale C-Wert des Quellumfangs bei der Helligkeit und dem Farbton des Quellpunkts.
destExtentC ist der maximale C-Wert des Zielumfangs bei der Helligkeit und dem Farbton des Zielpunkts.
Führen Sie schließlich den Mimimumabstandsausschnitt aus. Wenn die Farbton-, Helligkeitsanpassungs- und Scherschnitteingabefarbe immer noch etwas außerhalb des Zielbereichs liegt, schneiden Sie sie an den nächstgelegenen Punkt an der Zielbereichsgrenze ab (siehe Abbildung 17).
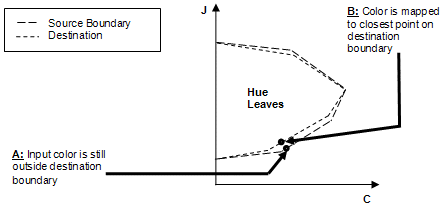
Abbildung 17 : Mindestabstandsausschnitt
Gamut Boundary Description and Gamut Shell Algorithmen
Die Geräte gamut boundary-Funktion verwendet die Gerätemodell-Engine und analytische Parameter, um eine Farbgeräte-Gamutgrenze abzuleiten, die als indizierte Vertexliste des Rumpfs des Geräteumfangs beschrieben wird. Der Rumpf wird unterschiedlich berechnet, je nachdem, ob Sie mit additiven Geräten wie Monitoren und Projektoren oder mit subtraktiven Geräten arbeiten. Die indizierte Scheitelpunktliste wird in CIEJab gespeichert. Die Struktur der indizierten Vertexliste ist für die Hardwarebeschleunigung durch DirectX optimiert.
Dieser Ansatz verfügt über viele bekannte Lösungen. Wenn Sie im Web nach "konvex hull DirectX" suchen, erhalten Sie mehr als 100 Treffer. Beispielsweise gibt es eine Referenz aus dem Jahr 1983 zu diesem spezifischen Thema (Computer Graphics Theory and Application, "Shiphulls, b-spline surfaces, and cadcam," S. 34-49) mit Referenzen aus den Jahren 1970 bis 1982 zum Thema.
Die Sammlung von Punkten kann anhand von extern verfügbaren Informationen wie folgt bestimmt werden:
- Punkte für die Referenzshell für Monitore werden mithilfe einer Stichprobenentnahme des Farbwürfels im Gerätefarbstoffbereich generiert.
- Punkte für die Referenzshell für Drucker und Erfassungsgeräte werden aus den Beispieldaten abgerufen, die zum Initialisieren des Modells verwendet werden.
- Punkte für die Referenzshell für scRGB und sRGB werden mithilfe einer Stichprobenentnahme des Farbwürfels für sRGB generiert.
- Punkte für die plausible Shell für Aufnahmegeräte werden mithilfe einer Stichprobenentnahme des Farbwürfels im Gerätefarbstoffbereich generiert.
- Punkte für die Referenzschale für Projektoren werden mithilfe einer Stichprobenentnahme eines Polyeders im Farbwürfel des Geräts generiert.
- Punkte für die mögliche Shell für große dynamische Farbräume werden mithilfe einer Stichprobenentnahme des Farbwürfels im Raum selbst generiert.
Sie können eine Vertexliste erstellen, die den Farbumfang der Geräte effizient beschreibt, wenn ein Geräteprofil und Systemunterstützungsdienste vorhanden sind.
Bei Ausgabegeräten beschreibt die Gamutgrenze den Farbbereich, der vom Gerät angezeigt werden kann. Aus denselben Daten, die zum Modellieren des Geräteverhaltens verwendet werden, wird eine Gamutgrenze generiert. Konzeptionell geben Sie ein Sampling des Farbbereichs aus, den das Gerät erzeugen kann, messen die Farben, konvertieren die Messungen in einen Darstellungsbereich und verwenden dann die Ergebnisse, um die Gamutgrenze zu erstellen.
Eingabegeräte sind schwieriger. Jedes Pixel in einem Eingabebild muss einen Bestimmten Wert aufweisen. Jedes Pixel muss in der Lage sein, jede Farbe in der realen Welt in irgendeiner Weise darzustellen. In diesem Sinne sind keine Farben für ein Eingabegerät "out of gamut", da sie immer dargestellt werden können.
Alle digitalen Bildformate weisen einen festen dynamischen Bereich auf. Aufgrund dieser Einschränkung gibt es immer einige unterschiedliche Reize, die demselben digitalen Wert zugeordnet sind. Sie können also keine 1:1-Zuordnung zwischen realen Farben und Digitalen Kamerawerten einrichten. Stattdessen wird die Gamutgrenze gebildet, indem ein Bereich von realen Farben geschätzt wird, die die digitalen Antworten der Kamera erzeugen können. Sie verwenden diesen geschätzten Bereich als Gamut für das Eingabegerät.
Grundtypen sind enthalten, um eine Gamutzuordnung für Geschäftsgrafiken bereitzustellen.
Im echten objektorientierten Stil abstrahieren Sie die zugrunde liegende Darstellung der Gamutgrenze. Dies ermöglicht Ihnen die Flexibilität, die Darstellung in Zukunft zu ändern. Um den im neuen CTE verwendeten Gamut Boundary Descriptor (GBD) zu verstehen, müssen Sie zunächst verstehen, wie Gamut Mapping-Algorithmen (GMAs) funktionieren. Traditionell wurden GVO so konzipiert, dass sie den Bedürfnissen der Grafiker entsprechen; Das heißt, Bilder zu reproduzieren, die bereits ordnungsgemäß für das Gerät gerendert wurden, auf dem das Eingabebild erstellt wurde. Das Ziel grafischer GVO ist es, die bestmögliche Reproduktion des Eingabebilds auf dem Ausgabegerät zu ermöglichen. Die neue CTE GBD wurde entwickelt, um vier wichtige Probleme zu lösen.
Da das Eingabebild für das Eingabegerät gerendert wird, passen alle Farben innerhalb des Bereichs zwischen dem Weißpunkt des Mediums und dem Schwarzpunkt. Angenommen, das Bild ist ein Foto einer Szene, in der ein diffuses Weiß vorhanden ist, z. B. eine Person in einem weißen T-Shirt, und ein Glanzlicht, z. B. lichtreflektiert von einem Fenster oder Chromstoßstange. Die Szene wird auf dem Eingabemedium gerendert, sodass die glanzige Hervorhebung dem Weißpunkt des Mediums zugeordnet wird, und das diffuse Weiß wird einer neutralen Farbe zugeordnet, die dunkler ist als der weiße Punkt des Mediums. Die Wahl der Zuordnung von Farben aus der Szene zum Eingabemedium ist sowohl eine szenenabhängige Entscheidung als auch eine ästhetische Entscheidung. Wenn die glanzige Hervorhebung in der originalen Szene fehlte, würde das diffuse Weiß wahrscheinlich dem weißen Punkt des Mediums zugeordnet werden. In einer Szene mit vielen Hervorhebungsdetails würde mehr Bereich zwischen dem Glanzweiß und dem diffusen Weiß gelassen. In einer Szene, in der die Hervorhebung nicht signifikant ist, bleibt möglicherweise sehr wenig Bereich übrig.
Bei vorab gerenderten Bildern ist die Gamutzuordnung relativ einfach. Grundsätzlich wird der weiße Punkt des ursprünglichen Mediums dem Weißen Punkt des Reproduktionsmediums zugeordnet, der schwarze Quellpunkt dem schwarzen Zielpunkt zugeordnet, und der Großteil der Zuordnung ist abgeschlossen. Die verschiedenen GVO bieten Variationen für die Zuordnung anderer Punkte auf der Tonskala des Quellmediums und unterschiedliche Möglichkeiten, chroma-Werte außerhalb des Farbraums zu behandeln. Die Zuordnung von Weiß zu Weiß und Schwarz zu Schwarz ist jedoch in diesen Variationen konsistent. Diese Implementierung erfordert, dass Weiß über einem J* von 50 und schwarz unter einem J* von 50 liegen muss.
Nicht alle Farbcodierungen beschränken die Farbbereiche für Eingabebilder. Die IEC-Standardfarbcodierung scRGB (IEC 61966-2-2) bietet 16 Bits für jeden der drei Farbkanäle Rot, Grün und Blau (RGB). Bei dieser Codierung wird verweisschwarz nicht als RGB-Triple (0, 0, 0) codiert, sondern als (4096, 4096, 4096). Referenzweiß ist codiert als (12288, 12288, 12288). Die scRGB-Codierung kann verwendet werden, um spiegelbezogene Hervorhebungen und Schattendetails darzustellen. Es enthält RGB-Dreifache, die physisch nicht möglich sind, da sie negative Mengen an Licht erfordern, und Codierungen, die sich außerhalb des CIE-Spektral locus befinden. Offensichtlich kann kein Gerät alle Farben im scRGB-Farbraum erzeugen. Tatsächlich kann kein Gerät alle Farben erzeugen, die ein Mensch sehen kann. Daher können Geräte den scRGB-Gamut nicht ausfüllen, und es wäre nützlich, den Teil des Gamuts darzustellen, den sie ausfüllen. Jedes Gerät verfügt über einen Bereich von Werten im scRGB-Bereich, den es erzeugen kann. Dies sind die "erwarteten" Farben für das Gerät; Es wäre für das Gerät überraschend, Farben außerhalb dieses Farbraums zu erzeugen. Es gibt eine definierte Transformation von scRGB-Speicherplatz in Darstellungsraum, sodass jedes Gerät auch einen Bereich von Darstellungswerten aufweist, den es voraussichtlich reproduzieren soll.
Sowohl in scRGB als auch in Eingaben von Erfassungsgeräten, die mit einem festen Ziel gekennzeichnet sind, ist es möglich, einen Wert außerhalb des Bereichs der erwarteten Werte zu erhalten. Wenn jemand eine Kamera auf ein Testziel kalibriert; und erfasst dann eine Szene mit spiegeligen Hervorhebungen. Möglicherweise gibt es Pixel, die heller als der weiße Punkt des Ziels sind. Das gleiche kann passieren, wenn ein natürlich vorkommendes Rot chromatischer ist als das Zielrot. Wenn jemand ein scRGB-Bild von einem Gerät übernimmt und dann die Farben im Bild manuell bearbeitet, ist es möglich, Pixel zu erstellen, die außerhalb des erwarteten Bereichs des Geräteumfangs liegen, obwohl sie sich innerhalb des vollständigen scRGB-Farbraums befinden.
Ein zweites Problem scheint zunächst nicht damit zu zusammenhängen. Dies tritt auf, wenn Sie ein Farbziel verwenden, um ein Eingabegerät zu charakterisieren, z. B. eine Kamera oder ein Scanner. Reflektierende Ziele werden in der Regel auf Papier produziert und enthalten eine Reihe von farbigen Patches. Hersteller stellen Datendateien mit Farbmessungen bereit, die unter einer festen Anzeigebedingung für jeden Farbpatch durchgeführt werden. Farbprofilerstellungstools erstellen eine Zuordnung zwischen diesen Messwerten und den Werten, die von den Farbsensoren in den Geräten zurückgegeben werden. Das Problem besteht darin, dass diese Farbziele häufig nicht den gesamten Bereich der Gerätewerte abdecken. Der Scanner oder die Kamera kann beispielsweise den Wert (253, 253, 253, 253) für den weißen Referenzpunkt zurückgeben, und ein roter Verweisfleck kann den RGB-Wert (254, 12, 4) aufweisen. Diese stellen den Bereich der erwarteten Werte für das Eingabegerät dar, basierend auf den Zielwerten. Wenn Sie das Eingabegerät basierend auf den Antworten auf das Ziel charakterisieren, erwarten Sie nur Farben innerhalb dieses schmalen Bereichs. Dieser Bereich ist nicht nur kleiner als der Farbbereich, den Menschen sehen können, er ist auch kleiner als der Farbbereich, den das Gerät erzeugen kann.
In beiden Fällen ist es schwierig, den Farbraum des Eingabegeräts oder bildes abzuschätzen, obwohl ein Bezugsraum oder messungen vorhanden ist. Im ersten Problem ist der plausible Gamut des Eingabegeräts kleiner als der vollständige Umfang von scRGB. Im zweiten Problem ist der Referenzumfang des Ziels kleiner als der vollständige mögliche Bereich des Eingabegeräts.
Das dritte Problem ist die Tonzuordnung. Es wurden viele Modelle von Gamutgrenzen vorgeschlagen, die vorgerenderte Bilder, die in der Grafik verwendet werden, angemessen darstellen können, z. B. das Braun- und Fairchild-Gebirge (Braun[97]) und Morovics Segment Maxima-Begrenzungsdeskriptor (Morovic[98]). Diese Modelle liefern jedoch nur Informationen über die Extreme des Geräteumfangs; es fehlen Informationen zu anderen Punkten in der Tonabbildung. Ohne solche Informationen können GVO nur grobe Schätzungen der optimalen Tonabbildung vornehmen. Schlimmer noch, diese Modelle bieten keine Hilfe für den erweiterten Dynamikbereich in scRGB und bei Digitalkamerabildern.
Wie wird dieses Problem in der Foto- und Videoindustrie gelöst? Die Kamera erfasst ein Bild. Experten könnten diskutieren, wie viel Rendering im Erfassungsgerät auftritt; aber sie sind sich einig, dass es sich nicht um einen erheblichen Betrag handelt. Beide Technologien ordnen ein diffuses Weiß in einer aufgenommenen Szene nicht dem Weißpunkt des Mediums zu. Ebenso ordnen sie den schwarzen Punkt von der Szene nicht dem schwarzen Punkt des Mediums zu. Das Verhalten des fotografischen Films wird im Dichteraum mithilfe einer charakteristischen Kurve beschrieben, die oft als Hurter- und Driffield-Kurve oder H&D-Kurve bezeichnet wird. Die Kurve zeigt die Dichte der originalen Szene und die resultierende Dichte auf dem Film. Abbildung 18 zeigt eine typische HD-Kurve&. Die x-Achse stellt eine zunehmende Protokollbelichtung dar. Die y-Achse stellt die Dichte auf der Folie dar. Fünf Bezugspunkte sind auf der Kurve markiert: schwarz ohne Detail, das die minimale Dichte auf dem Negativen darstellt; schwarz mit Details; Referenz mittelgrau Karte; weiß mit Details; und weiß ohne Detail. Beachten Sie, dass zwischen Schwarz ohne Detail (das das Geräteschwarz darstellt) und Schwarz mit Details (Schattenschwarz) leer ist. In ähnlicher Weise gibt es Zwischenweiß mit Details (diffuses Weiß) und Weiß ohne Detail (was geräteweiß darstellt).
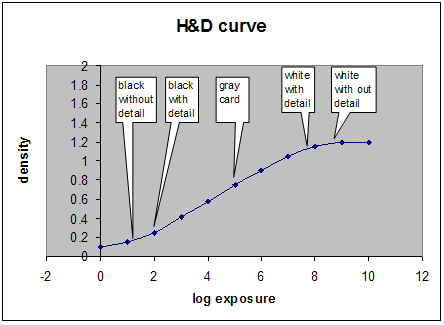
Abbildung 18 : H D-Kurve&für Folienfilm
Die Videobranche bietet "Kopfraum" und "Fußraum" in Bildern. In der ITU 709-Spezifikation wird die Leuchtdichte (Y genannt) in 8 Bits mit einem Bereich von 0 bis 255 codiert. Referenzschwarz ist jedoch mit 15 codiert, und Referenzweiß ist als 235 codiert. Dadurch bleibt der Codierungsbereich zwischen 236 und 255, um spiegelbezogene Hervorhebungen darzustellen.
Die Videobranche präsentiert ein im Wesentlichen geschlossenes System. Obwohl es viele verschiedene Geräteanbieter gibt, basieren Videosysteme auf Referenzgeräten. Es gibt eine Standardcodierung für Videobilder. Es ist nicht erforderlich, eine Gamutgrenze mit Videobildern zu kommunizieren, da alle Bilder für die Wiedergabe auf demselben Referenzgerät codiert sind. Film ist auch closed loop, da es nicht erforderlich ist, Zwischendaten zwischen verschiedenen Komponenten zu vermitteln. Sie möchten eine Lösung, mit der Bilder von Geräten mit unterschiedlichem Farbraum, die sowohl vorab gerenderte als auch nicht gerenderte Szenen darstellen, bei der Ausgabe mit unterschiedlichem Farbraum reproduziert werden können.
Ein viertes Problem, das der neue CTE beheben muss, ist, dass die von einem Gerät erzeugten visuell grauen Farben, z. B. wenn rot=grün=blau auf einem Monitor, häufig nicht auf die neutrale Achse der CAM fallen (wenn die Chroma = 0,0). Dies führt zu großen Schwierigkeiten für GVO. Damit GMAs gut funktionieren, müssen Sie die Beschreibung des Geräteumfangs und der Eingabepunkte so anpassen, dass die neutrale Achse des Geräts auf die neutrale Achse des Erscheinungsbildraums fällt. Sie müssen Punkte von der neutralen Achse um einen ähnlichen Betrag anpassen. Andernfalls können Sie keine reibungslosen Abstufungen durch das Bild vornehmen. Auf dem Weg aus dem GMA machen Sie diese Zuordnung relativ zur neutralen Achse des Ausgabegeräts rückgängig. Dies wird als "chiropraktische" Begradigung der Achse bezeichnet. Wie ein Chiropraktiker richten Sie nicht nur das Skelett (neutrale Achse) auf, sondern passen den Rest des Körpers an, um sich mit dem Skelett zu bewegen. Wie ein Chiropraktiker passen Sie das Skelett nicht um die gleiche Menge durch den gesamten Raum an. Stattdessen passen Sie verschiedene Abschnitte unterschiedlich an.
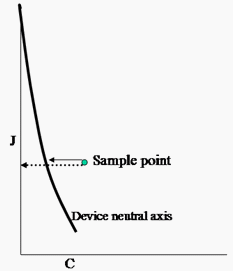
Abbildung 19: Krümmung der geräteneutralen Achse relativ zur neutralen CIECAM-Achse
Das neue CTE erfordert ein Modell einer Gamutgrenze, das verwendet werden kann, um sowohl gerenderte als auch nicht gerenderte Quellbilder darzustellen, Informationen über das Aussehen von geräteneutralen Bildern bereitzustellen und Informationen für Tonbildbilder mit einem breiten Leuchtdichtebereich bereitzustellen.
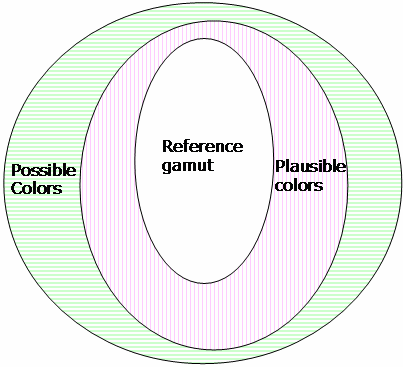
Abbildung 20 : Drei Gamut-Shells
Die Gamutgrenze besteht aus drei Shells, die drei Regionen definieren.
Im neuen CTE wird die äußere Hülle des Gamuts mit einem konvexen Rumpf gebildet, der aus Probenpunkten im Geräteraum hergestellt wird. Ein Rumpf wird gebildet, indem eine Reihe von Probenpunkten genommen und durch eine Oberfläche umgeben wird. Ein konvexer Rumpf hat die zusätzliche Eigenschaft, überall konvex zu sein. Daher ist dies nicht der kleinstmögliche Rumpf, der an die Daten angepasst werden kann. Experimenten haben jedoch gezeigt, dass eine zu enge Anpassung der Beispielpunkte zu unattraktiven Artefakten in Bildern führt, z. B. ein Mangel an glatter Schattierung. Der konvexe Rumpf scheint diese Probleme zu lösen.
Im Algorithmus werden Farbdarstellungswerte für eine Reihe von Punkten abgerufen, die vom Gerät erfasst werden. Bei Monitoren und Druckern werden die Farbdarstellungswerte durch Ausgabe von Beispielen und anschließendes Messen abgerufen. Sie können auch ein Gerätemodell erstellen und dann synthetische Daten über das Gerätemodell ausführen, um Messwerte vorherzusagen. Die Messwerte werden dann vom colorimetrischen Raum (XYZ) in den Darstellungsraum (Jab) konvertiert, und der Rumpf wird um die Punkte gewickelt.
Der wichtigste Punkt für diesen Algorithmus ist, dass der angenommene Weißpunkt, der bei der Konvertierung von Colorimetrie in Darstellungsraum verwendet wird, nicht der Weißpunkt des Mediums sein muss. Stattdessen können Sie einen Punkt weiter innerhalb des Farbraums und auf (oder nahe) der neutralen Achse auswählen. Dieser Punkt weist dann den J-Wert 100 auf. Proben mit einem gemessenen Y-Wert, der höher als der angenommene Weißpunkt ist, erhalten einen J-Wert größer als 100.
Wenn Sie den diffusen Weißpunkt der Szene als den übernommenen Weißpunkt für die Farbraumkonvertierung platzieren, werden spiegelspezifische Highlights in der Szene leicht als J-Wert größer als 100 erkannt.
Da das CIECAM02-Farbmodell auf dem menschlichen visuellen System basiert, wird nach der Auswahl eines übernommenen Weißs automatisch die Helligkeitsstufe des schwarzen Punkts (J = 0) vom Modell bestimmt. Wenn das Eingabebild einen großen dynamischen Bereich aufweist, ist es möglich, dass es Werte gibt, die J-Werten kleiner als 0 zugeordnet sind.
Die folgende Abbildung 21 zeigt die geräteneutralen Elemente, die durch die Mitte der plausiblen Und Referenzskala laufen.
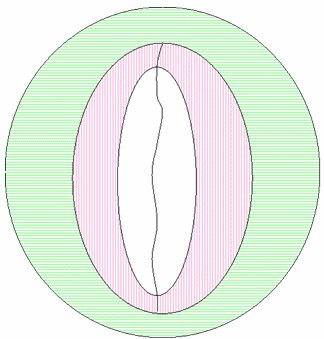
Abbildung 21 : Geräteneutrale Achse zur Gamutgrenze hinzugefügt
Alle Gamutzuordnungen beinhalten entweder das Ausschneiden eines Eingabebereichs in eine Ausgabeskala oder das Komprimieren des Eingaberaums, um in den Ausgaberaum zu passen. Komplexere Algorithmen werden durch Komprimieren und Beschneiden in verschiedene Richtungen oder durch Unterteilen des Gamuts in verschiedene Regionen und anschließendes Ausschneiden oder Komprimieren in den verschiedenen Regionen gebildet.
Die neue CTE erweitert dieses Konzept, um die Regionen eines möglichen Gamuts, eines plausiblen Gamuts und einer Referenzskala zu unterstützen, und ermöglicht es DEN GVO, sie auf unterschiedliche Weise zu erfassen. Darüber hinaus verfügen die GVO über Informationen über die geräteneutrale Achse. Die folgende Diskussion befasst sich mit Situationen, in denen die plausiblen Gamuts und Referenz gamuts aufeinander reduziert sind.
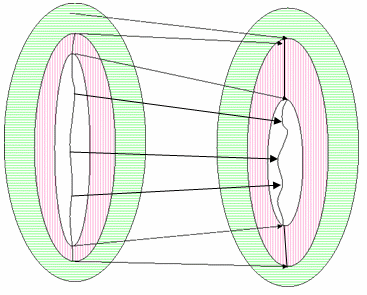
Abbildung 22 : GMA mit zwei nicht reduzierten Gamutdeskriptoren
Dieses Beispiel wird möglicherweise angezeigt, wenn Sie von einem Eingabegerät, z. B. einer Kamera oder einem Scanner, das mit einem reflektierenden Ziel gekennzeichnet ist, dem scRGB-Raum zugeordnet werden. Hier sind die plausiblen Farben, die heller als Referenzweiß sind, glanzliche Hervorhebungen. In der Praxis generiert die Charakterisierung einer Kamera mit einem Ziel möglicherweise nicht den vollständigen Wertebereich, der in der Kamera möglich ist; jedoch würden glanzliche Highlights und sehr chromatische Farben in der Natur gefunden. (Transmissive Ziele verfügen in der Regel über einen Patch, der der minimalen Dichte entspricht, die auf dem Medium möglich ist. Bei einem solchen Ziel würden Glanzlichter in den Bereich des Ziels fallen.) Der Schwarze Verweis für ein reflektierendes Ziel wäre der Anfang des Schattenschwarzbereichs. Das heißt, es gibt wahrscheinlich Farben in den Schatten, die dunkler sind als das Schwarz auf dem Ziel. Wenn das Bild viele interessante Inhalte in dieser Region enthält, kann es sich lohnen, diese tonale Variation beizubehalten.
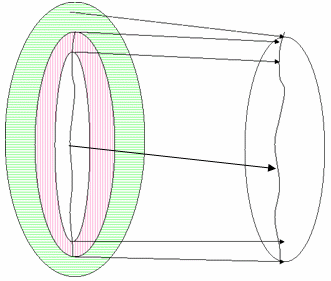
Abbildung 23 : GMA mit reduzierter Zielskala
Abbildung 23 zeigt einen möglichen Gamut-Zuordnungsalgorithmus, wenn die Zielskala nur den Bereich von Weiß bis Schwarz des Geräts bereitstellt und es außerhalb dieses Gamuts keine möglichen Farben gibt. Dies geschieht wahrscheinlich bei typischen Ausgabegeräten, z. B. Druckern. Die möglichen Farben werden dem Rand des Zielbereichs zugeordnet. Es fehlt jedoch eine Tonkurve für das Ausgabegerät. Der GMA muss einen neutralen Punkt mit niedrigerer Leuchtdichte auswählen, um als Zuordnungsziel für das Referenzweiß zu verwenden. Ein ausgereifter Algorithmus kann dies tun, indem er die Helligkeiten im Quellbild histogrammiert und sieht, wie viele im erwarteten Bereich fallen, aber heller als die Referenz weiß. Je mehr Leichtigkeit, desto mehr Platz auf dem Zielgerät ist zwischen den zugeordneten Punkten für die Glanzlichter und referenziertem Weiß erforderlich. Ein einfacherer Algorithmus kann einen beliebigen Abstand von der Helligkeitsskala des Geräts auswählen, z. B. 5 Prozent. Ein ähnlicher Ansatz gilt für die Zuordnung des maximalen Schwarz- und Schattenschwarzens.
Nachdem Sie die Zieltonkurve generiert haben, können Sie eine Methode ähnlich der in der vorherigen Abbildung 23 verwendeten Methode zuordnen. Alle Punkte in der Zieltonkurve fallen innerhalb der Geräteskala, und alle Punkte in der Zuordnung müssen innerhalb der Geräteskala liegen.
Wenn Sie die linken und rechten Abbildungen sowie die Richtungen der Pfeile in Abbildung 23 umkehren, können Sie den Fall beschreiben, in dem das Quellbild nur einen Referenzumfang aufweist und die drei Gamuts des Ausgabegeräts nicht aufeinander reduziert sind. Ein Beispiel hierfür ist die Zuordnung von einem Monitor zu scRGB. Auch hier muss der GMA die Kontrollpunkte für die fünf Punkte in der Tonkurve für das Quellbild synthetisieren. Bei einigen Zuordnungen können alle Punkte der Tonkurve innerhalb des scRGB-Geräteumfangs platziert werden, während andere Zuordnungen einen größeren Teil des scRGB-Gamuts verwenden können, indem diffuses Weiß dem Referenzweiß zugeordnet wird und das Glanzweiß einem helleren Wert zugeordnet werden kann.
Schließlich haben Sie den Fall, dass beide Geräte nur über die Referenzskala verfügen, wodurch die meisten Gamut-Zuordnungsalgorithmen funktionieren. Sie können dies also beheben, indem Sie einfach auf aktuelle Algorithmen zurückgreifen. Wenn Sie eine vernünftige Möglichkeit haben, die fünf Referenzpunkte für die Quell- und Zielgeräte zu bestimmen, können Sie die Referenzpunkte auch zuordnen.
Geräte gamuts enthalten mehr als die fünf Bezugspunkte auf der neutralen Achse. Diese stellen lediglich die Grenzen zwischen potenziellen Regionen im Bild dar. Zwischen den einzelnen Bezugspunkten können Sie eine der vorhandenen Verfahren für die Gamutzuordnung verwenden. Sie können also den Bereich unerwarteter Farben ausschneiden und alle Farben zwischen dem erwarteten Weiß und Schwarz komprimieren, oder Sie können alle Farben außerhalb des Referenzbereichs abschneiden und innerhalb dieses Bereichs komprimieren. Es gibt viele Möglichkeiten, die in verschiedenen GVO implementiert werden können. Darüber hinaus können die GVO auf unterschiedliche Weise komprimieren und beschneiden. Alle diese Kombinationen sind im Rahmen dieser Erfindung abgedeckt.
Bisher wurde der Gamut in dieser Diskussion so behandelt, als ob es sich ausschließlich um eine Funktion des Geräts handelte, auf dem das Bild erstellt, erfasst oder angezeigt wurde. Es gibt jedoch keinen Grund, warum alle Bilder für ein Gerät den gleichen Gamut aufweisen müssen. Die GVO hängen von den Daten in der GBD ab. Wenn der Deskriptor zwischen Bildern geändert wird, gibt es keine Möglichkeit für die GVO zu wissen. Insbesondere wenn Bilder keine glanzlichen Hervorhebungen aufweisen, sind GVO besser, wenn der Gamutdeskriptor nicht anzeigt, dass Farben heller als diffuses Weiß sind.
In der neuen CTE-Architektur ist es möglich, mehr als ein GMA zu verwenden. Die Verwendung mehrerer GVO ist von Natur aus falsch definiert. Wenn ein Erfassungsgerät beispielsweise einem GMA sein "Aussehen und Verhalten" zuordnet, tendiert es dazu, dies mit einer zielgenauen Zielskala zu tun. Gleiches gilt für Ausgabegeräte und "zielorientierte" Quellgamuts. Der sRGB-Gamut ist ein häufig angedeutetes, impliziertes Gamut. Daher wird dringend empfohlen, ein einzelnes GMA zu verwenden, wenn vorhersagbar ist. Ein einzelner GMA-Workflow sollte die Standardeinstellung für alle Workflows sein, insbesondere für Consumer- und Prosumerworkflows. Während die Gamut-Zuordnung für die bevorzugte Reproduktion einmal erfolgen sollte, gibt es Fälle, in denen mehrere Zuordnungsprozesse enthalten sind. Zunächst führen Sie für die Prooferstellung eine bevorzugte Zuordnung zum Gamut des endgültigen Zielgeräts und dann ein farbmetrisches Rendering für die Bandbreite des Korrekturhilfegeräts durch. Zweitens werden einige Arten von Zuordnungen verwendet, um die Merkmale des Bilds zu ändern, sind aber nicht enthalten, um einer Geräteskala zuzuordnen, z. B. die Anpassung der Tonkurve oder der Chromatizität. Wenn mehrere GMAs verwendet werden, verwendet die Transformationsschnittstelle ein Array von gebundenen Gamutzuordnungen, d. h. Gamutkarten, die mit einem Paar von Gamut-Begrenzungsbeschreibungen initialisiert wurden. Wenn mehr als eine Gamutzuordnung vorhanden ist, muss die Eingabe gamut-Grenze für eine erfolgreiche Gamutzuordnung mit der Ausgabe gamut-Grenze des Vorgängers identisch sein.
Die Funktion gerätegmut boundary verwendet die Gerätemodell-Engine und analytische Parameter und leitet eine Farbgeräte-Gamutgrenze ab, die als eine geordnete Vertexliste des konvexen Rumpfs des Geräteumfangs beschrieben wird. Die sortierte Scheitelpunktliste wird in CIEJab gespeichert. Die Struktur der sortierten Vertexliste ist für die Hardwarebeschleunigung durch DirectX optimiert. Dieser Ansatz hat viele bekannte Lösungen (suchen Sie im Web nach "konvex hull DirectX" und Sie erhalten weit über 100 Treffer). Es gibt auch eine Referenz aus dem Jahr 1983 zu diesem Thema (Computer Graphics Theory and Application, "Shiphulls, b-spline surfaces and cadcam" S. 34-49), mit Referenzen aus den Jahren 1970 bis 1982 zum Thema.
Zwei verschiedene Techniken können verwendet werden, um die Dreiecke in der Gamut-Shell zu berechnen. Für andere Geräte als additive RGB-Geräte berechnen Sie einen konvexen Rumpf. Sie können die nicht konvexe Hüllenunterstützung für andere Geräte untersuchen, wenn Sie direkten Zugriff auf solche Geräte haben, um die Stabilität, Leistung und Genauigkeit der Algorithmen zu überprüfen. Dies ist ein bekannter Prozess, der keine weitere Beschreibung erfordert. Die für additive RGB-Geräte verwendete Technik wird wie folgt beschrieben.
Verschiedene GBDs haben Vor- und Nachteile. Die konvexe Rumpfdarstellung garantiert schöne geometrische Eigenschaften, z. B. konvexe Farbschnitte, die einen einzigartigen Schnittpunkt mit einem Strahl bieten, der von einem Punkt auf der neutralen Achse ausgeht. Der Nachteil der konvexen Rumpfdarstellung ist auch Konvexität. Es ist bekannt, dass viele Geräte, insbesondere Anzeigegeräte, weit davon entfernt sind, konvex zu sein. Wenn der tatsächliche Gamut erheblich von der Konvexitätsannahme abweicht, wäre die konvexe Rumpfdarstellung ungenau, möglicherweise in dem Maße, in dem sie nicht die Realität darstellt.
Nachdem Sie eine GBD übernommen haben, die eine einigermaßen genaue Darstellung des tatsächlichen Gamuts bietet, treten andere Probleme auf, einige aufgrund des Konzepts des Farbtonschnitts. Es gibt mindestens zwei pathologische Situationen. In der folgenden Abbildung 24 führt ein CRT-Gamut zu Farbschnitten mit "Inseln". In Abbildung 25 führt ein Drucker gamut zu einem Farbschnitt, bei dem ein Teil der neutralen Achse fehlt. Die pathologischen Farbtonscheiben werden in diesen Fällen nicht durch besonders pathologische Gamutgrenzen verursacht. Sie werden durch das Konzept des Farbschnitts verursacht, da (a) es entlang eines konstanten Farbtons genommen wird und (b) nur die Hälfte der Ebene benötigt, die dem Farbtonwinkel entspricht.
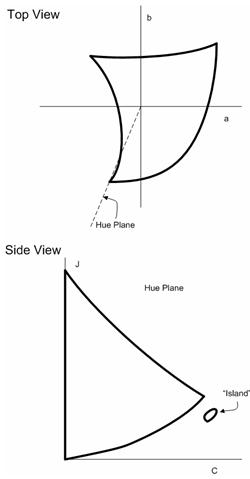
Abbildung 24 : Ein typischer CRT-Monitor hat einen Gamut, der in den Blautönen eine eigenartige "Krümmung" zeigt. Wenn Farbtonscheiben innerhalb dieses Farbtonbereichs verwendet werden, können isolierte Inseln in den Farbtonscheiben angezeigt werden.
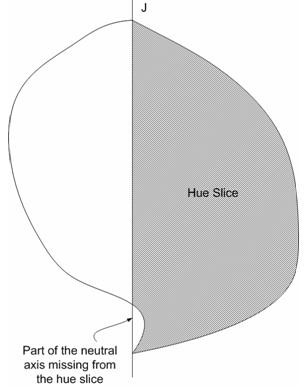
Abbildung 25 : Ein Drucker kann einen Gamut aufweisen, der eine "Lücke" in seiner neutralen Achse aufweist. Wenn ein Farbschnitt genommen wird (der nur die Hälfte der Ebene ist), gibt es eine "Beulen" auf dem Teil der Grenze, der die neutrale Achse ist. Dies kann algorithmisch schwer aufzulösen sein.
Um diese Pathologien zu beheben, wird ein neues Framework vorgeschlagen, das das Konzept des Farbschnitts aufgibt, das als Ausgangspunkt verwendet wurde. Stattdessen verwendet das Framework den Satz von "Begrenzungslinienelementen" oder Linien, die auf der Gamutgrenze liegen. Sie bieten nicht unbedingt eine kohärente geometrische Visualisierung wie Farbschnitte, aber sie unterstützen alle gängigen Gamut-Operationen. Neben der Lösung der zuvor erwähnten Probleme deutet dieser Ansatz auch darauf hin, dass die Konstruktion von Farbtonscheiben, selbst wenn es möglich ist, rechenintensiv ist.
Triangulation der Gamut-Grenze
Ausgangspunkt ist eine GBD, die aus einer Triangulation der Gamutgrenze besteht. Bekannte Methoden zum Erstellen von GBDs bieten in der Regel diese Triangulation. Aus Gründen der Konkretität wird hier eine Methode zum Erstellen von GBDs für additive Geräte und deren Geräteraum beschrieben. Zu diesen Geräten gehören Monitore (sowohl CRT- als auch LCD-basiert) und Projektoren. Die einfache Geometrie des Würfels ermöglicht es Ihnen, ein reguläres Gitter auf dem Cube einzuführen. Die Begrenzungsflächen des Würfels können auf verschiedene Arten trianguliert werden, z. B. die in Abbildung 26 gezeigte. Die Architektur stellt entweder ein Gerätemodell für das Gerät bereit, damit farbmetrische Werte der Gitterpunkte algorithmisch abgerufen werden können, oder messungen wurden direkt für diese Punkte vorgenommen. Die Architektur bietet auch CIECAM02, sodass Sie davon ausgehen können, dass die Startdaten bereits im CIECAM02 Jab-Raum zugeordnet wurden. Dann verfügt jeder Gitterpunkt auf den Begrenzungsflächen des RGB-Cubes über einen entsprechenden Punkt im Jab-Raum. Die Verbindungen von Punkten, die die Gruppe von Dreiecken im RGB-Raum bilden, induzieren auch eine Reihe von Dreiecken im Jab-Raum. Dieser Satz von Dreiecken bildet eine vernünftige Triangulation der Gamutgrenze, wenn (a) das Gitter auf dem RGB-Würfel fein genug ist und (b) die Transformation vom Geräteraum in den einheitlichen Farbraum toplogisch gut ist; Das heißt, es ordnet Grenze zu Grenze zu und dreht den Gamut nicht von innen heraus, sodass innere Punkte zu Begrenzungspunkten werden.
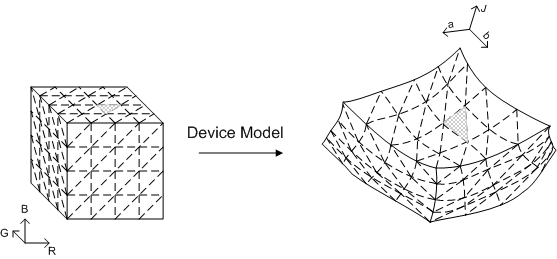
Abbildung 26 : Eine einfache Methode zum Triangulieren der Gamutgrenze eines Geräts mit RGB als Gerätebereich
Begrenzungslinienelemente
Im Mittelpunkt dieses Rahmens steht das Konzept der Begrenzungslinienelemente; eine Reihe von Liniensegmenten, die (a) auf der Gamutgrenze liegen und (b) auf einer Ebene liegen. In diesem Fall ist die Ebene eine Farbtonebene. Jedes Liniensegment ist das Ergebnis einer Schnittmenge der Ebene mit einem Gamut-Begrenzungsdreieck. Obwohl viele Forscher die Konstruktion der Überschneiden einer Ebene mit Begrenzungsdreiecken verwendet haben, analysieren sie im Allgemeinen die Beziehung zwischen diesen Liniensegmenten und versuchen, aus den Liniensegmenten ein kohärentes geometrisches Objekt zu konstruieren. Verschiedene Algorithmen wurden entwickelt, um diesen Zeilensegmenten nacheinander zu folgen, bis ein ganzer Farbausschnitt erhalten wird, und es wurden viele Versuche unternommen, den Suchvorgang zu beschleunigen.
Dieser Ansatz ist anders. Sie überschneiden die Ebene mit den Dreiecken, um die Liniensegmente abzurufen. Anschließend betrachten Sie diese Zeilensegmente als grundlegende konzeptionelle Objekte. Es ist notwendig, die Beziehung zwischen den Liniensegmenten zu analysieren; Sie müssen nicht wissen, wie sie miteinander verbunden sind. Dieser Standpunkt löst das Problem des Farbschnitts mit Inseln. Bei den bekannten Ansätzen, bei denen versucht wird, einen Farbschnitt zu erstellen, wird davon ausgegangen, dass, wenn man mit einem Zeilensegment beginnt und dem nächsten Zeilensegment folgt usw. es führt schließlich zurück zum Ausgangspunkt, an dem ein ganzer Farbschnitt erstellt wird. Leider würde dieser Ansatz die Insel (und im schlimmsten Szenario den Kontinent) verpassen. Indem sie nicht darauf bestehen, ein kohärentes geometrisches Bild zu erhalten; Das heißt, Hue Slice, sie können das Inselproblem mühelos bewältigen. Ein weiterer wichtiger Unterschied in diesem Ansatz besteht darin, dass zur Beschleunigung der Konstruktion von Liniensegmenten ein "Dreieckfilter" verwendet wird. Der Dreieckfilter löst bestimmte Dreiecke aus, die definitiv keine Liniensegmente erzeugen, die im aktuellen Gamut-Vorgang nützlich wären. Da das Kreuzen eines Dreiecks mit der Ebene rechenintensiv ist, verbessert dies die Geschwindigkeit. Ein Nebeneffekt ist, dass Sie farbliche Segmente nicht erstellen können, da einige Liniensegmente aufgrund der Dreiecksfilterung fehlen würden.
Gamut-Vorgang: CheckGamut
Im folgenden Beispiel wird erläutert, wie das Framework funktioniert und wie CheckGamut ausgeführt wird, d. h. der Vorgang der Überprüfung, ob eine Farbe in der Farbskala enthalten ist.
Das allgemeine Framework ist in der folgenden Abbildung 27 dargestellt. Es gibt verschiedene Komponenten. Die kursiv beschrifteten Komponenten sind Komponenten, die sich in der Implementierung je nach dem betreffenden Gamut-Vorgang unterscheiden können. Die anderen Komponenten sind in allen Gamutvorgängen invariant. Zunächst besteht die Eingabe aus einer Reihe von Farbattributen. Im Fall von CheckGamut ist dies die Abfragefarbe. In Abbildung 27 und der folgenden Erläuterung wird davon ausgegangen, dass der Farbtonwinkel entweder zu den Eingabefarbattributen gehört oder daraus abgerufen werden kann. Dies ist eindeutig der Fall, wenn die Eingabe der gesamte Farbpunkt ist, entweder in Jab oder JCh, aus dem Sie dann den Farbtonwinkel berechnen können. Beachten Sie, dass der Farbtonwinkel nur benötigt wird, weil Farbtonebenen verwendet werden. Abhängig vom betreffenden Gamut-Vorgang ist es möglicherweise nicht erforderlich, die Farbtonebene zu verwenden. Bei der Konstruktion der Routine checkGamut können Sie beispielsweise Ebenen der Konstanten J verwenden. Dies ist eine Allgemeinheit, die nicht weiter verwendet oder erörtert wird; Es kann jedoch hilfreich sein, sich an diese Flexibilität der Methodik zu erinnern, um andere Gamut-Vorgänge zu unterstützen, wenn die Farbtonebene möglicherweise nicht die beste Wahl ist.
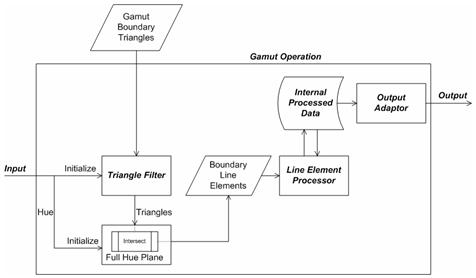
Abbildung 27 : Das Framework zur Unterstützung von Gamut-Vorgängen
Der Farbtonwinkel, der direkt aus den Eingaben abgerufen oder aus den Eingaben berechnet wird, wird verwendet, um die Farbtonebene mit der Bezeichnung Full Hue Plane in der Abbildung zu initialisieren. "Full" wird betont, weil dies die vollständige Ebene ist, nicht nur die halbe Ebene, die den Farbton enthält. Die vollständige Ebene enthält sowohl den Eingabefarbwinkel als auch den 180 Grad entgegengesetzten Winkel. Die wichtigste Funktionalität der Farbtonebene ist die Intersect-Funktion, die im folgenden Unterabschnitt, Full Hue Plane: Intersect, erläutert wird. Angenommen, die GBD wurde bereits erstellt, und der Satz von Gamut-Begrenzungsdreiecks ist verfügbar. Kreuzen Sie die Dreiecke, die den Dreiecksfilter erhalten haben, mit der Farbtonebene, indem Sie sich kreuzen. Die Dreieckfilterkomponente wird kursiv beschriftet, was bedeutet, dass die Komponente in der Implementierung für verschiedene Gamutvorgänge variiert. Der Dreiecksfilter für CheckGamut wird im Abschnitt Gamut Operation: CheckGamut (Fortsetzung) erläutert. Das Ergebnis der Überschneiden eines Dreiecks mit der Farbtonebene ist entweder leer oder ein Boundary Line-Element , d. h. ein Paar unterschiedlicher Punkte. Wenn das Ergebnis nicht leer ist, wird es an den Zeilenelementprozessor übergeben, der je nach Gamut-Vorgang wiederum unterschiedliche Aktionen ausführt. Der Zeilenelementprozessor aktualisiert die interne Datenstruktur Internal Processed Data , deren Inhalt oder Layout ebenfalls vom Gamut-Vorgang abhängt. Im Allgemeinen enthalten die intern verarbeiteten Daten die "Antwort" auf das Problem, die mit jedem neu gefundenen Boundary Line-Element ständig aktualisiert wird. Nachdem alle Begrenzungslinienelemente verarbeitet wurden, wurde die Antwort gefunden. Es bleibt, über den Ausgabeadapter darauf zuzugreifen. Da die internen verarbeiteten Daten spezifisch für den Gamut-Vorgang sind, ist der Ausgabeadapter auch spezifisch für den Gamut-Vorgang.
Vollständige Farbtonebene: Schnittmenge
Die Intersect-Funktion berechnet den Schnittpunkt der Farbtonebene und eines Dreiecks. So einfach es klingt, ist diese Funktion aus zwei Gründen wichtig.
Erstens kann die Überschneidung jeder Kante des Dreiecks mit der Ebene drei Schnittpunkte ergeben, eine geometrisch unmögliche Situation. Der Grund, warum dies bei der Berechnung passieren kann, ist, dass bei Berechnungen in Gleitkomma, z. B. im IEEE-Format, in jedem Schritt Unsicherheiten oder "numerisches Rauschen" vorhanden sind, die die Schlussfolgerung beeinflussen, ob eine Kante die Ebene überschneidet. Wenn die Ebene die Kanten in einer Nahverfehlungssituation überschneidet, sind die Schnittpunkte nah beieinander, und die Bestimmung, ob ein Schnittpunkt innerhalb der Kante liegt, ist zufällig. Obwohl das Rauschen in den numerischen Werten der Punkte klein ist, ist die qualitative Schlussfolgerung, dass es mehr als zwei Schnittpunkte gibt, geometrisch unmöglich und im Algorithmus schwer zu behandeln.
Zweitens befindet sich diese Funktion in der kritischen Schleife für jede Kante jedes gefilterten Dreiecks, daher ist es wichtig, dass Sie die Effizienz so weit wie möglich optimieren.
Um das erste Problem numerischer Rauschen zu beheben, führen Sie die Berechnungen in ganzen Zahlen aus. Um das zweite Problem der Effizienzoptimierung zu beheben, speichern Sie das am häufigsten verwendete Attribut jedes Scheitelpunkts oder das "Punktprodukt", das jedem Scheitelpunkt zugeordnet ist. Die Übergabe in ganze Zahlen ist eine typische Möglichkeit, um geometrische Konsistenz zu gewährleisten. Die Grundidee ist, dass, wenn Sie quantisieren müssen, dies am Anfang tun. Dann können nachfolgende Berechnungen in ganzen Zahlen durchgeführt werden, und wenn die ganzen Zahlen breit genug sind, damit keine Überlaufgefahr besteht, können die Berechnungen mit unendlicher Genauigkeit durchgeführt werden. Die folgende Quantisierungsfunktion ist für diesen Zweck nützlich.
ScaleAndTruncate(x) = Integer-Teil von x*10000
Der Skalierungsfaktor 10000 bedeutet, dass die Eingabe-Gleitkommazahl über vier Dezimalstellen verfügt, was für diese Anwendung genau genug ist. Abhängig vom Wertebereich des Farbdarstellungsbereichs möchten Sie einen ganzzahligen Typ mit Bits auswählen, die breit genug sind, um die Zwischenberechnungen aufzunehmen. In den meisten Farbdarstellungsräumen liegt der Bereich jeder Koordinate im Bereich von -1.000 bis 1.000. Die quantisierte Koordinate hat einen maximal möglichen absoluten Wert von 1.000*10.000 = 10.000.000. Wie Sie sehen werden, ist die Zwischenmenge ein Punktprodukt, das eine Summe aus zwei Produkten von Koordinaten ist, sodass sie einen maximalen absoluten Wert von 2*(10.000.000) ² = 2?10 ₁₄ hat. Die anzahl der erforderlichen Bits ist log ² (2?10 ₁₄ ) = 47,51. Eine praktische Wahl für den Ganzzahltyp sind daher 64-Bit-Ganzzahlen.
Um sicherzustellen, dass die Überschneidung einer Ebene mit einem Dreieck immer entweder eine leere Menge oder eine Reihe von zwei Punkten ergibt, müssen Sie das Dreieck als Ganzes betrachten, nicht als einzelne Kanten des Dreiecks separat. Um die geometrische Situation zu verstehen, betrachten Sie die "signierten Entfernungen" der Scheitelpunkte des Dreiecks von der Farbtonebene. Berechnen Sie diese signierten Entfernungen nicht direkt; berechnen Sie stattdessen die Punktprodukte der Positionsvektoren der Scheitelpunkte mit dem quantisierten Normalvektor zur Ebene. Genauer gesagt, während der Initialisierung der Farbtonebene wird der quantisierte Normalvektor wie folgt berechnet.
NormalVector = (ScaleAndTruncate(-sin(hue)), ScaleAndTruncate(cos(hue)))
Beachten Sie, dass es sich bei diesem Vektor um einen zweidimensionalen Vektor handelt. Sie können einen zweidimensionalen Vektor verwenden, da die Farbtonebene vertikal ist, sodass die dritte Komponente des normalen Vektors immer null ist. Darüber hinaus wird eine Nachschlagetabelle mit Punktprodukten initialisiert, um einen Eintrag für jeden Scheitelpunkt aus den Gamut-Begrenzungsdreiecken und das entsprechende Punktprodukt auf einen ungültigen Wert festzulegen.
Während eines Vorgangs der Schnittmenge der Farbtonebene mit einem Dreieck wird das Punktprodukt jedes Scheitelpunkts des Dreiecks nach oben gesucht. Wenn der Wert in der Nachschlagetabelle der ungültige Wert ist, wird das Punktprodukt mit dem folgenden Ausdruck berechnet.
NormalVector.a*ScaleAndTruncate(vertex.a) + NormalVector.b*ScaleAndTruncate(vertex.b)
Auch hier wird die J-Komponente des Scheitelpunkts nie verwendet, da der normale Vektor horizontal ist. Dieses Punktprodukt wird dann in der Nachschlagetabelle gespeichert, sodass es nicht erneut berechnet werden muss, wenn das Punktprodukt des Scheitelpunkts später abgefragt wird.
Das Zwischenspeichern ermöglicht eine schnelle Bestimmung, ob sich eine Kante über die Ebene schneidet, nachdem die Punktprodukte in der Nachschlagetabelle tabellariert wurden, die schrittweise erstellt wird, während die Scheitelpunkte verarbeitet werden.
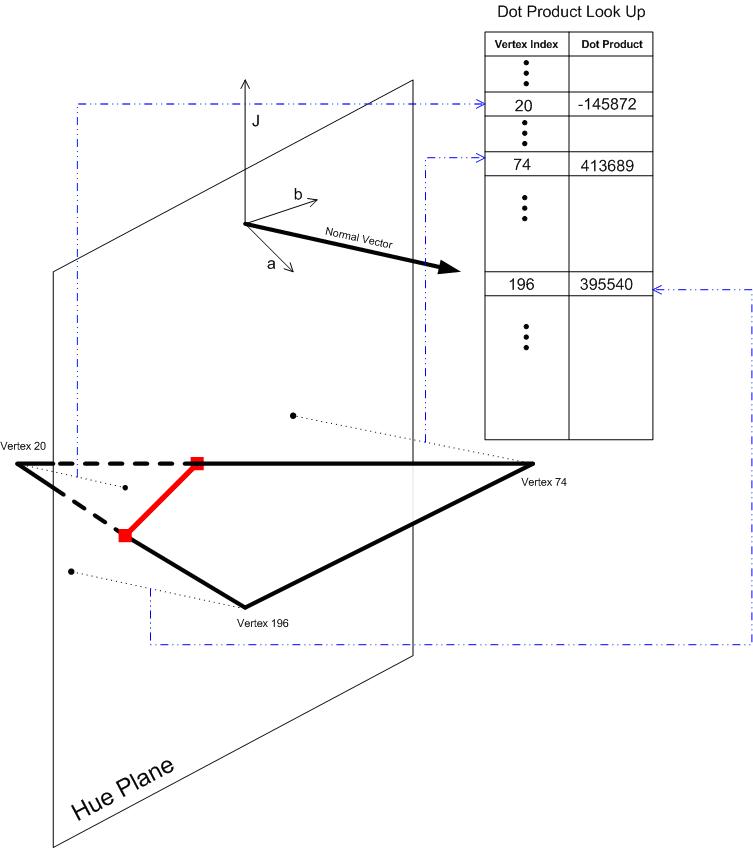
Abbildung 28 : Schnitt der Farbtonebene mit einem Dreieck
Damit das Dreieck in Abbildung 28 die Farbtonebene in einem nicht degenerierten Liniensegment überschneiden kann, müssen sich die Punktprodukte der Scheitelpunkte in aufsteigender Reihenfolge in einem der folgenden Muster befinden.
0,0,+; -,0,0; -,0,+; -,-,+; -,+,+
Ein Endpunkt des Liniensegments entsteht, wenn die Ebene von einer Kante mit Scheitelpunkten überschneiden wird, die im Punktprodukt unterschiedliche Zeichen aufweisen. Wenn das Zeichen null ist, liegt der Scheitelpunkt direkt auf der Ebene, und der Schnittpunkt des Rands mit der Ebene ist der Scheitelpunkt selbst. Beachten Sie auch, dass die Fälle 0,0,0; -,-,0; 0,+,+ werden nicht gemeldet. Der erste Fall (0,0,0) bedeutet, dass das gesamte Dreieck auf der Ebene liegt. Dies wird nicht gemeldet, da jeder Rand des Dreiecks zu einem benachbarten Dreieck gehören sollte, das nicht auch vollständig auf der Ebene liegt. Der Rand wird gemeldet, wenn dieses Dreieck berücksichtigt wird. Die anderen beiden Fälle (-,-,0 und 0,+,+) entsprechen der geometrischen Konfiguration, dass das Dreieck die Ebene in einem Scheitelpunkt berührt. Diese Fälle werden nicht gemeldet, da sie kein nicht degenerates Liniensegment hervorrufen.
Der vorangehende Algorithmus bestimmt, wann eine Schnittmenge zwischen einem Rand des Dreiecks und der Farbtonebene berechnet wird. Nachdem eine Kante bestimmt wurde, wird die Schnittmenge mithilfe parametrischer Formeln berechnet. Wenn eines der Punktprodukte null ist, ist die Schnittmenge der Scheitelpunkt selbst, sodass keine Berechnung erforderlich ist. Unter der Annahme, dass beide Punktprodukte der Scheitelpunkte der Kante ungleich 0 (null) sind, ist Vertex1 der Scheitelpunkt mit dem negativen Punkt produkt dotProduct1; und vertex2 ist der Scheitelpunkt mit positivem Punkt produkt dotProduct2. Diese Reihenfolge ist wichtig, um sicherzustellen, dass der berechnete Schnittpunkt nicht davon abhängt, wie die Reihenfolge der Scheitelpunkte in der Darstellung der Kante angezeigt wird. Das geometrische Konzept der Kante ist symmetrisch hinsichtlich seiner Scheitelpunkte. Der berechnungstechnische Aspekt der Verwendung parametrischer Gleichungen der Kante führt zu Asymmetrie (Wahl des Startvertex), die aufgrund des numerischen Rauschens und der Konditionierungen der zu lösenden linearen Gleichungen einen etwas anderen Schnittpunkt ergeben kann. Mit diesem gesagt, wird der Schnittpunkt, Schnittpunkt, durch folgendes angegeben.
t = dotProduct1/(dotProduct1 - dotProduct2)
Schnittpunkt. J = vertex1. J + t * (vertex2. J – vertex1. J)
intersection.a = vertex1.a + t * (vertex2.a - vertex1.a)
intersection.b = vertex1.b + t * (vertex2.b - vertex1.b)
Gamut-Vorgang: CheckGamut (Fortsetzung)
Der grundlegende geometrische Algorithmus, der für die Gamutüberprüfung verwendet wird, besteht darin, die Anzahl der Strahlenübergänge zu zählen. Betrachten Sie für einen bestimmten Abfragepunkt einen Strahl, der mit dem Abfragepunkt beginnt und nach oben zeigt (J-Richtung). Zählen Sie, wie oft dieser Strahl die Gamutgrenze überschreitet. Wenn diese Zahl gerade ist, ist der Abfragepunkt außerhalb des Bereichs. Wenn diese Zahl ungerade ist, befindet sich der Punkt darin. Im Prinzip kann dieser Algorithmus in 3D implementiert werden, er ist in der Regel von Schwierigkeiten geplagt, die durch degenerierte Situationen verursacht werden, wie z. B. der Strahl (teilweise) auf einem Begrenzungsdreieck liegt, oder niederdimensionale Entartung, wie der Strahl, der (teilweise) am Rand eines Begrenzungsdreiecks liegt. Auch in 2D müssen Sie sich mit diesen degenerieren Situationen auseinandersetzen; aber das Problem ist einfacher und wurde in zufriedenstellender Weise angegangen. Siehe [O'Rourke].
Bestimmen Sie für einen bestimmten Eingabepunkt Jab den Farbtonwinkel h wie folgt.
h = atan(b/a),
Initialisieren Sie die Farbtonebene, und bestimmen Sie dann die Begrenzungslinienelemente, die dieser Farbtonebene entsprechen. Da die Begrenzungslinienelemente nur dann relevant sind, wenn sie den Aufwärtsstrahl überschneiden, richten Sie einen Dreiecksfilter ein, um Dreiecke zu entfernen, die Linienelemente enthalten, die den Aufwärtsstrahl definitiv nicht überschneiden. Betrachten Sie in diesem Fall das umgebende Feld des Dreiecks. Der nach oben gerichtete Strahl überschneidet das Dreieck nicht, wenn sich der Abfragepunkt außerhalb des "Schattens" befindet, der durch das begrenzungsfeld geworfen wird, wenn sich eine Lichtquelle direkt darüber befand. Vergrößern Sie dies leicht mit einer vordefinierten Toleranz, um numerisches Rauschen zu ermöglichen, sodass Sie nicht versehentlich Dreiecke wegwerfen, die nützliche Linienelemente liefern könnten. Das Ergebnis ist der in Abbildung 29 dargestellte halb unendliche rechteckige Zylinder. Die Überprüfung, ob sich der Abfragepunkt innerhalb oder außerhalb dieses Zylinders befindet, kann mithilfe einfacher Ungleichheiten effizient implementiert werden.
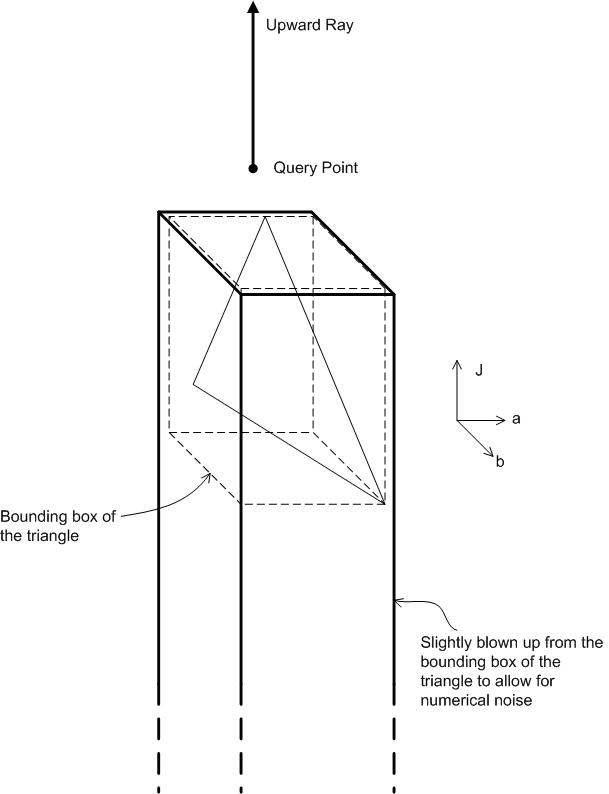
Abbildung 29 : Dreiecksfilter für CheckGamut
CheckGamut verfügt über drei spezifische Komponenten für den Gamut-Vorgang: Interne verarbeitete Daten, Zeilenelementprozessor und Ausgabeadapter. Die internen verarbeiteten Daten sind eine Liste von Zeilenelementen, die vom Zeilenelementprozessor verarbeitet wurden. In diesem Fall fügt der Zeilenelementprozessor der Liste einfach ein Zeilenelement hinzu. Die interne Datenstruktur für interne verarbeitete Daten kann entweder eine verknüpfte Liste oder ein Array sein, das größer werden kann.
Der Ausgabeadapter ist ein Modul, das auf die Liste der Zeilenelemente zugreift und bestimmt, ob ein Linienelement den Aufwärtsstrahl kreuzt (Anzahl 1) oder nicht (Anzahl 0). Das Summieren all dieser Zählungen ergibt eine Gesamtanzahl. Der Ausgabeadapter gibt letztendlich eine Antwort mit "Ja" (In-Gamut) oder "Nein" (außerhalb des Gamuts) aus, je nachdem, ob die Gesamtanzahl ungerade oder gerade ist. Der Schritt, in dem Sie bestimmen, ob ein Linienelement den Aufwärtsstrahl kreuzt, verdient einige Aufmerksamkeit, da hier das Problem der Entartung auftritt und auch das Problem der Überzählung auftritt. Nach [O'Rourke] muss sich der rechte Endpunkt (der Endpunkt mit größerem Chroma) genau auf der rechten Seite des Strahls befinden, damit ein Linienelement den Strahl kreuzt. Dies garantiert, dass, wenn ein Endpunkt jemals genau auf dem Strahl liegt, er nur einmal gezählt wird. Die gleiche Regel löst auch die degenerate Situation, in der das Linienelement genau auf dem Strahl liegt. Sie erhöhen die Anzahl für dieses Zeilenelement nicht.
Abbildung 30 zeigt die resultierenden Linienelemente eines Beispielumfangs mit dem Abfragepunkt an verschiedenen Positionen.
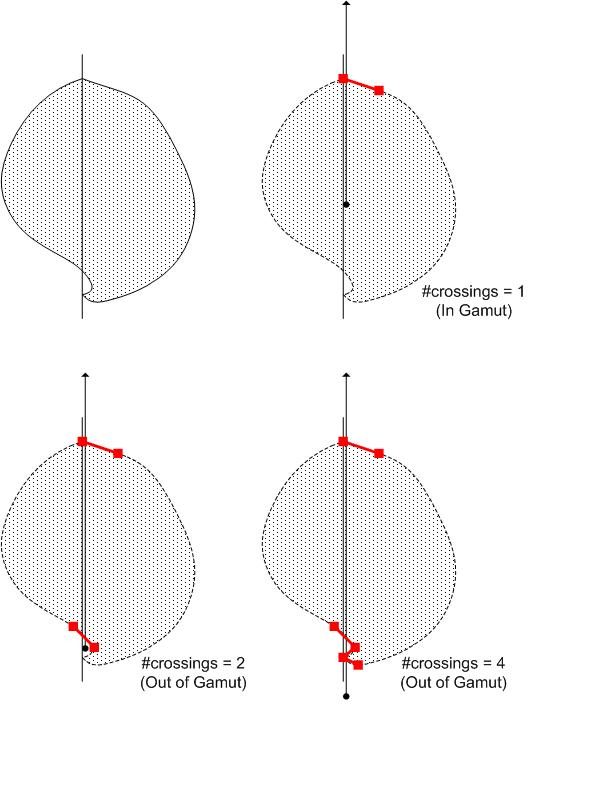
Abbildung 30 : Funktionsweise von CheckGamut
Zuordnung des Mindestfarbunterschieds
Die MinDEMap-Zuordnung des Mindestfarbunterschieds weist eine einfache Spezifikation auf: Wenn sich eine Farbe in der Farbskala befindet, tun Sie nichts. Wenn eine Farbe außerhalb des Farbraums liegt, projizieren Sie sie auf den "nächstgelegenen" Punkt auf der Gamutgrenze. Die Schlüsselwort (keyword) "nächstgelegenen" ist erst gut definiert, wenn Sie die zu verwendende Farbdifferenzgleichung angeben. In der Praxis wird der euklidische Abstand des gewählten Farbdarstellungsraums oder eine Variante davon als Farbdifferenzmetrik verwendet, um die Berechnung einfacher und schneller zu machen. Der Vorteil der euklidischen Metrik ist, dass sie mit dem Punktprodukt des Raums kompatibel ist, wodurch es möglich ist, lineare Algebra zu verwenden. Wenn im Raum ein "Punktprodukt" definiert ist, kann ein Abstand als Quadratwurzel des Punktprodukts des Differenzvektors mit sich selbst definiert werden. Ein Punktprodukt kann im Allgemeinen durch eine positive eindeutige 3x3-Matrix A definiert werden.
u?v = u T Av
wobei die rechte Seite die übliche Matrixmultiplikation ist. Wenn A die Identitätsmatrix ist, wird das Standardpunktprodukt wiederhergestellt. Wenn Jab der Farbraum ist, möchten Sie in der Praxis die Komponenten nicht vermischen, sodass eine andere diagonale Matrix als die Identitätsmatrix verwendet werden kann. Darüber hinaus können Sie die Skalierung auf a und b unverändert lassen, damit das Maß des Farbtons erhalten bleibt. Eine nützliche Variante des euklidischen Standard-Punktprodukts ist die folgende.
w J (J-Komponente von Ihnen)(J-Komponente von v) + (eine Komponente von Ihnen)(eine Komponente von v) + (b-Komponente von Ihnen)(b-Komponente von v)
wobei w J eine positive Zahl ist. Eine weitere Variante besteht darin, w J mit dem Eingabeabfragepunkt variieren zu lassen:
w J\ = w J (queryPoint)
Das Endergebnis ist ein Maß für die Entfernung, die in Bezug auf die beiden Punkte asymmetrisch ist, und mit unterschiedlichen relativen Gewichtungen für Die Leichtigkeit und Farb- oder Farbton, da der Eingabeabfragepunkt variiert. Dies entspricht einigen Beobachtungen über die menschliche Farbwahrnehmung, dass Farbunterschiede nicht in allen Dimensionen gleich gewichtet werden. Es wurde festgestellt, dass Menschen weniger empfindlich auf Unterschiede in der Leichtigkeit als auf Unterschiede in Farbton und Chroma sind.
Die folgende Gewichtungsfunktion ist nützlich.
w J = k ₂ - k ₁ (C - C mₐₓ ) n
wobei k ₂ = 1, k ₁ = 0,75/(C mₐₓ ) n, C mₐₓ = 100, n = 2 und C das kleinere Chroma des Abfragepunkts und C mₐₓ ist.
so, dass ein Gewicht von 0,25 auf den J-Begriff gesetzt wird, wenn die Chroma null ist, und ein Gewicht von 1, wenn chroma 100 ist. Der Trend, J weniger Gewicht auf J zu legen, wenn chroma klein ist, und mehr Gewicht auf J, wenn chroma groß ist, folgt der empfohlenen Verwendung für CMC und CIEDE2000.
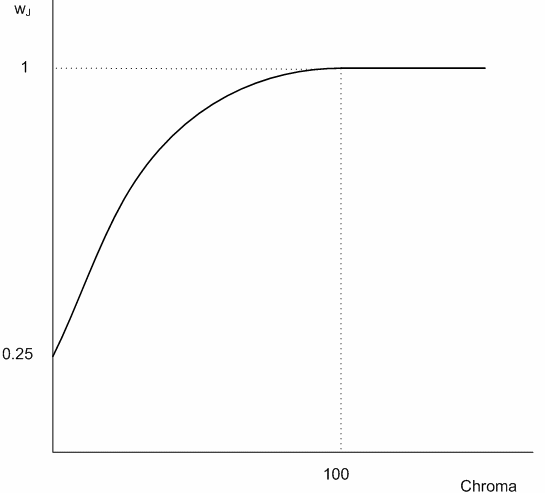
Abbildung 31 : Die Gewichtungsfunktion für die J-Komponente der Metrik
Verwenden Sie für das folgende Beispiel Jab-Speicherplatz. Es ist rechenintensiv, alle Begrenzungsdreiecke zu durchsuchen, um den nächstgelegenen Punkt in der euklidischen Metrik zu ermitteln. Es folgt ein einfacher Ansatz, um diesen Prozess so effizient wie möglich zu gestalten, ohne zusätzliche Annahmen einzuführen, die den Prozess beschleunigen, aber auch nur in einer ungefähren Antwort enden. Zunächst ist es notwendig, die geometrische Prozedur zu verstehen, einen Punkt auf das gegebene Dreieck zu projizieren. Hier finden Sie eine Beschreibung.
Zuerst wird eine orthogonale Projektion auf die unendliche Ebene durchgeführt, die das Dreieck enthält. Die kürzeste Entfernung des Abfragepunkts von der Ebene kann in zwei Schritten bestimmt werden.
(a) Berechnen Sie den Einheits-Normalvektor zum Dreieck.
b) Berechnen des Punktprodukts des Einheits-Normalvektors und eines Vektors, der aus dem Abfragepunkt und einem Punkt auf dem Dreieck gebildet wird; d. h. einer seiner Scheitelpunkte. Da der normale Vektor eine Einheitslänge aufweist, ist der absolute Wert dieses Punktprodukts der Abstand des Abfragepunkts von der Ebene.
Der projizierte Punkt ist möglicherweise nicht die Antwort, da er außerhalb des Dreiecks liegen könnte. Daher müssen Sie zuerst eine Überprüfung durchführen. Die Berechnung entspricht der Berechnung der baryzentrischen Koordinaten des projizierten Punkts relativ zum Dreieck. Wenn der projizierte Punkt als innerhalb des Dreiecks festgelegt wird, ist dies die Antwort. Andernfalls wird der nächstgelegene Punkt an einem der Kanten des Dreiecks erfasst. Führen Sie eine Suche an jedem der drei Kanten durch. Die Bestimmung der Projektion des Abfragepunkts auf eine Kante ist ein Prozess, der der Projektion auf das Dreieck ähnelt, aber eine Dimension weniger. Zunächst wird eine orthogonale Projektion berechnet. Wenn der projizierte Punkt am Rand liegt, ist dies die Antwort. Andernfalls wird der nächstgelegene Punkt an einem der beiden Endpunkte abgerufen. Führen Sie eine Suche nach den beiden Endpunkten durch. Das heißt, berechnen Sie den Abstand des Abfragepunkts von jedem, und vergleichen Sie, welcher kleiner ist.
Eine sorgfältige Untersuchung zeigt, dass es viele wiederholte Suchvorgänge gibt, wenn Sie alle Dreiecke durchlaufen, da eine Kante immer von zwei Dreiecken und einem Scheitelpunkt geteilt wird, der von mindestens drei Kanten geteilt wird. Darüber hinaus sind Sie nicht sehr daran interessiert, den nächstgelegenen Punkt zu einem bestimmten Dreieck zu finden; Sie sind stattdessen daran interessiert, den nächstgelegenen Punkt zur gesamten Gamutgrenze zu finden. Ein bestimmtes Dreieck wäre jedoch das, in dem dies erreicht wird. Es gibt zwei Strategien, die Sie verwenden können, um die Suche zu beschleunigen.
Strategie I. Jeder Scheitelpunkt wird höchstens einmal verarbeitet. Jeder Edge wird höchstens einmal verarbeitet.
Strategie II. Zu jedem Zeitpunkt in der Suche haben Sie einen besten Kandidaten mit der entsprechenden besten Entfernung. Wenn Sie durch eine schnelle Überprüfung feststellen können, dass ein Dreieck nicht in der Lage ist, einen besseren Abstand zu geben, besteht keine Notwendigkeit, die Berechnung weiter fortzusetzen. Sie benötigen nicht den nächstgelegenen Punkt und die entfernung für dieses Dreieck.
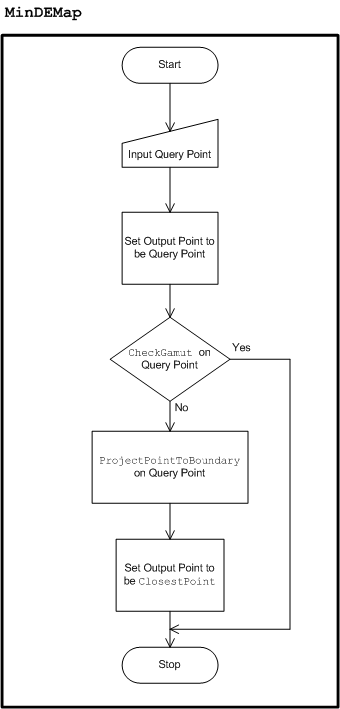
Abbildung 32 : Minimale DE-Zuordnungsschemas
Abbildung 32 zeigt den allgemeinen Logikfluss für die Gamutmap MinDEMap. Für einen Abfragepunkt wird zuerst die CheckGamut-Funktion aufgerufen. Wenn der Punkt in der Übersicht ist, ist die Karte ein No-Op. Wenn der Punkt außerhalb des Gamuts liegt, rufen Sie ProjectPointToBoundary auf. Fahren Sie nun mit Abbildung 33 fort. An diesem Punkt wird davon ausgegangen, dass die folgenden Werte berechnet wurden.
(a) Einheit normaler Vektor zu jedem Gamut-Begrenzungsdreieck in Bezug auf das Standardpunktprodukt.
(b) Vertexliste und Kantenliste zusätzlich zur Dreiecksliste.
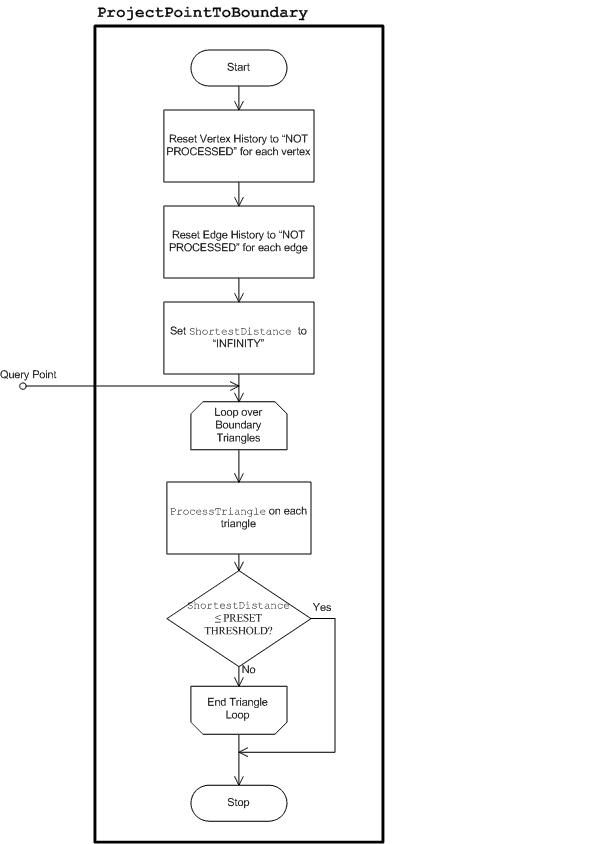
Abbildung 33 : Die ProjectPointToBoundary-Routine
All dies ist ein konstanter Mehraufwand und würde zu geringeren Kosten führen, wenn genügend Abfragen für diese Gamutgrenze durchgeführt werden. In der Regel ist dies der Fall, wenn Sie eine Transformations-LUT von einem Gerät zu einem anderen erstellen, wobei nur zwei feste Gamuts vorhanden sind, und die Transformations-LUT durch Punkte im einheitlich erfassten Raster verläuft. Sie berechnen die normalen Vektoren im Hinblick auf das Standardpunktprodukt vorab, obwohl der Begriff der Senkrechtheit auf dem gewichteten Punktprodukt basiert, das wie zuvor erläutert vom Abfragepunkt abhängt. Der Grund dafür ist, dass ein normaler Vektor in Bezug auf das gewichtete Punktprodukt leicht aus dem Normalvektor bezogen auf das Standardpunktprodukt abgerufen werden kann. Wenn n ₀ ein normaler Vektor in Bezug auf das Standardpunktprodukt ist, dann
n = (J-Komponente von n ₀ /w J, a-Komponente von n ₀, b-Komponente von n ₀ )
entspricht dem Dreieck in Bezug auf das gewichtete Punktprodukt. Aufgrund dieser Beziehung ist es immer noch vorteilhaft, n ₀ vorab zu berechnen, obwohl es basierend auf dem Abfragepunkt angepasst werden muss.
Die ProjectPointToBoundary-Routine beginnt mit dem Zurücksetzen des "verarbeiteten Verlaufs" der Scheitelpunkte und Kanten. Dies sind Tabellen mit BOOLESCHEN Flags, die nachverfolgen, ob ein Scheitelpunkt oder ein Rand zuvor besucht wurde. Außerdem wird die Variable ShortestDistance auf "INFINITY" zurückgesetzt. Dies ist der maximal codierte Wert im verwendeten Gleitkommazahlensystem. Anschließend durchläuft sie eine Schleife und sucht mithilfe des ProcessTriangle-Aufrufs nach dem nächstgelegenen Punkt aus jedem Dreieck. ProcessTriangle ist die Routine zum Aktualisieren der ShortestDistance-Variable und befindet sich eindeutig in der kritischen Schleife. Eine Optimierung besteht darin, zu beenden, wenn das Ergebnis gut genug ist. Nach jedem Aufruf von ProcessTriangle wird die Variable ShortestDistance untersucht. Wenn sie einen vordefinierten Schwellenwert erfüllt, können Sie beenden. Der vordefinierte Schwellenwert hängt vom verwendeten Farbraum und von der erforderlichen Genauigkeit des Farbbildsystems ab. Für eine typische Anwendung möchten Sie keine unnötige Arbeit leisten, wenn der Farbunterschied kleiner ist als das, was vom menschlichen Sehen erkannt werden kann. Bei CIECAM02 beträgt dieser Farbunterschied 1. Verwenden Sie jedoch einen Schwellenwert von 0,005 in der Implementierung, um die Genauigkeit von Berechnungen zu erhalten, da dies möglicherweise nur ein Zwischenschritt in einer Kette von Transformationen ist.
ProcessTriangle implementiert die vorangehende Strategie II. Beim Abrufen eines normalen Vektors vom normal berechneten Einheitsvektor zum Dreieck in Bezug auf das Standardpunktprodukt berechnet er den Abstand des Abfragepunkts zur unendlichen Ebene, die das Dreieck enthält, indem das Punktprodukt des Einheitsvektors und des queryVector, der Vektor aus einem der Scheitelpunkte des Dreiecks, gebildet wird. vertex1, bis zum Abfragepunkt queryPoint.
queryVector = queryPoint – vertex1
Abstand = | normalVector * queryVector |/|| normalVector||
Dies ist eine relativ kostengünstige Berechnung, und die Entfernung ist erforderlich, um weitere Berechnungen durchzuführen. Wenn diese Entfernung nicht kleiner als die aktuelle beste Entfernung ist, ShortestDistance, erzeugt dieses Dreieck keine bessere Entfernung, da es keinen besseren Abstand als die Ebene gibt, die es enthält. In diesem Fall geben Sie die Steuerung zur Dreiecksschleife zurück. Wenn der Abstand kleiner als ShortestDistance ist, haben Sie möglicherweise einen näheren Punkt, wenn dieser Punkt innerhalb des Dreiecks liegt. Sie müssen einige "harte" Berechnungen durchführen (obwohl nichts über lineare Algebra hinausgeht), um dies zu bestimmen. Wenn die anderen beiden Scheitelpunkte des Dreiecks Vertex2 und Vertex3 sind, bilden Sie die Basisvektoren firstBasisVector und secondBasisVector.
firstBasisVector = Vertex2 – Vertex1
secondBasisVector = vertex3 – vertex1
Verwenden Sie das folgende lineare Gleichungssystem, um für unbekannte Sie und v zu lösen.
firstBasisVector * queryVector = (firstBasisVector * firstBasisVector)u + (firstBasisVector * secondBasisVector)v
secondBasisVector * queryVector = (secondBasisVector * firstBasisVector)u + (secondBasisVector * secondBasisVector)v
und die Bedingungen für den projizierten Punkt innerhalb des Dreiecks sind:
0 ≤ u ≤ 1, 0 ≤ v ≤ 1 und Sie + v ≤ 1
Wenn nach dieser Berechnung festgestellt wird, dass der projizierte Punkt innerhalb des Dreiecks liegt, haben Sie einen neuen nächstgelegenen Punkt gefunden. Die Entfernung, die Sie zu Beginn berechnet haben, ist die neu kürzeste Entfernung. Aktualisieren Sie in diesem Fall die Variablen ShortestDistance und ClosestPoint. Wenn der projizierte Punkt außerhalb des Dreiecks liegt, finden Sie möglicherweise einen näheren Punkt an einem seiner Kanten. Daher können Sie die ProcessEdge-Routine an jedem der drei Kanten aufrufen.
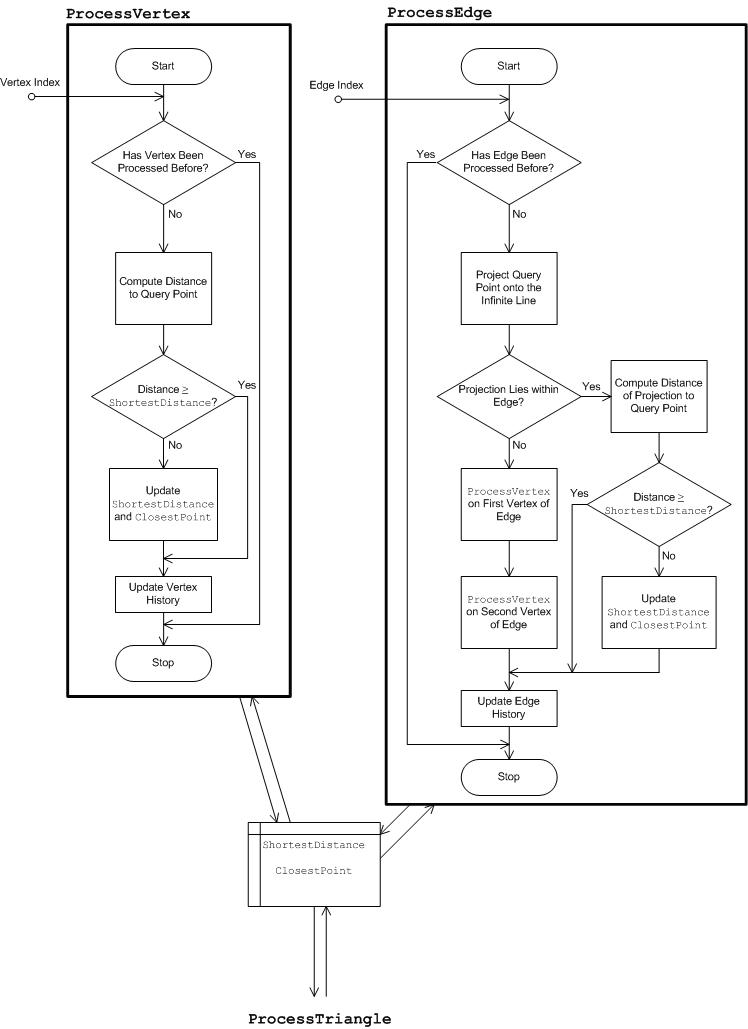
Abbildung 34 : ProcessEdge- und ProcessVertex-Routinen
Die ProcessEdge-Routine implementiert Strategie I, die in Abbildung 34 dargestellt ist. ProcessEdge beginnt mit der Überprüfung, ob der Edge zuvor verarbeitet wurde. Wenn ja, werden keine weiteren Maßnahmen ergriffen. Andernfalls wird die orthogonale Projektion des Abfragepunkts auf die unendliche Linie berechnet, die den Rand enthält. Die lineare Algebra, die an der Berechnung beteiligt ist, ähnelt den vorherigen Dreiecksgleichungen. Die Berechnung ist jedoch einfacher, sie wird hier nicht beschrieben. Wenn der projizierte Punkt innerhalb des Rands liegt, finden Sie den Abstand des projizierten Punkts vom Abfragepunkt. Wenn diese Entfernung kleiner als ShortestDistance ist, haben Sie einen neuen nächstgelegenen Punkt gefunden. Aktualisieren Sie sowohl ShortestDistance als auch ClosestPoint. Wenn der projizierte Punkt außerhalb des Rands liegt, rufen Sie ProcessVertex für die beiden Endpunkte auf. Aktualisieren Sie vor dem Zurückgeben der Steuerung den Edgeverlauf, sodass diese Kante als "VERARBEITET" gekennzeichnet ist.
Schließlich geben Sie eine Beschreibung von ProcessVertex an. Die ProjectVertex-Routine implementiert auch Strategie I und verwaltet eine Vertexverlaufstabelle. Wie in Abbildung 34 dargestellt, wird zunächst überprüft, ob der Scheitelpunkt zuvor verarbeitet wurde. Wenn ja, werden keine weiteren Maßnahmen ergriffen. Andernfalls wird der Abstand des Scheitelpunkts vom Abfragepunkt berechnet. Wenn die Entfernung kleiner als ShortestDistance ist, aktualisieren Sie sowohl ShortestDistance als auch ClosestPoint. Am Ende wird der Vertexverlauf aktualisiert, sodass dieser Scheitelpunkt als "VERARBEITET" gekennzeichnet wird.
Wenn die äußere Steuerungsschleife entweder alle Dreiecke ausgeschöpft oder beendet hat, bevor der Schwellenwert für die Farbdifferenz erreicht wurde, wird auf die Variable ClosestPoint zugegriffen. Dies ist das Ergebnis von MinDEMap. Der Aufrufer kann auch ShortestDistance abrufen, wenn er daran interessiert, wie weit die zugeordnete Farbe von der Abfragefarbe entfernt ist.
Farbtonglättung
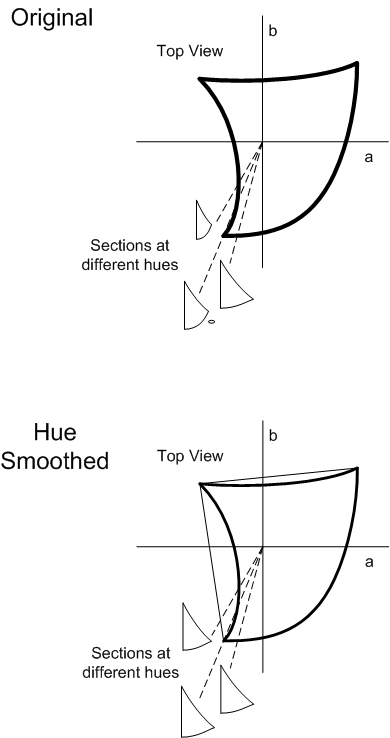
Abbildung 35 : Farbtonglättung
Ein Problem tritt bei Vorgängen auf, deren Farbton eingeschränkt ist. Das heißt, der Vorgang berücksichtigt nur Variablen innerhalb einer Farbtonebene. Abbildung 35 zeigt ein Beispiel für einen Gamut mit "diskontinuierlichen" Farbausschnitten in den blauen Farben. Innerhalb dieses Farbtonbereichs ist die Gamutgrenze für bestimmte Farbtonwinkel tangential zur Farbtonebene. In der Tat führt dies zu einer Änderung der topologischen Struktur der Farbtonscheiben. Im gezeigten Beispiel entsteht eine "Insel", während die Farbtonebene über diesen Farbtonbereich schweift und untertaucht. Diese Änderung in der Topologie führt dazu, dass farbspezifische Vorgänge nicht mehr reagiert werden. Beispielsweise ändert sich der Cusp bei festem Farbton abrupt, wenn sich der Farbtonwinkel in diesem Bereich ändert.
Es gibt einen farbwissenschaftlichen Grund, warum es wünschenswert ist, Farbton bei bestimmten Vorgängen beizubehalten. Um das vorherige Problem zu beheben, müssen die ursprünglichen Gamut-Begrenzungsdreiecke "Farbton geglättet" sein. Im Allgemeinen ist eine Farbtonglättung einer Reihe von Gamut-Begrenzungsdreiecken eine Reihe von Dreiecken, die (a) die Grenze eines neuen "Gamut" bildet, der möglicherweise nicht der tatsächlichen Geräteskala entspricht und den durch den ursprünglichen Satz von Dreiecken definierten Gamut enthält; und (b) die Dreiecke in der neuen Menge sind nicht parallel zu den Farbtonebenen begrenzt.
Eine praktische Möglichkeit, einen geglätteten Satz von Dreiecken zu erhalten, besteht darin, den konvexen Rumpf der ursprünglichen Scheitelpunkte zu nehmen. Wie in Abbildung 35 dargestellt, variieren die Farbtonscheiben des konvexen Rumpfs im problematischen Farbtonbereich problemlos, ohne dass sich die Topologie plötzlich ändert.
Festlegen von Primär- und Sekundärdateien in der Gamut-Begrenzungsbeschreibung
Bestimmte Methoden für die Gamutzuordnung, z. B. HueMap, hängen von der Position der Geräteprimare und sekundären Dateien ab. Bei additiven Geräten sind die Primaren rot, grün und blau (R, G und B); und die Sekundären sind Zyan, Magenta und Gelb (C, M und Y). Bei subtraktiven Geräten sind die Primärwerte C, M und Y; und die Sekundären sind R, G und B. Die GBD verfolgt alle sechs dieser Werte sowie Weiß und Schwarz (W und K) in einem Array von Jab-Farbwerten nach. Diese Werte werden in der Beschreibung der Gamutgrenze festgelegt, wenn sie erstellt wird. Für Ausgabegeräte können die Primärwerte bestimmt werden, indem Kombinationen von Gerätesteuerungswerten über das Gerätemodell ausgeführt werden. Für Erfassungsgeräte eignet sich dieser Ansatz nicht gut zum Erstellen der REFERENZ-GBD, da es fast unmöglich ist, ein Bild zu erfassen, das einen vollständig gesätten reinen Gerätewert ergibt, z. B. (0,0, 0,0, 1,0). WCS-Geräteprofile enthalten die Indizes der Primärwerte im Erfassungsziel. Da diese Werte nicht in einem ICC-Profil enthalten sind, verwenden Sie werte, die von einem typischen Scannerziel nach der Konvertierung in Jab gemessen werden, relativ zu den ICC-Anzeigebedingungen.
Festlegen der neutralen Achse in der Beschreibung der Gamut-Begrenzung
Die Methoden HueMap und relative MinCD-Gamutzuordnung verwenden die geräteneutrale Achse zum Richten. Für die Baselineausgabegeräte kann die neutrale Achse bestimmt werden, indem geräteneutrale Werte (R=G=B oder C=M=Y) über die DeviceToColorimetric-Methode und dann durch die ColorimetricToAppearance-Methode des CIECAM02-Objekts ausgeführt werden. Aufzeichnungsgeräte geben jedoch nicht immer einen geräteneutralen Wert zurück, wenn ein neutrales Beispiel angezeigt wird. Dies gilt insbesondere dann, wenn die Umgebungsbeleuchtung nicht vollkommen neutral ist. WCS-Geräteprofile enthalten die Indizes der neutralen Stichproben im Ziel. Verwenden Sie diese Beispiele, um die neutrale Achse festzulegen. Da diese Informationen für ICC-Profile nicht verfügbar sind, müssen Sie dieselbe Methode verwenden, die für Ausgabegeräte verwendet wird. Führen Sie geräteneutrale Beispiele über die DeviceToColorimetric-Methode aus, und koppeln Sie dann die Eingabewerte und die colorimetrischen Ergebnisse.
Zugehörige Themen