WCS-Farbgerätemodell: Profilschema und Algorithmen

Dieses Thema enthält Informationen zum WCS-Farbgerätemodellprofilschema und den zugehörigen Algorithmen.

Dieses Thema enthält folgende Abschnitte:

• Übersicht
• Architektur des Farbgerätemodellprofils
• Das CDMP-Schema
• WCS CDMP v2.0 Kalibrierungszugabe
• Die CDMP-Schemaelemente
  • ColorDeviceModelProfile
  • ColorDeviceModel
  • NamespaceVersion
  • Version
  • Dokumentation
  • CRTDevice-Element
  • LCDDevice-Element
  • ProjektorDevice-Element
  • ScannerDevice-Element
  • CameraDevice-Element
  • RGBPrinterDevice-Element
  • CMYKPrinterDevice-Element
  • RGBVirtualDevice-Element
  • PlugInDeviceType
  • RGBVirtualMeasurementType
  • GammaType
  • GammaOffsetGainType
  • GammaOffsetGainLinearGainType
  • ToneResponseCurvesType
  • GamutBoundarySamplesType
  • FloatPairList
  • CMYKPrinterMeasurementType
  • RGBPrinterMeasurementType
  • RGBCaptureMeasurementType
  • OneBasedIndex
  • RGBProjectorMeasurementType
  • DisplayMeasurementType
  • MeasurementConditionsType
  • GeometryType
  • RGBPrimariesGroup
  • NonNegativeCMYKSampleType
  • NonNegativeRGBSampleType
  • NonNegativeCMYKType
  • NonNegativeRGBType
  • ExtensionType
  • NonNegativeXYZType
  • XYZType
• CdMP-Baselinealgorithmen
  • CRT-Gerätemodellbaseline
  • Baseline des LCD-Gerätemodells
  • Baseline des RGB-Druckergerätemodells
  • Baseline des RGB-Modells für virtuelle Geräte
  • CMYK-Druckergerätemodellbaseline
  • RGB-Projektor–Gerätemodellbaseline
  • ICC-Gerätemodellbaseline
• Zugehörige Themen

Übersicht

Dieses Schema wird verwendet, um den Inhalt eines Farbgerätemodellprofils (CDMP) anzugeben. Die zugehörigen Baselinealgorithmen werden unten beschrieben.

Das DMP-Schema (Basic Device Model Profile) besteht aus den Stichprobenmessdaten.

Die Samplingkomponente des DMP-XML-Schemas bietet Unterstützung für grundlegende Farbmessungsziele und konzentriert sich dabei auf allgemeine Standardziele und Ziele, die für die Basisgerätemodelle optimiert sind.

Darüber hinaus stellt das Geräteprofil spezifische Informationen zum Zielgerätemodell bereit und stellt eine Richtlinie bereit, die das geplante Fallbackgerätemodell verwenden kann, wenn das Zielmodell nicht verfügbar ist. Die Profilinstanzen können private Erweiterungen mithilfe von XML-Standarderweiterungsmechanismen enthalten.

Architektur des Farbgerätemodellprofils

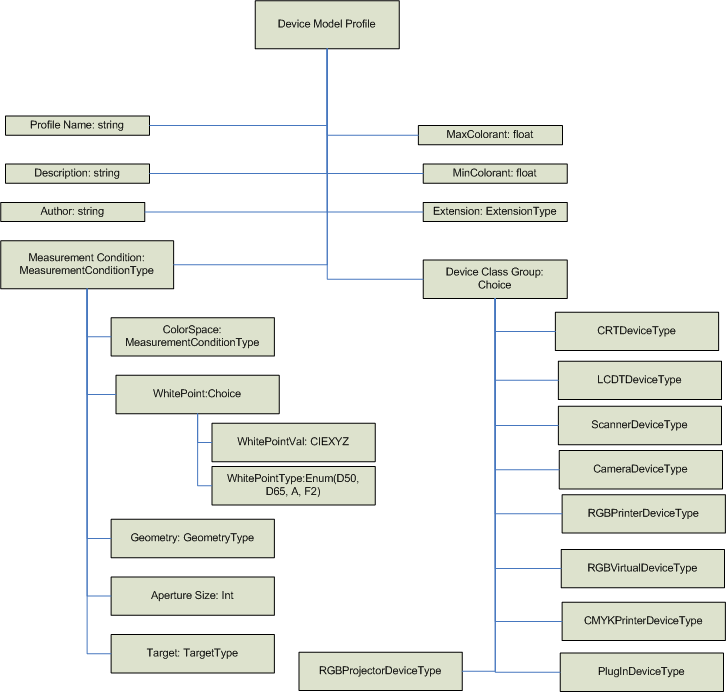
Das CDMP-Schema

<?xml version="1.0" encoding="UTF-8"?>
<xs:schema 
  xmlns:cdm="http://schemas.microsoft.com/windows/2005/02/color/ColorDeviceModel"
  xmlns:wcs="http://schemas.microsoft.com/windows/2005/02/color/WcsCommonProfileTypes"
  targetNamespace="http://schemas.microsoft.com/windows/2005/02/color/ColorDeviceModel"
  xmlns:xs="http://www.w3.org/2001/XMLSchema"
  elementFormDefault="qualified"
  attributeFormDefault="unqualified"
  blockDefault="#all"
  version="1.0">

  <xs:annotation>
    <xs:documentation>
      Color Device Model profile schema.
      Copyright (C) Microsoft. All rights reserved.
    </xs:documentation>
  </xs:annotation>

  <xs:import namespace="http://schemas.microsoft.com/windows/2005/02/color/WcsCommonProfileTypes" />

  <xs:complexType name="RGBType">
    <xs:attribute name="R" type="xs:float" use="required"/>
    <xs:attribute name="G" type="xs:float" use="required"/>
    <xs:attribute name="B" type="xs:float" use="required"/>
  </xs:complexType>

  <xs:complexType name="NonNegativeRGBType">
    <xs:attribute name="R" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="G" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="B" type="wcs:NonNegativeFloatType" use="required"/>
  </xs:complexType>

  <xs:complexType name="NonNegativeCMYKType">
    <xs:attribute name="C" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="M" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="Y" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="K" type="wcs:NonNegativeFloatType" use="required"/>
  </xs:complexType>
  
  <xs:complexType name="NonNegativeRGBSampleType">
    <xs:sequence>
      <xs:element name="RGB" type="cdm:NonNegativeRGBType"/>
      <xs:element name="CIEXYZ" type="wcs:NonNegativeCIEXYZType"/>
    </xs:sequence>
    <xs:attribute name="Tag" type="xs:string" use="optional"/>
  </xs:complexType>
  
  <xs:complexType name="NonNegativeCMYKSampleType">
    <xs:sequence>
      <xs:element name="CMYK" type="cdm:NonNegativeCMYKType"/>
      <xs:element name="CIEXYZ" type="wcs:NonNegativeCIEXYZType"/>
    </xs:sequence>
    <xs:attribute name="Tag" type="xs:string" use="optional"/>
  </xs:complexType>
  
  <xs:group name="RGBPrimariesGroup">
    <xs:sequence>
      <xs:element name="WhitePrimary" type="wcs:NonNegativeCIEXYZType"/>
      <xs:element name="RedPrimary" type="wcs:NonNegativeCIEXYZType"/>
      <xs:element name="GreenPrimary" type="wcs:NonNegativeCIEXYZType"/>
      <xs:element name="BluePrimary" type="wcs:NonNegativeCIEXYZType"/>
      <xs:element name="BlackPrimary" type="wcs:NonNegativeCIEXYZType"/>
    </xs:sequence>
  </xs:group> 
  
  <xs:complexType name="MeasurementConditionsType">
    <xs:annotation>
      <xs:documentation>
      Optional measurement conditions. 
       
      We only support CIEXYZ for measurement color space in this version. 
      If the white point value from the measurement conditions is not available, 
      the default processing will use
        - "D50" for printer and scanners
        - "D65" for camera and displays.          
      </xs:documentation>
    </xs:annotation>
    <xs:sequence>
      <xs:element name="ColorSpace" minOccurs="0">
        <xs:simpleType>
          <xs:restriction base="xs:string">
            <xs:enumeration value="CIEXYZ"/>
          </xs:restriction>
        </xs:simpleType>    
      </xs:element>
      <xs:choice minOccurs="0">
        <xs:element name="WhitePoint" type="wcs:NonNegativeCIEXYZType"/>
        <xs:element name="WhitePointName">
          <xs:simpleType>
            <xs:restriction base="xs:string">
              <xs:enumeration value="D50"/>
              <xs:enumeration value="D65"/>
              <xs:enumeration value="A"/>
              <xs:enumeration value="F2"/>
            </xs:restriction>
          </xs:simpleType>
        </xs:element>
      </xs:choice>
      <xs:element name="Geometry" minOccurs="0">
        <xs:simpleType>
          <xs:restriction base="xs:string">
            <xs:enumeration value="0/45"/>
            <xs:enumeration value="0/diffuse"/>
            <xs:enumeration value="diffuse/0"/>
            <xs:enumeration value="direct"/>
          </xs:restriction>
        </xs:simpleType>   
      </xs:element>
      <xs:element name="ApertureSize" type="xs:int" minOccurs="0"/>
    </xs:sequence>
  </xs:complexType>
  
  <xs:complexType name="DisplayMeasurementType">
    <xs:sequence>
      <xs:group ref="cdm:RGBPrimariesGroup"/>
      <xs:element name="GrayRamp">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="4096"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>
      <xs:element name="RedRamp">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="4096"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>
      <xs:element name="GreenRamp">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="4096"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>
      <xs:element name="BlueRamp">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="4096"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>
    </xs:sequence>
    <xs:attribute name="TimeStamp" type="xs:dateTime"/>
  </xs:complexType>

  <xs:complexType name="RGBProjectorMeasurementType">
    <xs:sequence>
      <xs:group ref="cdm:RGBPrimariesGroup"/>
      <xs:element name="ColorSamples">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="unbounded"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>
    </xs:sequence>
    <xs:attribute name="TimeStamp" type="xs:dateTime"/>
  </xs:complexType>

  <xs:simpleType name="OneBasedIndex">
    <xs:restriction base="xs:int">
      <xs:minInclusive value="1"/>
    </xs:restriction>
  </xs:simpleType>
    
  <xs:complexType name="RGBCaptureMeasurementType">
    <xs:sequence>
      <xs:element name="PrimaryIndex">
        <xs:complexType>
          <xs:all>
            <xs:element name="White" type="cdm:OneBasedIndex"/>
            <xs:element name="Black" type="cdm:OneBasedIndex" minOccurs="0"/>
            <xs:element name="Red" type="cdm:OneBasedIndex" minOccurs="0"/>
            <xs:element name="Green" type="cdm:OneBasedIndex" minOccurs="0"/>
            <xs:element name="Blue" type="cdm:OneBasedIndex" minOccurs="0"/>
            <xs:element name="Cyan" type="cdm:OneBasedIndex" minOccurs="0"/>
            <xs:element name="Magenta" type="cdm:OneBasedIndex" minOccurs="0"/>
            <xs:element name="Yellow" type="cdm:OneBasedIndex" minOccurs="0"/>
          </xs:all>
        </xs:complexType>
      </xs:element>
      <xs:element name="NeutralIndices">
        <xs:simpleType>
          <xs:list itemType="cdm:OneBasedIndex"/>
        </xs:simpleType>
      </xs:element>
      <xs:element name="ColorSamples">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="unbounded"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>
    </xs:sequence>
    <xs:attribute name="TimeStamp" type="xs:dateTime"/>
  </xs:complexType>

  <xs:complexType name="RGBPrinterMeasurementType">
    <xs:sequence>
      <xs:element name="ColorCube">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="unbounded"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>       
    </xs:sequence>
    <xs:attribute name="TimeStamp" type="xs:dateTime"/>
  </xs:complexType>
  
  <xs:complexType name="CMYKPrinterMeasurementType">
    <xs:sequence>
      <xs:element name="ColorCube">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeCMYKSampleType" maxOccurs="unbounded"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>       
    </xs:sequence>
    <xs:attribute name="TimeStamp" type="xs:dateTime"/>
  </xs:complexType>

  <xs:complexType name="GammaType">
    <xs:attribute name="value" type="wcs:NonNegativeFloatType" use="required"/>
  </xs:complexType>
  
  <xs:complexType name="GammaOffsetGainType">
    <xs:attribute name="Gamma" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="Offset" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="Gain" type="wcs:NonNegativeFloatType" use="required"/>
  </xs:complexType>

  <xs:complexType name="GammaOffsetGainLinearGainType">
    <xs:attribute name="Gamma" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="Offset" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="Gain" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="LinearGain" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="TransitionPoint" type="wcs:NonNegativeFloatType" use="required"/>
  </xs:complexType>
  
  <xs:simpleType name="FloatList">
    <xs:list itemType="xs:float"/>
  </xs:simpleType>

  <xs:complexType name="OneDimensionLutType">
    <xs:sequence>
      <xs:element name="Input" type="cdm:FloatList"/>
      <xs:element name="Output" type="cdm:FloatList"/>
    </xs:sequence>
  </xs:complexType>

  <xs:complexType name="HDRToneResponseCurvesType">
    <xs:sequence>
      <xs:element name="RedTRC" type="cdm:OneDimensionLutType"/>
      <xs:element name="GreenTRC" type="cdm:OneDimensionLutType"/>
      <xs:element name="BlueTRC" type="cdm:OneDimensionLutType"/>
    </xs:sequence>
    <xs:attribute name="TRCLength" use="required">
      <xs:simpleType>
        <xs:restriction base="xs:int">
          <xs:minInclusive value="0" />
        </xs:restriction>
      </xs:simpleType>
    </xs:attribute>
  </xs:complexType>
  
  <xs:complexType name="GamutBoundarySamplesType">
    <xs:sequence>
      <xs:element name="RGB" type="cdm:RGBType" maxOccurs="unbounded"/>
    </xs:sequence>
  </xs:complexType>
  
  <xs:complexType name="RGBVirtualMeasurementType">
    <xs:sequence>
      <xs:element name="MaxColorantUsed" type="xs:float"/>
      <xs:element name="MinColorantUsed" type="xs:float"/>
      <xs:group ref="cdm:RGBPrimariesGroup"/>
      <xs:choice>
        <xs:element name="Gamma" type="cdm:GammaType"/>
        <xs:element name="GammaOffsetGain" type="cdm:GammaOffsetGainType"/>
        <xs:element name="GammaOffsetGainLinearGain" type="cdm:GammaOffsetGainLinearGainType"/>
        <xs:element name="HDRToneResponseCurves" type="cdm:HDRToneResponseCurvesType"/>
      </xs:choice>
      <xs:element name="GamutBoundarySamples" type="cdm:GamutBoundarySamplesType" minOccurs="0"/>
    </xs:sequence>
    <xs:attribute name="TimeStamp" type="xs:dateTime"/>
  </xs:complexType>
  
  <xs:element name="ColorDeviceModel">
    <xs:complexType>
      <xs:sequence>
        <xs:element name="ProfileName" type="wcs:MultiLocalizedTextType"/>
        <xs:element name="Description" type="wcs:MultiLocalizedTextType" minOccurs="0"/>
        <xs:element name="Author" type="wcs:MultiLocalizedTextType" minOccurs="0"/>
        <xs:element name="MeasurementConditions" type="cdm:MeasurementConditionsType" minOccurs="0"/>
        <xs:element name="SelfLuminous" type="xs:boolean" />
        <xs:element name="MaxColorant" type="xs:float"/>
        <xs:element name="MinColorant" type="xs:float"/>
        <xs:choice>
          <xs:element name="CRTDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:DisplayMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="LCDDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:DisplayMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="RGBProjectorDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:RGBProjectorMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="ScannerDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:RGBCaptureMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="CameraDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:RGBCaptureMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="RGBPrinterDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:RGBPrinterMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="CMYKPrinterDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:CMYKPrinterMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="RGBVirtualDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:RGBVirtualMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
        </xs:choice>
        <xs:element name="PlugInDevice" minOccurs="0">
          <xs:complexType>
            <xs:sequence>
              <xs:any namespace="##other" processContents="skip"
                minOccurs="0" maxOccurs="unbounded" />
            </xs:sequence>
            <xs:attribute name="GUID" type="wcs:GUIDType" use="required"/>
          </xs:complexType>
        </xs:element>
      </xs:sequence>
      <xs:attribute name="ID" type="xs:string" use="optional" />
    </xs:complexType>
  </xs:element>
</xs:schema>

WCS CDMP v2.0 Kalibrierungszugabe

Das ColorDeviceModel-Element des CDMP-Schemas wurde in Windows 7 aktualisiert, um das neue Kalibrierungselement einzuschließen. Im Folgenden wird die Änderung des CDMP-Schemas veranschaulicht.

  ...
  <xs:element name="ColorDeviceModel">
    <xs:complexType>
      <xs:sequence>
        ...
        <xs:element name="PlugInDevice" minOccurs="0">
             ...
        </xs:element>
        <xs:element name="Calibration" type="cal:Calibration" minOccurs="0"/>
        ...
      <xs:sequence>
    ...
    <xs:complexType>
  ...

Die CDMP-Schemaelemente

Hinweis

Vorwahlen sind Primärbeispiele von Rot, Grün, Blau, Schwarz und Weiß. Eine primäre Rampe ist eine tonale Rampe von der geringsten Leuchtdichte bis zum vollständigen primären Wert. Die maximale Anzahl von Einträgen in einer Tonrampe ist 4096.

Hinweis

DMPs sind erforderlich, um Über Messdaten zu verfügen.

ColorDeviceModelProfile

Dieses Element ist vom Typ ColorDeviceModel.

Validierungsbedingungen: Jedes Unterelement wird durch einen eigenen Typ überprüft.

ColorDeviceModel

Dieses Element ist eine Sequenz der folgenden Unterelemente

1. ProfileName-Zeichenfolge,
2. optionale Beschreibungszeichenfolge,
3. optionale Author-Zeichenfolge,
4. optional MeasurementConditions MeasurementConditionsType,
5. Self-Luminous Boolean,
6. MaxColorant float,
7. MinColorant float,
8. Auswahl der Elemente
   1. CRTDevice,
   2. LCDDevice,
   3. RGBProjectorDevice,
   4. ScannerDevice,
   5. CameraDevice,
   6. RGBPrinterDevice,
   7. CMYKPrinterDevice,
   8. RGBVirtualDevice,
9. PlugInDevice,
10. Optionaler ExtensionType-Erweiterungstyp

Validierungsbedingungen: Jedes Unterelement wird durch einen eigenen Typ überprüft. Zeichenfolgenunterelemente haben maximal 10.000 Zeichen. Das MaxColorant-Unterelement muss größer oder gleich 0 (0) und größer als das MinColorant-Unterelement sein. MinColorant kann negativ sein.

NamespaceVersion

xmlns:cdm="http://schemas.microsoft.com/windows/2005/02/color/ColorDeviceModel"

targetNamespace="http://schemas.microsoft.com/windows/2005/02/color/ColorDeviceModel"

Version

Version = "1.0" mit Windows Vista.

Validierungsbedingungen: Jeder Versionswert >0.1 oder <=2.0 ist gültig, um unterbrechungsfreie Änderungen am Format zu unterstützen.

Dokumentation

Schema des Gerätemodellprofils.

Copyright (C) Microsoft. Alle Rechte vorbehalten.

CRTDevice-Element

Dieses Element ist eine Sequenz von Unterelementen eines MeasurementData DisplayMeasurementType.This element is a sequence of sub-elements of a MeasurementData DisplayMeasurementType.

Validierungsbedingungen: Jedes Unterelement wird durch einen eigenen Typ überprüft.

LCDDevice-Element

Dieses Element ist eine Sequenz von Unterelementen eines MeasurementData DisplayMeasurementType.This element is a sequence of sub-elements of a MeasurementData DisplayMeasurementType.

Validierungsbedingungen: Jedes Unterelement wird durch einen eigenen Typ überprüft.

ProjectorDevice-Element

Dieses Element ist eine Sequenz von Unterelementen eines MeasurementData RGBProjectorMeasurementType.

Validierungsbedingungen: Jedes Unterelement wird durch einen eigenen Typ überprüft.

ScannerDevice-Element

Dieses Element ist eine Sequenz von Unterelementen eines MeasurementData RGBCaptureMeasurementType

Validierungsbedingungen: Jedes Unterelement wird durch einen eigenen Typ überprüft.

CameraDevice-Element

Dieses Element ist eine Sequenz von Unterelementen eines MeasurementData RGBCaptureMeasurementType

Validierungsbedingungen: Jedes Unterelement wird durch einen eigenen Typ überprüft.

RGBPrinterDevice-Element

Dieses Element ist eine Sequenz von Unterelementen eines MeasurementData RGBPrinterMeasurementType.This element is a sequence of sub-elements of a MeasurementData RGBPrinterMeasurementType.

Validierungsbedingungen: Jedes Unterelement wird durch einen eigenen Typ überprüft.

CMYKPrinterDevice-Element

Dieses Element ist eine Sequenz von Unterelementen eines MeasurementData CMYKPrinterMeasurementType.This element is a sequence of sub-elements of a MeasurementData CMYKPrinterMeasurementType.

Validierungsbedingungen: Jedes Unterelement wird durch einen eigenen Typ überprüft.

RGBVirtualDevice-Element

Dieses Element ist eine Sequenz von Unterelementen eines RGBVirtualMeasurementDataType.This element is a sequence of sub-elements of a RGBVirtualMeasurementDataType.

Validierungsbedingungen: Jedes Unterelement wird durch einen eigenen Typ überprüft.

PlugInDeviceType

Dieses Element ist eine Sequenz eines GUID-GUIDTypes und beliebiger Unterelemente.

Validierungsbedingungen: Die GUID wird verwendet, um die DM PlugIn Dll-GUID abzugleichen. Es gibt maximal 100.000 benutzerdefinierte Unterelemente.

RGBVirtualMeasurementType

Dieses Element ist eine Sequenz, die aus

1. RGBPrimariesGroup-Gruppe

2. Eine Auswahl von

3. • Gamma
   • GammaOffsetGain
   • GammaOffsetGainLinearGam
   • ToneResponseCurves-Elemente

4. optional GamutBoundarySamples GamutBoundarySamplesType

5. TimeStamp dateTime

Validierungsbedingungen: Jedes Unterelement dieser Typen verfügt über eigene Validierungsbedingungen.

GammaType

Dieses Element ist ein komplexer Typ, der aus dem -Attribut besteht.

• Gamma NonNegativeFloatType

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

GammaOffsetGainType

Dieses Element ist ein komplexer Typ, der aus den Attributen besteht.

• Gamma NonNegativeFloatType
• Offset NonNegativeFloatType
• Gain NonNegativeFloatType

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

GammaOffsetGainLinearGainType

Dieses Element ist ein komplexer Typ, der aus den Attributen besteht.

• Gamma NonNegativeFloatType
• Offset NonNegativeFloatType
• Gain NonNegativeFloatType
• LinearGain NonNegativeFloatType
• TransitionPoint NonNegativeFloatType.

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

ToneResponseCurvesType

Dieses Element ist eine Sequenz von

1. RedTRC FloatPairList
2. GreenTRC FloatPairList
3. BlueTRC FloatPairList

Das Element verfügt außerdem über ein TRCLength-Attribut vom Typ unsignedint.

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

GamutBoundarySamplesType

Dieses Element ist eine Sequenz von RGB RGBTypes.

Validierungsbedingungen: Derzeit gibt es unbegrenzte Höchstwerte, die basierend auf Branchenfeedback begrenzt werden sollen.

FloatPairList

Dieses Element ist ein einfacher Typ von Listenpaaren von Floats.

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

CMYKPrinterMeasurementType

Dieses Element ist ein

1. Sequenz des ColorCube-Elements, bestehend aus einer Sequenz von Sample NonNegativeCMYKSampleType

2. TimeStamp dateTime-Attribut.

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

RGBPrinterMeasurementType

Dieses Element ist ein

1. Sequenz des ColorCube-Elements, bestehend aus einer Sequenz von Sample NonNegativeRGBSampleType

2. TimeStamp dateTime-Attribut.

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

RGBCaptureMeasurementType

Dieses Element ist eine Sequenz von

1. PrimaryIndex complexType von

2. 1. Weißer OneBasedIndex
   2. Optionaler Schwarzer OneBasedIndex
   3. Optionaler Roter OneBasedIndex
   4. Optionaler grüner OneBasedIndex
   5. Optionaler blauer OneBasedIndex
   6. Optionaler Cyan OneBasedIndex
   7. Optionaler Magenta OneBasedIndex
   8. Optionaler gelber OneBasedIndex

3. NeutralIndices von OneBasedIndex-Zeilen

4. ColorSamples-Sequenz von Sample NonNegativeRGBSampleType

Das Element verfügt außerdem über ein DateTime-Attribut timeStamp.

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

OneBasedIndex

Dieses Element ist ein einfacher Typ von Einschränkungsbasis ohne Vorzeichen mit minInclusive value = "1".

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

RGBProjectorMeasurementType

Dieses Element ist eine Sequenz von

1. RGBPrimariesGroup-Gruppe
2. Element ColorSamples, bestehend aus einer Sequenz von Sample NonNegativeRGBSampleType

Das Element verfügt außerdem über ein DateTime-Attribut timeStamp.

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

DisplayMeasurementType

Dieses Element ist eine Sequenz von

1. group RGBPrimariesGroup
2. GrayRamp der Sequenz von Sample NonNegativeRGBType
3. RedRamp der Sequenz von Sample NonNegativeRGBType
4. GreenRamp der Sequenz des Beispiels NonNegativeRGBType
5. BlueRamp der Sequenz von Sample NonNegativeRGBType

Das DisplayMeasurementType-Element verfügt außerdem über das DateTime-Attribut TimeStamp.

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

MeasurementConditionsType

MeasurementConditionsType ist eine Sequenz von Unterelementen, die Folgendes enthält:

1. ColorSpace: Eingeschränkter Zeichenfolgenenumerationswert von "CIEXYZ"
2. optionale Auswahl der WhitePoint NonNegativeXYZType- oder WhitePointName-Zeichenfolgenenumeration von Werten D50, D65, A oder F2
3. Geometry GeometryType
4. ApertureSize integer in Millimetern

Standardwerte sind:

1. RGB- und CMYK-Drucker:
   1. CIEXYZ MeasurementSpaceType
   2. D50 WhitePointValue
   3. 0/45 GeometryType
   4. 10mm ApertureSize
2. Scanner:
   1. CIEXYZ MeasurementSpaceType
   2. D50 WhitePointValue
   3. 0/45 GeometryType
   4. 10mm ApertureSize
3. Anzeigen und virtuelles RGB-Gerät:
   1. CIEXYZ MeasurementSpaceType
   2. D65 WhitePointValue
   3. 0/45 GeometryType
   4. 10mm ApertureSize
4. Kameras:
   1. CIEXYZ MeasurementSpaceType
   2. D65 WhitePointValue
   3. Direct GeometryType
   4. 10mm ApertureSize

Validierungsbedingungen: Die Validierung jedes Unterelements wird durch Validierungsbedingungen für diese Unterelemente bestimmt. Wenn ein Unterelement fehlt, wird der standardspezifische Gerätemodelltyp verwendet.

GeometryType

String

Enumerationswerte:

• "0/45"
• "0/diffus"
• "diffus/0"
• "Direkt"

Validierungsbedingungen: Alle Werte außer den aufgeführten Zahlenwerten sind ungültig. Diese Informationen ändern das Grundlegendeverarbeitungsverhalten nicht.

RGBPrimariesGroup

Dieses Element ist eine Sequenz von

1. WhitePrimary NonNegativeXYZType
2. RedPrimary NonNegativeXYZType
3. GreenPrimary NonNegativeXYZType
4. BluePrimary NonNegativeXYZTYpe
5. BlackPrimary NonNegativeXYZType

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

NonNegativeCMYKSampleType

Dieses Element ist eine Sequenz von

1. CMYK NonNegativeCMYKType
2. CIEXYZ NonNegativeXYZType

Das Element verfügt auch über eine optionale Attribut-Tagzeichenfolge.

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

NonNegativeRGBSampleType

Dieses Element ist eine Sequenz von

1. RGB NonNegativeRGBType
2. CIEXYZ NonNegativeXYZType

Das Element verfügt auch über eine optionale Attribut-Tagzeichenfolge.

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

NonNegativeCMYKType

Dieses Element besteht aus Attributen

1. C float
2. M float
3. Y float
4. K float

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

NonNegativeRGBType

Dieses Element besteht aus Attributen

1. R Float
2. G float
3. B float

Validierungsbedingungen: Anhand des Branchenfeedbacks ermittelt werden.

ExtensionType

Das ExtensionType-Element ist eine Sequenz eines beliebigen Unterelementtyps und wird für proprietäre Informationen von Nicht-Microsoft-Anwendungen verwendet.

Validierungsbedingungen: Dieses Element ist optional. Es können maximal 1.000 Erweiterungsunterelemente vorhanden sein.

NonNegativeXYZType

Das NonNegativeXYZType-Element besteht aus nonNegativeFloatType drei IEEE-Gleitkommaelementen mit einfacher Genauigkeit namens "X", "Y" und "Z". Diese Werte sind auf die DMP-Profile-Messwerte beschränkt. Diese Messungen können entweder absolute (nicht relative) CIEXYZ 1931 reflektierende Werte oder absolute (nicht relative) CIEXYZ 1931 direkte (transmissive) Werte in Candelas pro Quadrateinheit sein.

Validierungsbedingungen: Nur reale Werte sind gültig, und negative CIEXYZ-Messwerte sind ungültig. Da es sich um absolute Werte handelt, können Werte größer als 1,0f sein. Ein angemessener Grenzwert für jeden "X"-, "Y"- oder "Z."-Wert wird willkürlich auf 10000,0f festgelegt.

XYZType

Das XYZType-Element besteht aus drei IEEE-Gleitkommawerten mit einfacher Genauigkeit: "X", "Y" und "Z".

Die CDMP-Baselinealgorithmen

CRT-Gerätemodellbaseline

Um dieses Modell zu verstehen, müssen Sie sowohl den Charakterisierungsprozess als auch die Gerätemodellierung berücksichtigen. Bei der Charakterisierung werden zunächst XYZ-Messungen an den Farben durchgeführt, die durch Auffüllen des Anzeigepuffers eines CRT-Anzeigegeräts erhalten werden. Die folgenden Beispielwerte generieren gute Daten für das geplante CRT-Gerätemodell:

Rot: R = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, G = B = 0

Grün: G = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, R = B = 0

Blau: B = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, R = G = 0

Neutrale: R = G= B = 0, 8, 16, 32, 64, 128, 192, 255

Es können auch andere Inkremente als 15 und nichtlineare Inkremente verwendet werden. Jede rote, grüne, blaue und neutrale Rampe muss mindestens drei Proben enthalten, aber es wird empfohlen, weitere Proben bereitzustellen. Sie müssen Beispiele für reines Rot, Grün, Blau, Schwarz und Weiß bereitstellen. Die Beispiele müssen nicht einheitlich angeordnet sein.

Der Prozess der Erstellung der Tristimulusmatrix besteht aus zwei Schritten. Schätzen Sie zunächst den XYZ-Wert des schwarzen Punkts oder die Flare. Dieser Schritt basiert größtenteils auf der Arbeit von Berns[3] mit einer leicht modifizierten Objective-Funktion für die nichtlineare Optimierung. Zweitens berechnen Sie die Tristimulusmatrix basierend auf dem Ergebnis aus Schritt 1 und auch aus einer Durchschnittsberechnung für alle Messungen pro Kanal, nicht nur die für die maximale digitale Anzahl.

Jeder dieser Schritte enthält detaillierte Verfahren. Der Ausgangspunkt sind die Rampen (in unserem Beispiel 17 Schritte) für jeden R-, G- und B-Kanal. Wenn die XYZ-Messungen auf der Chromatik xy-Ebene gezeichnet werden, wird in Abbildung 1 eine typische Situation dargestellt. Schritt 1 besteht darin, ein nichtlineares Optimierungsproblem zu lösen, um den "am besten geeigneten" Schwarzen Punkt zu finden, der die Drift in der Chromität minimiert, während man die R-, G- und B-Kanäle durchläuft. Basierend auf Berns[3] suchen wir nach ( X_K,YK,ZK ), das die folgende objektive Funktion minimiert:

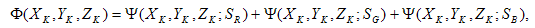
Dabei sind S_R, S_G und S_B der Satz von Datenpunkten, die den Punkten auf den R-, G- und B-Kanälen entsprechen. Definieren Sie für jede Menge S Folgendes:

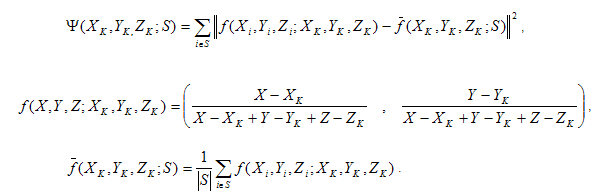
Oben wird | S | ist die Kardinalität von S, d.h. die Anzahl der Punkte im Satz S. 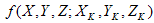ist die Chromitätkoordinate des Punkts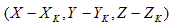 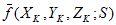, ist der Mittelwert oder der Massenmittelpunkt aller Punkte in der Gruppe S in der Chromitätsebene. Zeigt also 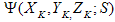ist die Summe der zweiten Momente der Punkte über den Massenmittelpunkt und ist ein Maß dafür, wie verteilt die Punkte darüber sind. 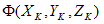ist ein Gesamtmaß dafür, wie verteilt sich die drei Punktcluster über ihre jeweiligen Massenzentren befinden.

In der Berechnung von 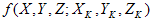, wenn 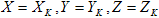wird die Berechnung übersprungen, und die Kardinalität von S wird entsprechend angepasst.

Trotz der scheinbaren Komplexität der Objektivfunktion ist sie eine Summe der Quadrate vieler differenzierbarer Funktionen in X_{K,YKZ K} (17 Punkte 2xy -komponenten 3 Kanäle = 102, im Beispiel), und ist daher für Standardtechniken der nichtlinearen kleinsten Quadrate wie dem Levenberg-Marquardt-Algorithmus, der in WCS verwendet wird, verfügbar. Beachten Sie, dass sich die vorangehende Zielfunktion von der in Berns[3] vorgeschlagenen unterscheidet, da die letztere Funktion die Varianz der Entfernungen vom Massenmittelpunkt misst, sodass die Varianz null ist, wenn die Punkte vom Massenmittelpunkt gleich sind, auch wenn sie sich darüber ziemlich ausbreiten können. Im Beispiel wird die Verteilung der Punkte direkt mithilfe der zweiten Momente konvergiert.

Wie bei jedem iterativen Algorithmus für das Problem der nichtlinearen kleinsten Quadrate erfordert Levenberg-Marquardt eine erste Schätzung. Es gibt zwei offensichtliche Kandidaten. Einer ist (0, 0, 0); die andere ist der gemessene Schwarze Punkt. Für die CTE wird zuerst der gemessene Schwarze Punkt als erste Schätzung verwendet. Wenn maximal 100 Iterationen überschritten werden, ohne einen Schwellenwert von einem durchschnittlichen Abstand von 0,001 von jedem Punkt von seinem Massenmittelpunkt zu erreichen (was einem Schwellenwert von (0,001) 17 3 = 0,000051 für die Zielfunktion entspricht), wird eine weitere Iterationsrunde mit der anfänglichen Schätzung von (0, 0, 0) durchgeführt. Die resultierende Schätzung des Schwarzen Punkts ist XYZ im Vergleich mit der besten Schätzung aus der vorherigen Iterationsrunde (mit dem gemessenen schwarzen Punkt als anfängliche Schätzung). Verwenden Sie die Schätzung, die den kleinsten Wert für die Objective-Funktion angibt. Die Auswahl von 100 Iterationen und der Fehlerabstand von 0,001 wurden jeweils empirisch ausgewählt. In zukünftigen Versionen kann es sinnvoll sein, den Fehlerabstand zu parametrisieren.

Das Ergebnis von Schritt 1 ist der geschätzte Schwarze Punkt ( X_K,YK,ZK ). Schritt 2 besteht darin, die Tristimulusmatrix zu bestimmen, indem die Chromizität der Punkte in den drei Clustern, die in Schritt 1 ermittelt wurden, ergibt. Bei CRTs erfolgt dies in erster Linie, um die Auswirkungen von Messfehlern zu minimieren. Die punkte, die bei der Chromitätsverwertung verwendet werden, müssen dieselben Punkte sein, die in der Optimierung in Schritt 1 verwendet wurden. Anders ausgedrückt: Wenn der erste Punkt (digitale Anzahl 15, im Beispiel) in jeder Rampe im Optimierungsschritt verworfen wird, muss dasselbe in der Mittelung erfolgen. Wenn 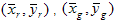und 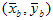sind die gemittelten Farbigkeitskoordinaten der roten, grünen und blauen Kanäle, dann bestimmt das folgende Verfahren die Tristimulusmatrix. Lösen Sie zunächst das lineare 3?3-System:

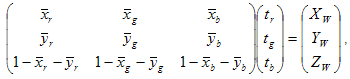
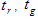
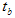
X_W, Y_W, Z_W

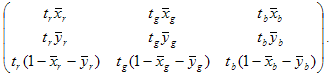
Nachdem die Tristimulusmatrix bestimmt wurde, folgt die Bestimmung der Tonkurven dem Standardansatz. Bei CRT-Anzeigen wird davon ausgegangen, dass die einzelnen Kanäle dem "GOG"-Modell folgen:

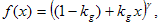
wobei k_g der "Gain", 1 -k_g der "Offset" und ? ist das "Gamma". Die umgekehrte Matrix der Tristimulusmatrix wird auf die XYZ-Daten der Neutralen angewendet, um die linearen RGB-Daten zu erhalten, die dann mithilfe der nichtlinearen Regression im GOG-Modell mit den digitalen RGB-Werten korreliert werden. Diese Eigenschaften müssen für die R-, G- und B-Kanäle nicht identisch sein und sind im Allgemeinen nicht identisch.

Berns[1]: Berns, Billmeyer und Saltzmans Prinzipien der Farbtechnologie, 3 _rd Ed. John Wiley & Sons (2000).

Berns[2]: Berns und Katoh, Die digital-radiometrische Übertragungsfunktion für computergesteuerte CRT-Displays, CIE Expert Symposium '97 Color Standards for Imaging Technology, Nov. 1997.

Berns[3]: Berns, Fernandez und Taplin, Schätzung Black-Level Emissionen von Computer-Controlled Displays, Farbforschung und Anwendung, 28: 379-383 Wiley Periodicals, Inc. (2003)

Kang[1]: Kang, Color Technology for Electronic Imaging Devices, SPIE (1997)

Katoh[1]: Katoh, Deguchi und Berns, Eine genaue Charakterisierung des CRT-Monitors (II) Vorschlag für eine Erweiterung der CIE-Methode und deren Überprüfung, Opt. Rev. 8: 397-408 (2001)

Baseline des LCD-Gerätemodells

Die Baseline des LCD-Gerätemodells ähnelt der CRT-Gerätemodellbaseline. In diesem Abschnitt wird erläutert, wie sich die LCD-Modellierung von der CRT-Modellierung unterscheidet.

Ein Unterschied besteht darin, dass Sie nicht davon ausgehen können, dass LCD-Displays dem für CRTs verwendeten GOG-Modell folgen und die Tonkurven durch Interpolation der gemessenen Daten abgerufen werden. Aus diesem Gründen sollte die geräteneutrale Achse häufiger abgetastet werden.

Im Folgenden finden Sie einige typische Beispielwerte, die gute Daten für die Baseline des LCD-Gerätemodells generieren können:

Rot: R = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, G = B = 0

Grün: G = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, R = B = 0

Blau: B = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, R = G = 0

Neutrale: R = G = B = 0, 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255.

Der Prozess der averagierenden gemessenen Farbchromaten, um die Chromität für die Geräteprimries zu erhalten, ist für LCDs wichtiger als für CRTs. Wenn XYZ-Messungen auf der Chromität xy-Ebene gezeichnet werden, wird in Abbildung 1 eine typische Situation dargestellt. Beachten Sie, wie die Chromität in Richtung des Schwarzen Punkts driftet. Dies liegt daran, dass alle LCDs eine bestimmte Menge an Lichtlecks aufweisen.

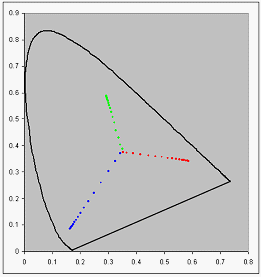
Abbildung 1 : Das Chromitätsdiagramm unter Verwendung von Rohdaten ohne Korrektur

Wenn dies von den rohen XYZ-Messungen subtrahiert wird, wird in Abbildung 2 eine typische Situation dargestellt. Die Punkte sind jetzt um drei Zentren gruppiert, obwohl sie nicht identisch auf sie fallen. Der für CRTs beschriebene Mittelungsprozess verbessert die Ergebnisse für LCDs erheblich.

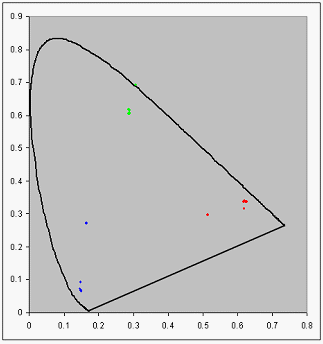
Abbildung 2 : Das Chromitätsdiagramm unter Verwendung von Daten mit angepasstem Schwarzpunkt

RGB Capture Device Model Baseline

Das grundlegende RGB-Erfassungsgerätemodell ist eine Unterklasse der IDeviceModel-Klasse. Bei der farbmetrischen Charakterisierung von Farberfassungsgeräten, z. B. Scannern und Digitalkameras, wird der folgende Ansatz verwendet. Ein Ziel, das aus Farbpatches mit bekannten CIEXYZ-Werten besteht, wird mit dem Aufnahmegerät erfasst. Das Ergebnis der Aufnahme ist ein RGB-Bitmapbild, in dem die Farbe der einzelnen Patches in einem RGB-Wert codiert ist. Diese RGB-Gerätewerte gelten spezifisch für ein bestimmtes Aufnahmegerät. Ziel der farbmetrischen Charakterisierung ist es, eine empirische Beziehung zwischen den RGB-Werten des Geräts und CIEXYZ-Werten herzustellen, oder eine mathematische Transformation von RGB zu XYZ, die das Verhalten des Aufnahmegeräts so genau wie möglich modelliert.

Eine solche mathematische Transformation kann durch Polynome niedriger Grad vernünftig modelliert werden. Dieses Verfahren ist in der Literatur ausführlich beschrieben, z. B. Kang[92], Kang[97]. In Kang[97] wird ein Ansatz berichtet, der eine Gruppe von drei Polynomen mit 3, 6, 8, 9, 11, 14 oder 20 Ausdrücken in den R-, G- und B-Variablen verwendet, während die drei Polynome jeweils in die X-, Y- und Z-Komponenten des CIEXYZ-Raums zurücktreten. Für das 20-Term-Polynom lautet die Form:

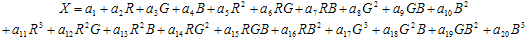
Es gibt ähnliche Ausdrücke für Y und Z. Die mathematische Technik zur Anpassung der Polynome fällt unter "Multivariate Linear Regression" und wird in jedem elementaren Text in Statistik beschrieben.

Diese Methode der linearen Regression leidet unter der Nichtminimierung der "richtigen" Objektivfunktion. Standardmäßig findet die lineare Regression die Lösung mit den geringsten Quadraten, was impliziert, dass die erhaltenen Koeffizienten die Gesamtsumme der Fehlerquadrat im zugrunde liegenden Raum oder gleichwertig die Summe der Quadrate der euklidischen Entfernungen minimieren. In der Praxis möchten Sie die Summe der Quadrate von minimieren? Es, wo ? E ist einer der akzeptierten Standards wie CIE94. Die Minimierung dieser Zielfunktion ist ein nicht lineares Regressionsproblem.

In der neuen Engine ist Lab to XYZ der CIE-Farbraum, der zurückgestellt wird, und das kubische Polynom mit 20 Begriffen wird als Modell für das Erfassungsgerät verwendet, oder Koeffizienten ls,as,bs so, dass die folgenden Polynome die Summe der Quadrate von minimieren? E _CIE94 s.

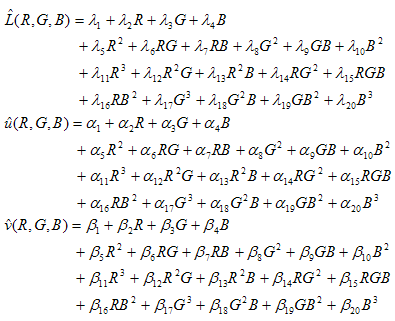
Die Lösung ( l_i, a_i, b_i ) im 60-dimensionalen realen numerischen Raum R203 muss so sein, dass der folgende Gesamtfehler minimiert wird:

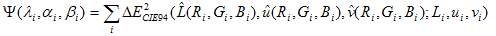
wobei die Summierung durch alle Datenpunktpaare erfolgt (R_i,Gi,Bi; L_i,ui,vi ) im Stichprobendatensatz sowie zusätzliche Kontrollpunkte, die im Folgenden beschrieben werden sollen. Dies ist ein nicht lineares Regressionsproblem, da die Parameter ? _i, a_i, * _i* treten nicht linear (nicht quadratisch) in die objektive Funktion ein.

Weil die Objective-Funktion ? ist eine nichtlineare (und nichtquadratische) Funktion der Parameter ? _i, a_i und * _i* müssen Sie auf iterative Techniken zurückgreifen, um das Optimierungsproblem zu lösen. Da die Form der Objective-Funktion eine Summe von Quadraten ist, wird eine Standardoptimierungsmethode verwendet, die als Levenberg-Marquardt-Algorithmus bezeichnet wird. Es wird als die Methode der Wahl für Probleme mit nichtlinearen kleinsten Quadraten betrachtet. Für iterative Algorithmen wie Levenberg-Marquardt müssen Sie eine erste Schätzung angeben. Eine gute anfängliche Schätzung ist in der Regel wichtig, um den richtigen Mindestwert zu finden. In diesem Fall ist ein guter Kandidat für die anfängliche Schätzung die Lösung des Problems der linearen Regression. Minimieren Sie zunächst die Summe des Quadrats der euklidischen Entfernungen im Laborraum, indem Sie eine quadratische Objektivfunktion definieren:

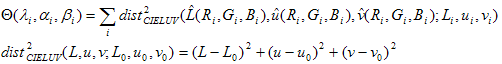
Die mathematische Lösung für solche "linearen kleinsten Quadrate" ist bekannt. Weil ? _i erscheint nur in der L-Modellierung , ein_i wird nur in der u-Modellierung und * _i* nur in der v-Modellierung angezeigt; Das Optimierungsproblem kann in drei Teilprobleme zerlegt werden: eines für L, eines für u und eines für v. Betrachten Sie die L-Formeln. (Die u-Gleichungen und die v-Formeln folgen genau demselben Argument.) Das Problem der Minimierung der Summe der Quadrate von Fehlern in L kann als Lösung der folgenden Matrixgleichung im Sinne der geringsten Quadrate angegeben werden:

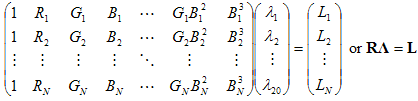
Dabei ist N die Gesamtanzahl der Datenpunkte (ursprüngliche Stichprobenpunkte plus Kontrollpunkte, die auf eine unten beschriebene Weise erstellt wurden). In der Regel ist N viel größer als 20, sodass die vorherige Gleichung überdeterminiert ist, sodass eine Lösung mit den geringsten Quadraten erforderlich ist. Eine Lösung für geschlossenes Formular für ? ist verfügbar:

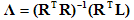
In der Praxis wird die direkte Auswertung mit der Lösung für geschlossenes Formular nicht verwendet, da sie über schlechte numerische Eigenschaften verfügt. Stattdessen wird eine Art Matrixfaktorisierungsalgorithmus auf die Koeffizientenmatrix angewendet, die das Gleichungssystem auf eine kanonische Form reduziert. In der aktuellen Implementierung wird Singular Value Decomposition (SVD) auf die Matrix R angewendet, und dann wird das resultierende zerlegte System aufgelöst.

Die Lösung für das Problem der linearen Regression, bezeichnet durch 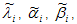, wird als Ausgangspunkt des Levenberg-Marquardt-Algorithmus verwendet. In diesem Algorithmus wird ein Testschritt berechnet, der den Punkt näher an die optimale Lösung bringen soll. Der Testschritt erfüllt eine Reihe linearer Gleichungen, die vom funktionalen Wert und den Werten der Ableitungen am aktuellen Punkt abhängig sind. Aus diesem Grund die Ableitungen der Zielfunktion ? in Bezug auf die Parameter ? _i, a_ii sind erforderliche Eingaben für den Levenberg-Marquardt Algorithmus. Obwohl es 60 Parameter gibt, gibt es eine Verknüpfung, mit der Sie viel weniger berechnen können. Durch die Verkettungsregel der Berechnung,

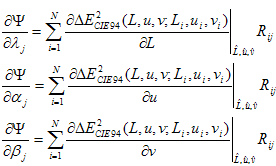
Dabei sind j = 1, 2, , 20, L_i,ui,vi der CIELAB-Wert des i. Stichprobenpunkts, und R_ij ist der (i,j )te Eintrag der oben definierten Matrix R. Anstatt also Ableitungen für 60 Parameter zu berechnen, können Sie Ableitungen fürL,a und b mithilfe der numerischen Forward-Differenz berechnen.

Es ist auch notwendig, ein Stoppkriterium für iterative Algorithmen einzurichten. In der aktuellen Implementierung werden die Iterationen beendet, wenn das mittlere quadratische DECIE94 kleiner als 1 ist oder die Anzahl der durchgeführten Iterationen 10 überschritten hat. Die Zahl 10 stammt aus der praktischen Erfahrung, dass, wenn die ersten Iterationen den Fehler nicht erheblich reduzieren, weitere Iterationen nicht viel helfen würden, als den Punkt auf oszillatorische Weise zu verschieben, d. h. der Algorithmus kann nicht konvergieren. Selbst für den Fall, dass der Algorithmus auseinandergeht, können wir sicher sein, dass die DECIE94 nicht schlechter ist als das, was wir begonnen haben, d. h. mit den Parametern, die aus der linearen Regression erhalten wurden.

Auch bei der vorangehenden Methode der nichtlinearen Regression gibt es mehrere Probleme mit der Anpassung. Ein Problem besteht darin, dass die Polynome dazu neigen, über die Datenpunkte hinaus zu über- oder unterschießen. Künstliche lokale Maxima und Minima können im Anpassungsprozess eingeführt werden. Dem kann durch die Verwendung von Polynomen mit niedrigem Grad entgegengewirkt werden, weshalb Sie nicht höher als drei Grad verwenden sollten. Ein schwerwiegenderer Aspekt des Über- oder Unterschießens ist, dass ein Polynom zwar theoretisch jeden realen Wert annehmen kann, der zu modellierende Raum jedoch in der Regel physische und praktische Einschränkungen aufweist. CIEXYZ muss alle nicht negativen Werte für X, Y, Z aufweisen, was eine physische Einschränkung ist. In der Praxis nehmen sie nur Werte in der Größenordnung von Hunderten, nicht tausende oder höher. Ebenso hat CIELAB oder CIELUV eigene physische und praktische Einschränkungen. Wenn der RGB-Raum ausreichend mit Stichprobenpunkten gefüllt ist, ist das Problem des Über- oder Unterschießens nicht schwerwiegend. Die vom Aufnahmegerät erfassten RGB-Punkte füllen den RGB-Raum jedoch in der Regel nicht gleichmäßig aus. Die Punkte können nur die inneren 80 % des RGB-Würfels füllen, oder schlimmer noch, sie können sich in einer niederdimensionalen Mannigfaltigkeit befinden. In diesem Fall können die zurückgestellten Polynome eine schlechte Arbeit beim Extrapolieren der Werte über die Datenpunkte hinaus leisten und manchmal unrealistische Vorhersagen zurückgeben. Sie möchten ein Modell, das immer einigermaßen realistische Werte zurückgibt. Dies erfordert eine Methode, die das Begrenzungsverhalten von Regressionspolynomen effektiv steuern kann, indem zusätzliche Kosten für die Polynome anfallen, die sich in der Nähe der Grenze des RGB-Cubes err statisch verhalten. Ein weiteres Measure, um sicherzustellen, dass die Polynome immer realistische Werte zurückgeben, wird angewendet, indem die Ausgabe innerhalb des CIE-Spektralorts beschnitten wird.

An diesem Punkt unterscheiden sich die Scannermodellierung und die Kameramodellierung voneinander. Es wird erwartet, dass das Kameramodell auf Regionen außerhalb der stichprobenierten Punkte extrapoliert wird, einschließlich der "Glanzlichter". Die gleiche Extrapolation ist für das Scannermodell nicht erforderlich. Es wird erwartet, dass das Scannerziel eine Charakterisierung abdeckt, die den zu scannenden gedruckten Materialien ähnelt. Das Scannermodell muss weiterhin robust sein, da es keine unrealistischen Werte zurückgeben sollte, aber eine Extrapolation weit über das Charakterisierungsziel hinaus ist nicht erforderlich. Um die Stabilität sicherzustellen, wird das oben genannte L-Polynom auf 100 beschnitten, d. h. das Polynommodell ist gezwungen, nicht über "Dmin" des Scannerziels hinaus zu extrapolieren.

Es wird erwartet, dass das Kameramodell zu Glanzlichter extrapoliert wird, sodass ein Abschneiden bei 100 nicht erwünscht ist. Stattdessen wird der folgende Algorithmus verwendet.

Künstliche Kontrollpunkte werden eingeführt, um das Verhalten der Polynome in Regionen mit unzureichender Stichprobenentnahme zu steuern. Indem sie diese Kontrollpunkte strategisch mit entsprechenden Werten platzieren, dienen sie dazu, die Polynome in die gewünschte Richtung zu "ziehen". In der aktuellen Implementierung werden acht Kontrollpunkte verwendet, die den Ecken des RGB-Cubes entsprechen. Wenn die Gerätewerte zu Unity normalisiert werden, lauten die folgenden Punkte:

R = 0, G = 0, B = 0

R = 0, G = 0, B = 1

R = 0, G = 1, B = 0

R = 0. G = 1, B = 1

R = 1, G = 0, B = 0

R = 1, G = 0, B = 1

R = 1, G = 1, B = 0

R = 1, G = 1, B = 1

Mit Ausnahme der weißen R =G =B = 1, die einem CIELAB-Wert von L = 100, u =v = 0 zugeordnet ist, wird der folgende Extrapolationsalgorithmus verwendet, um den entsprechenden CIELAB-Wert zu bestimmen, dem zugeordnet werden soll. Im Allgemeinen wird für ein bestimmtes (R,G,B ) jedem der (R_i,Gi,Bi) im stichprobenierten Dataset eine Gewichtung zugeordnet. Es gibt zwei Ziele, um die Gewichtung zuzuweisen. Erstens ist die Gewichtung umgekehrt proportional zum Abstand zwischen (R,G,B ) und (R_i,Gi,Bi). Zweitens möchten Sie Punkte verwerfen oder 0 zuweisen, die einen anderen Farbton als der angegebene Punkt (R,G,B) haben. Um den Farbton zu berücksichtigen, betrachten Sie Punkte, die in einem Kegel liegen, dessen Scheitelpunkt bei (0, 0, 0) liegt, dessen Achse mit der Linie übereinstimmt, die (0, 0, 0) zu (R, G, B ) und deren halbwinkischer Winkel ? erfüllt cos ? = 0,9. Eine Abbildung dieses Kegels finden Sie in Abbildung 3.

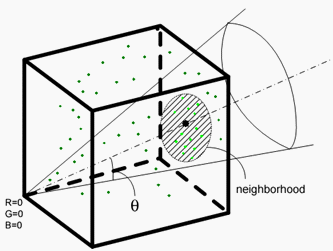
Abbildung 3 : Filtern der Stichprobenpunkte nach Winkel und Abstand. Die Form der dargestellten Nachbarschaft dient nur zu Veranschaulichungszwecken. Die tatsächliche Form hängt vom verwendeten Abstand ab. es ist eine rautenförmige Nachbarschaft, wenn die 1-Norm verwendet wird.

Innerhalb dieses Kegels wird eine zweite Filterung durchgeführt, die auf dem RGB-Abstand basiert, der die 1-Norm verwendet, definiert durch

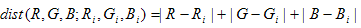
Beim aktuellen Kegel wird zunächst nach Punkten gesucht, die sich in einem Abstand von 0,1 von (R,G,B) befinden. Wenn in diesem Radius kein Punkt gefunden wird, wird der Radius um 0,1 erhöht, und die Suche wird neu gestartet. Wenn auch die nächste Runde keinen Punkt einnetzt, wird der Radius um 0,1 erhöht. Dieser Prozess wird fortgesetzt, bis der Radius MaxDist/5 überschreitet, wobei MaxDist = 3 im Fall von 1-Norm ist. Wenn kein Punkt gefunden wird, wird der Kegel vergrößert, indem die Cos verringert wird? um 0,05, d. h. Erhöhen des Winkels ? und neustarten den gesamten Prozess mit einem wachsenden Radius. Dieser Prozess wird fortgesetzt, bis eine nicht leere Gruppe von Punkten gefunden wird, oder cos ? erreicht 0, das heißt, der Kegel hat sich geöffnet, um eine Ebene zu werden. An diesem Punkt wird die Suche neu gestartet, indem der Radius vergrößert wird, mit der Ausnahme, dass die Suche fortgesetzt wird, bis der Radius MaxDist erreicht. Dadurch wird sichergestellt, dass im schlimmsten Fall eine nicht leere Gruppe von Punkten gefunden wird. Der Algorithmus ist im Flussdiagramm in Abbildung 4 zusammengefasst.

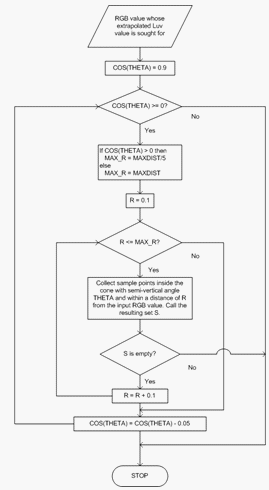
Abbildung 4 : Flussdiagramm zum Bestimmen des Satz S von Beispielpunkten, die in der Extrapolation für einen RGB-Eingabewert verwendet werden

Unter der Annahme, dass der vorangehende Prozess einen nicht leeren Satz S von Punkten (R_i,Gi,Bi ) und entsprechenden (L_i,ai,bi) ergibt, wird für jeden solchen Punkt eine Gewichtung w_i zugewiesen, gegeben durch

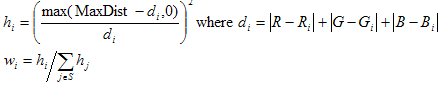
Schließlich wird der Extrapolant definiert durch

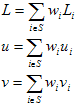
Die obigen Formeln bilden eine instance der "inverse-distance weighted methods", die häufig als Shepard-Methoden bezeichnet werden. Durch Ausführen jeder der acht Punkte von eq (6) durch den Algorithmus werden acht Kontrollpunkte mit jeweils R-, G-, B- und L,a,b-Werten abgerufen, die mit den ursprünglichen Beispieldaten in den Pool eingefügt werden.

Um sicherzustellen, dass das Modell immer gültige Farbwerte erzeugt, und für Systemintegrität und Stabilität in der gesamten Farbverarbeitungspipeline müssen Sie einen endgültigen Clipping an der Ausgabe des Polynommodells durchführen. Der visuelle CIE-Gamut wird durch die achromatische Komponente (Y oder L ) und die chromatische Komponente (xy oder a'b' beschrieben, die durch eine projektive Transformation mit dem XYZ-Raum verbunden sind). In der aktuellen Implementierung wird die a'b' -Chromatik verwendet, da sie direkt mit dem CIELUV-Raum verknüpft ist. Für einen beliebigen CIELAB-Wert klammern Sie zuerst L in einen nicht negativen Wert:

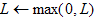
Um eine Extrapolation für Glanzlichter zu ermöglichen, wird L nicht bei 100 beschnitten, der "herkömmlichen" Obergrenze für L im Laborraum.

Wenn L = 0 ist, werden a und b so beschnitten, dass a*= b =* 0. Wenn L ? 0, berechnen

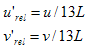
Dies sind die Komponenten eines Vektors im a'b' -Diagramm vom Weißpunkt (u?',v?' ) bis zur betreffenden Farbe. Definieren Sie den spektralen CIE-Locus als konvexen Rumpf aller Punkte (a',b' ), parametrisiert durch die Wellenlänge ?:

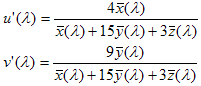
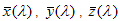sind die CIE-Farbabgleichsfunktionen für den 2-Grad-Beobachter. Wenn der Vektor außerhalb des CIE-Locus liegt, wird die Farbe auf den Punkt des CIE-Locus abgeschnitten, der der Schnittpunkt des Locus und der durch den Vektor definierten Linie ist. Weitere Informationen in Abbildung 5. Wenn ein Clipping erfolgt ist, wird der a - und b-Wert rekonstruiert, indem zuerst a?' und b? von den beschnittenen a' und b' subtrahiert und dann mit 13 L multipliziert werden.

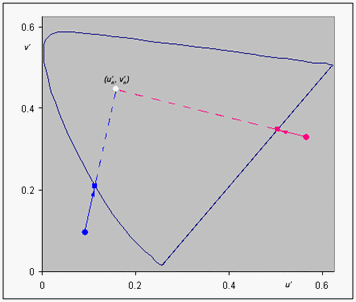
Abbildung 5 : Beschneidungsalgorithmus für Lab-Werte, die sich außerhalb des visuellen CIE-Gamuts befinden

In der aktuellen Implementierung wird der CIE-Spektral locus in der a'b'- Ebene durch eine stückweise lineare Kurve mit 35 Segmenten dargestellt (entspricht einer Wellenlänge von 360 nm bis einschließlich 700 nm). Indem die Liniensegmente so angeordnet werden, dass ihre untergeordneten Winkel am Weißen Punkt aufsteigend sind, was absteigenden Wellenlängen entspricht, kann das Liniensegment, das sich mit dem Strahl überschneidet, der durch den obigen Vektor gebildet wird, durch eine einfache binäre Suche gefunden werden.

RGB-Druckergerätemodell – Baseline

Eine Gerätecharakterisierung eines RGB-Druckers besteht aus der Erstellung eines empirischen Modells des Geräts, das die geräteunabhängige CIELUV-Farbe für einen bestimmten RGB-Wert vorhersagt.

Es gibt zwei Möglichkeiten, das empirische Modell zu konstruieren. Eine Möglichkeit besteht darin, die Gerätedaten für einen RGB-Drucker zu verwenden, die andere ist die Verwendung analytischer Parameterdaten. In der ersten werden von einem Benutzer für ein RGB-Druckergerät bereitgestellte Messdaten verwendet, um eine 3D-Nachschlagetabelle (LUT) zu erstellen. Die Messdaten bestehen aus XYZ-Werten für einheitliche RGB-Patches. Typische Stichprobengrößen sind 9 oder 17 für jede Komponente. Jeder Patch wird mit einem Farbmesser oder Spektrophotometer im CIEXYZ-Raum gemessen. Der XYZ-Wert für einen Patch wird dann in den CIELUV-Wert konvertiert, der eine 3D-LUT bildet. Im Gerätemodell wird die tetraedrale Interpolationsmethode von Sakamoto auf die 3D-LUT angewendet, um die CIELUV-Daten für eine bestimmte RGB-Daten vorherzusagen. (Confer US Patent 4275413 (Sakamoto et al.), US Patent 4511989 (Sakamoto), Kang [1]. Die beiden genannten Patente sind abgelaufen.). Die analytischen Parameterdaten, die in der zweiten Methode übergeben werden, sind einfach eine zuvor erstellte LUT. In der Regel wurde diese LUT mit der ersten Methode erstellt, obwohl sie von Hand erstellt werden konnte.

In der aktuellen Farbverwaltung ist die Quellzuordnung als die Karte definiert, die vom RGB-Raum zu einem geräteunabhängigen CIEXYZ-Farbraum wechselt. Die Zielzuordnung ist definiert als die Karte, die vom geräteunabhängigen CIEXYZ-Farbraum zum RGB-Bereich wechselt. Dies ist die Umkehrung der Quellzuordnung.

Das empirische Modell wird direkt in der Quellzuordnung verwendet. Es ordnet zunächst eine bestimmte RGB-Daten in CIELUV-Daten zu, die in XYZ-Daten konvertiert werden. In der Zielzuordnung werden zunächst geräteunabhängige CIEXYZ-Daten in CIELUV-Daten konvertiert. Anschließend werden das empirische Modell und die klassische Newton-Raphson-Methode verwendet, um die besten RGB-Daten für die CIELUV-Daten vorherzusagen. Die Details zur Konvertierung von CieLUV in RGB-Daten lauten wie folgt:

Nach dem Generieren einer 3D-LUT von RGB zu CieLUV wird die Karte von RGB zu LUV mithilfe der tetraedralen Interpolation auf RGB erstellt. Diese Zuordnung wird durch die folgenden Formeln gekennzeichnet:

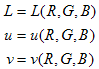
Inversion der Karte besteht aus dem Lösen, für jede Farbe 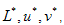, das folgende System von nichtlinearen Formeln:

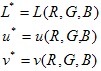
Im neuen CTE wird eine nicht lineare Gleichung verwendet, die auf der klassischen Newton-Raphson-Methode basiert. Eine anfängliche Schätzung oder a priori siehe, s _prior -(R 0, G 0, B 0 ) wird durch Durchsuchen einer "Startmatrix" erhalten, die aus einem einheitlichen 8x8x8-Raster von vorgerechneten (RGB, Luv)-Paaren besteht. Es wird die RGB-entsprechende Luv ausgewählt, die der L*u*v* am nächsten liegt. Jeder Punkt in der Ausgangsmatrix entspricht der Mitte einer Zelle, sodass die Iterationen nicht mit einem Punkt auf der Begrenzungsseite des RGB-Cubes beginnen. Mit anderen Worten, die RGB der Samen wird definiert durch: STEP = 1/8 s _ijk = (STEP/2 + (i-1) STEP, STEP/2+(j-1)STEP, STEP/2+(k-1)STEP) mit i,j,k = 1...8 Im ersten Schritt von Newton-Raphson zeigt die nächste Schätzung 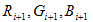mit der Formel:

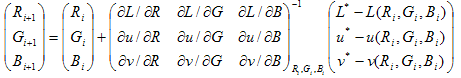
Die Iteration wird beendet, wenn der Fehler (Abstand im CIELUV-Bereich) kleiner als eine vordefinierte Toleranzstufe (0,1 im CTE) ist oder wenn die Anzahl der Iterationen die maximal zulässige Anzahl von Iterationen überschritten hat (10 im CTE). Die Werte für die Toleranz und die Anzahl der Iterationen wurden empirisch als effektiv bestimmt. In zukünftigen Versionen kann der Toleranzwert geändert werden.

Die Jacobsche Matrix wird mithilfe der Vorwärtsdifferenz berechnet, außer an einem Begrenzungspunkt (mindestens ein r, G, B ist 1), wo stattdessen die Rückwärtsdifferenz verwendet wird. Anstatt die Umkehrung der Jakobsmatrix zu berechnen, wird das lineare System direkt gelöst, indem Gauss-Jordan Eliminierung mit vollständiger Pivotierung verwendet wird.

Am Ende der Iterationen wird möglicherweise noch keine Konvergenz erreicht, da Newton-Raphson ein "lokaler" Algorithmus ist, d. h. es funktioniert nur gut, wenn Sie mit einer anfänglichen Schätzung beginnen, die nahe an der tatsächlichen Lösung liegt. Wenn am Ende der Newton-Raphson Iterationen keine Konvergenz innerhalb der vordefinierten Fehlertoleranz erreicht wurde, werden die Iterationen mit einem neuen Satz von Samen neu gestartet, der wie folgt definiert ist.

Die bisher beste Lösung ist beispielsweise (r, g, b). Aus dieser Lösung werden N a posteriori-Samen abgeleitet, wobei N = 4. Intuitiv wird die Lösung "in Richtung Mitte" in einer Schrittgröße verschoben, die von N abhängt. Siehe Abbildung 6.

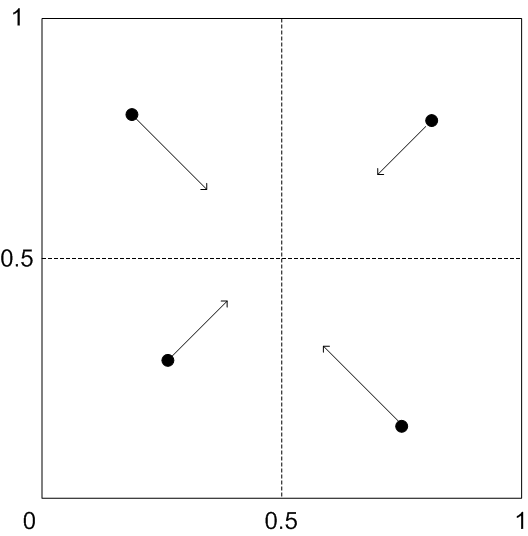
Abbildung 6 : Die Störrichtung der Lösung hängt davon ab, in welchem Oktant sie sich befindet.

Mit anderen Worten, wenn r > 0,5, wird der Wert auf dem R-Kanal verringert, andernfalls wird der Wert erhöht. Es gibt eine ähnliche Logik für die G- und B-Kanäle. Die genauen Definitionen sind:

PERTURBATION = 0,5/(N+1)

Dir(r) = -1, wenn r > 0,5; andernfalls +1. Ähnlich für Dir(g) und Dir(b)

Der jth a posteriori Seed, s ????, ist (r + Dir(r) *j * PERTURBATION, g + Dir(g) * j * PERTURBATION, b + Dir(b) * j * PERTURBATION)

Probieren Sie die erste s-???? und wenn es eine neue Lösung innerhalb der Fehlertoleranz bietet, können Sie beenden. Andernfalls versuchen Sie den zweiten s ???? usw. bis zum Nth s ????.

Die Schemas des gesamten Algorithmus sind in Abbildung 7 dargestellt.

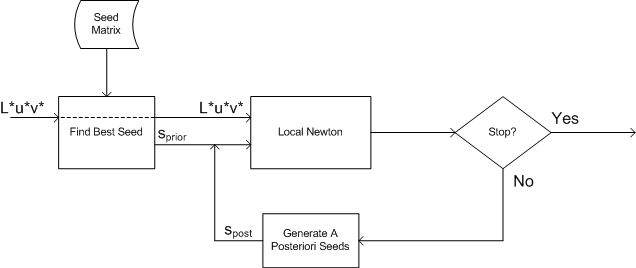
Abbildung 7 : Schematische Darstellung der Invertierung des Gerätemodells

Baseline des RGB-Modells für virtuelle Geräte

Dieses Gerätemodell (DM) ist ein einfacher Algorithmus für die Matrix-/Tonwiedergabe. Die Matrix wird vom Weißpunkt und den Vorwahlen mithilfe von Standardfarbwissenschaftsalgorithmen abgeleitet. Die Tonwiedergabekurve wird von den Messparametern gemäß den ICC-Beschreibungen von CurveType und ParametricType abgeleitet (oder nach Bedarf invertiert). Details zu den internen Algorithmen werden nach einer zusätzlichen Validierung von Problemen mit hohem Dynamischen Bereich bereitgestellt.

Das virtuelle RGB-Gerätemodell ist eine idealisierte Matrix-Ton-Reproduktionskurve RGB, die dem drei komponentenbasierten ICC-matrixbasierten Profilentwurf ähnelt. Die Parameter "virtuelle Messung" des DM umfassen einen Weißpunktwert (absolutes CIEXYZ), RGB-Primärwerte (absolutes CIEXYZ) und eine Tonwiedergabekurve, die auf dem ICC ParametricCurveType und CurveType in der XML-Formatierung basiert, die mit den DMP-Schemas konsistent ist.

Die ICC parametricCurveType-Funktionstypcodierung und die entsprechende Unterstützung in IRGBVirtualDeviceModelBase sind in der folgenden Tabelle dargestellt.

Funktionstyp	Parameter	type	Hinweis
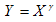
	g	GammaType	Allgemeine Implementierung
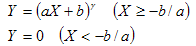
	ga b	GammaOffsetGainType	CIE 122-1966
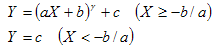
	ga b c	GammaOffsetGainOffsetType	IEC 61966-3
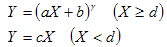
	ga b c d	GammaOffsetGainGainType	IEC 61966-2.1 (sRGB)
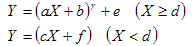
	ga b c d e f	–	In WCS nicht unterstützt

Die Tonkurve für virtuelle RGB-Geräte wird in DeviceToColorimetric zwischen den Eingabedaten, pDeviceColors und der Matrix multiplizieren angewendet. Für ColorimetricToDevice muss eine Methode verwendet werden, um die Tonkurve umzukehren. In der Baselineimplementierung erfolgt dies durch direkte Interpolation in derselben Tonkurve, die für DeviceToColorimetric verwendet wird.

Die Kurven sollten in den Profilen als Zahlenpaare im Gleitkommaraum angegeben werden. Die erste Zahl stellt Werte in pDeviceColors dar. Die zweite Zahl stellt die Ausgabe der Tonkurve dar. Alle Werte in der Tonkurve müssen zwischen minColorantUsed und maxColorantUsed sein. Tonkurven müssen mindestens zwei Einträge enthalten: einen für minColorantUsed und einen für maxColorantUsed. Die maximale Anzahl von Einträgen im ToneCurve ist 2048. Im Allgemeinen können Sie die Krümmung genauer modellieren, je mehr Einträge in der Tabelle vorhanden sind. Zwischen den Einträgen wird eine stückweise lineare Interpolation durchgeführt.

Sie können alternative Interpolationsmethoden in Betracht ziehen. Wenn Sie etwas über das zugrunde liegende Verhalten des Geräts wissen, können Sie weniger Beispiele verwenden und mit einer Kurve höherer Reihenfolge genauer modellieren. Wenn Sie jedoch den falschen Kurventyp verwenden, sind Sie sehr ungenau. Ohne weitere Informationen können Sie den Kurventyp nicht erraten. Verwenden Sie daher die lineare Interpolation, und stellen Sie viele Datenpunkte bereit.

CMYK-Druckergerätemodellbaseline

Eine Gerätecharakterisierung eines CMYK-Druckers besteht aus der Erstellung eines empirischen Modells des Geräts, das die gedruckte Farbe für einen bestimmten CMYK-Wert vorhersagt. Die Charakterisierung umfasst auch die Inversion dieses Modells, sodass eine Verschreibung des CMYK-Werts an uns für eine bestimmte zu druckende Farbe gegeben werden kann. Dies wird in der Regel als CIEXYZ- oder CIELAB-Wert definiert.

In der Regel wird ein IT8.7/3-Ziel mit CMYK-Patches verwendet. Die Patches bestehen aus der Stichprobenentnahme des CMYK-Raums in einer klar definierten Weise, sodass ein rechteckiges Raster (mit nicht gleichmäßigem Abstand in C, M, Y und K) gebildet wird. Jeder Patch wird dann mit einem Colorimeter oder Spectrophotometer gemessen. Die Messungen in CIEXYZ-Werten bilden dann eine Nachschlagetabelle (LUT), aus der ein empirisches Modell des Druckers mithilfe der Interpolationsmethode von Sakamoto erstellt wird. US Patent 4275413 (Sakamoto et al.), US Patent 4511989 (Sakamoto), Kang [1]. Die beiden genannten Patente sind abgelaufen.

Die spezifischen Anforderungen an die CMYK-Messproben, die erforderlich sind, damit ein Gerätemodellprofil vom CMYK-Druckerbaselinegerätemodell als gültig akzeptiert wird, sind die folgenden: (Der Beispielsatz wird am deutlichsten als eine Gruppe von CMY-Beispielwürfeln beschrieben, die jeweils einer bestimmten K-Ebene zugeordnet sind.)

• Mindestens müssen gültige CMY-Cubes für die Ebenen K = 0 und K = 100 bereitgestellt werden.

• Mittlere K-Ebenen können ungleich gleichmäßig angeordnet sein.

• Jede mittlere K-Ebene ohne gültigen CMY-Cube wird ignoriert.

• Die CMY-Cubes können nicht einheitliche Stichprobenintervalle (Rasterabstand) verwenden, aber derselbe Satz von Beispielintervallen muss in allen C,M- und Y-Dimensionen im CMY-Cube für eine bestimmte K-Ebene verwendet werden.

• Jeder CMY-Cube auf K-Ebene kann eine andere Anzahl und einen anderen Abstand von Beispielintervallen verwenden.

• Alle CMY-Cubes müssen die "Ecken" des CMY-Cubes enthalten, d. CMY-Beispiele bei [0,0,0], [0,0,100], [0,100,0], [100,0,0], [0,100,100], [100,0,100], [100,100, [100,100, 0], [100,100,100].

• Alle mittleren CMY-Rasterebenen müssen in jedem Kanal vollständig stichprobeniert werden. Mit anderen Worten, ein Beispiel muss an jeder 3D-Rasterschnittstelle innerhalb des CMY-Cubes vorhanden sein.

• Für die Cubes K = 0 und K = 100 CMY sind 2x2 "nur Ecken" die Mindestwürfel, die als gültig akzeptiert werden.

  [HINWEIS: Für K=0- und K=100-Ebenen wird ein 3x3x3 CMY-Cube als 2x2x2-Cube "nur Ecken" verarbeitet; die mittlere Beispielebene wird ignoriert. In größeren Cubes von 4x4x4 werden alle Rasterbeispiele verwendet.]

• Für mittlere K-Ebenen sind 4x4x4 CMY-Cubes das Minimum, das als gültig akzeptiert wird.

Ein hochwertiges Profil verwendet feinere Stichprobengitter als das für die Gültigkeit erforderliche Minimum, in der Regel 9x9x9x9 oder höher. Die Beispiele aus den Zielen IT8.7/3, IT8.7/4 und ECI erzeugen gültige Gerätemodellprofile (DMPs) für das CMYK-Druckerbaselinegerätemodell. Obwohl dieses Gerätemodell in der Lage ist, die fremdförmigen (off-grid)-Stichproben in diesen Zielen zu ignorieren, ist es nicht garantiert, dass dies für andere Ziele möglich ist. Daher wird empfohlen, fremdförmige Proben aus Messsätzen zu entfernen, die in Profile für dieses Gerätemodell eingehen.

Die Inversion des Druckermodells stellt mehr Schwierigkeiten dar. Bei einer Eingabefarbe in CIECAM stellt sich die Frage, ob diese Farbe innerhalb des Druckerumfangs liegt. Es gibt auch das Problem in Bezug auf die Anordnung von Punkten im Farbdarstellungsraum. Während wir die CMYK-Werte so anordnen können, dass sie auf einem rechteckigen Raster fallen, wie dies im IT8.7/3-Ziel der Fall ist, kann dasselbe nicht für die resultierenden gedruckten Farben gesagt werden, da sie sich im Farbdarstellungsraum befinden. Im Allgemeinen sind sie im Farbdarstellungsraum ohne bestimmtes Muster verstreut.

Es gibt im Allgemeinen zwei Ansätze für das Inversionsproblem von punktierten Punkten. Ein Ansatz besteht darin, eine geometrische Unterteilung der Druckerskala mit elementaren 3-dimensionalen Festkörpern wie Tetraeder zu verwenden. Eine Unterteilung der Druckerskala im Farbdarstellungsbereich kann aus der entsprechenden Unterteilung des CMY(K)-Raums induziert werden, siehe Hung[93], Kang[97]. Dieser Ansatz hat den Vorteil der rechentechnischen Einfachheit. Bei einem Tetraeder werden nur vier Punkte in einer Interpolation verwendet. Andererseits hängt das Ergebnis stark von wenigen Punkten ab, was bedeutet, dass ein Messfehler erhebliche Auswirkungen auf das Ergebnis hat. Der Interpolant ist auch tendenziell nicht so glatt. Der zweite Ansatz setzt keine Unterteilung voraus und basiert auf der Technik der Streudateninterpolation. Ein klassisches Beispiel ist die Technik der Shepard-Interpolation oder umgekehrt gewichtete Methode (siehe Shepard [68]). Hier werden mehrere Punkte, die den Eingabepunkt umgeben, in irgendeiner Weise ausgewählt, wobei jedem eine Gewichtung zugewiesen wird, die in der Regel umgekehrt proportional zur Entfernung ist, und der Interpolant wird als gewichteter Mittelwert der benachbarten Punkte verwendet. Bei diesem Ansatz ist die Auswahl der benachbarten Punkte von größter Bedeutung für die Leistung. Während zu wenige Punkte die Interpolanten ungenau und unglättend rendern können, verursachen zu viele Punkte hohe Berechnungskosten, da die Gewichtungen in der Regel nicht lineare Funktionen und kostenintensiv in der Berechnung sind.

Die beiden oben beschriebenen Ansätze haben Probleme. Der Unterteilungsansatz hängt entscheidend davon ab, dass die Daten einigermaßen rauschfrei sind, und im Allgemeinen ist der Interpolant nicht sehr glatt. Die Interpolation von gestreuten Daten ist toleranter gegenüber Datenrauschen und bietet im Allgemeinen einen reibungsloseren Interpolanten, ist aber rechnerisch teurer.

Der neue CTE verfolgt einen alternativen Ansatz. Das CMYK-Gerät wird als Sammlung mehrerer CMY-Geräte behandelt, von denen jedes den spezifischen Wert Schwarz (K) aufweist. Mit einem Auswahlalgorithmus, der als Parameter Die Helligkeit und Chroma annimmt, wird ein Grad von Schwarz ausgewählt. Die CMY-Werte werden durch Inversion der entsprechenden CMY zu Luv-Tabelle mithilfe der Newton-Methoden abgerufen, die an anderer Stelle vom RGB-Druckeralgorithmus verwendet werden.

Führen Sie die folgenden Schritte aus:

1. Drucken Sie das Charakterisierungsziel, bei dem es sich entweder um das IT8.7/3-Ziel oder ein Ziel handelt, das das Sampling des CMYK-Raums in regelmäßigen oder unregelmäßigen Abständen enthält.
2. Messen Sie das Ziel mithilfe eines Spektrophotometers, und konvertieren Sie die Messungen in den CIELUV-Raum.
3. Erstellen Sie die Vorwärtskarte von CMYK zu Luv.
4. Verwenden Sie die Vorwärtszuordnung, um eine Gruppe von CMY- zu Luv-Karten für einen Bereich von K-Werten zu erstellen.
5. Für jeden Luv-Eingabewert wird der entsprechende CMYK-Wert abgerufen, indem eine der in Schritt 4 oben erstellten Karten ausgewählt und mithilfe der Newton-Methode invertiert wird, um einen CMY-Farbstoffsatz zu erhalten, der den ausgewählten K-Wert begleitet.

Die Schritte 1 und 2, bei denen es sich um Standardverfahren handelt, werden von einem Profilerstellungsprogramm ausgeführt, das nicht Teil des neuen CTE ist. Das IT8.7/3-Ziel enthält eine einigermaßen detaillierte Stichprobenentnahme aller CMYK-Werte auf verschiedenen Ebenen von C, M, Y und K. Alternativ kann ein benutzerdefiniertes Ziel mit einheitlicher Stichprobenentnahme der Kanäle C, M, Y und K verwendet werden. Nachdem das Ziel gedruckt wurde, kann ein Spektrophotometer oder Farbmeter verwendet werden, um den XYZ-Wert jedes Patches zu messen, und der XYZ-Wert kann mithilfe des CIELUV-Modells in den Luv-Wert konvertiert werden.

Schritt 3, die Konstruktion der Vorwärtskarte von CMYK zu Luv, kann erreicht werden, indem jede bekannte Interpolationstechnik, wie tetraedrale oder mehrlineare Methode, auf das rechteckige Raster im CMYK-Raum angewendet wird. Im neuen CTE wird eine vierdimensionale tetraedrale Interpolation verwendet. Da die CMY-Samplingraster in der Regel auf jeder Ebene von K unterschiedlich sind, verwenden wir jedoch eine Super-Sampling-Methode, wie unten beschrieben. Für einen bestimmten CMYK-Punkt werden zunächst die Sandwiching-K-Ebenen basierend auf dem K-Wert bestimmt. Führen Sie dann ein "Superraster" auf jeder K-Ebene ein, das eine Vereinigung der CMY-Raster auf jeder der beiden K-Ebenen ist. Auf jeder K-Ebene wird der Luv-Wert eines neu eingeführten Gitterpunkts durch eine dreidimensionale tetraedrale Interpolation innerhalb dieser K-Ebene abgerufen. Schließlich wird in diesem neuen Raster eine vierdimensionale tetraedrale Interpolation für den spezifischen CMYK-Punkt durchgeführt.

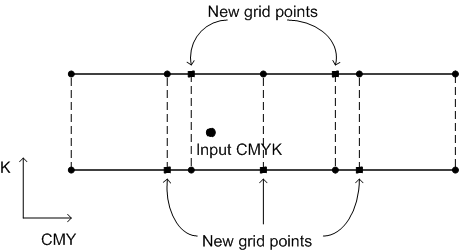
Abbildung 8 : Supersampling

Schritt 4 erstellt eine Reihe von CMY-zu-Luv-Nachschlagetabellen (LUTs). Die in Schritt 3 erstellte Vorwärtszuordnung wird wiederholt aufgerufen, um den CMYK-Raum neu zu erfassen. Der CMYK-Farbraum wird mit einem gleichmäßigen Abstand von K und einer anderen, aber immer noch gleichmäßigen Stichprobenentnahme von CMY abgetastet.

Schritt 5 ist ein Verfahren zum Abrufen des CMYK-Werts mithilfe der in Schritt 4 erstellten LUTs für einen beliebigen Luv-Eingabepunkt. Der geeignete Wert von K wird ausgewählt, indem die Helligkeit sowie der Grad der Farbe in der angeforderten Luv analysiert werden. Nachdem die Tabelle ausgewählt wurde, werden die CMY-Werte mithilfe der Newton-Methode aus der Tabelle abgerufen (wie unter dem RGB-Druckergerätemodell zuvor dokumentiert).

Der CIELUV-Speicherplatz wird im Druckermodell anstelle von CIEJab verwendet, da das Gerätemodell ausschließlich auf farbmetrischen Daten basieren sollte, die im DMP verfügbar sind. Der DMP enthält farbmetrische Daten für jeden gemessenen Patch, einschließlich des Medienweißpunkts, sodass es möglich ist, CIEXYZ-Daten in CIELUV-Daten zu konvertieren. Es ist jedoch nicht möglich, in CIECAM02 JCh oder Jab zu konvertieren, da es keinen Zugriff auf die Anzeigebedingungsinformationen im DMP gibt.

Baseline des RGB-Projektorgerätemodells

Hinweis: Viele RGB-Projektoren verfügen über mehrere Betriebsmodi. In einem Modus, der häufig der Standard ist und als "Präsentation" bezeichnet werden kann, wird die Farbantwort des Projektors für maximale Helligkeit optimiert. In diesem Modus verliert der Projektor jedoch die Fähigkeit, Licht, leicht chromatische Farben wie blassgelb und einige Fleischtöne zu reproduzieren. In einem anderen Modus, der oft als "Film", "Video" oder "sRGB" bezeichnet wird, ist der Projektor für die Wiedergabe realistischer Bilder und Naturszenen optimiert. In diesem Modus wird die maximale Helligkeit getauscht, um die Gesamtqualität der Farbwiedergabe zu verbessern. Um eine zufriedenstellende Farbwiedergabe mit RGB-Projektoren zu erhalten, ist es notwendig, den Projektor in einen Modus zu platzieren, in dem eine glatte Farbskala reproduziert werden kann.

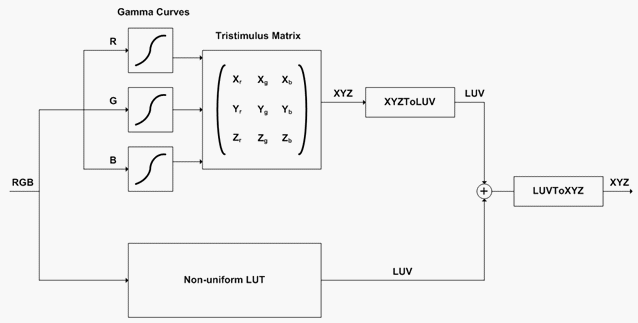
Abbildung 9 : DLP-Gerätemodell

Ein eingehender RGB-Wert durchläuft zwei Berechnungspfade. Das erste ist das Matrixmodell, das zu einem XYZ-Wert führt. Unmittelbar darauf folgt die Konvertierung von XYZ zu Luv. Die zweite ist die nicht einheitliche LUT-Interpolation mit tetraedraler Interpolation. Die Ausgabe der Interpolation befindet sich bereits im Luv-Raum. Die beiden Ausgaben werden hinzugefügt, um den vorhergesagten Luv-Wert zu erhalten. Dies wird schließlich in XYZ konvertiert. Dies ist die erwartete Ausgabe des farbmetrischen Modells für das DLP-Gerät.

Da Projektoren Anzeigegeräte sind, unterstützen sie auch die Inversion des Modells, d. h. die Transformation von XYZ zu RGB. Da das Gerätemodell RGB-Raum in XYZ-Raum transformiert, die beide dreidimensional sind, entspricht die Inversion dem Lösen von drei nichtlinearen Formeln in drei unbekannten Elementen. Dies kann durch Standardgleichungslösungstechniken wie Newton-Raphson erfolgen. Es ist jedoch vorzuziehen, zuerst XYZ in Luv zu konvertieren und dann die Luv-In-RGB-Transformation umzukehren, da der Luv-Raum wahrlich linearer ist als XYZ-Raum.

ICC-Gerätemodellbaseline

Die CITE ICC-Workflowinteroperabilität wird aktiviert, indem ein spezielles ICC-Gerätebaseline-Gerätemodellprofil erstellt wird, das das Profilobjekt speichert und eine ICC-Transformation mithilfe eines XYZ-Profils ohne Op-Funktion erstellt. Diese Transformation wird dann verwendet, um zwischen Geräte- und CIEXYZ-Farben zu übersetzen.

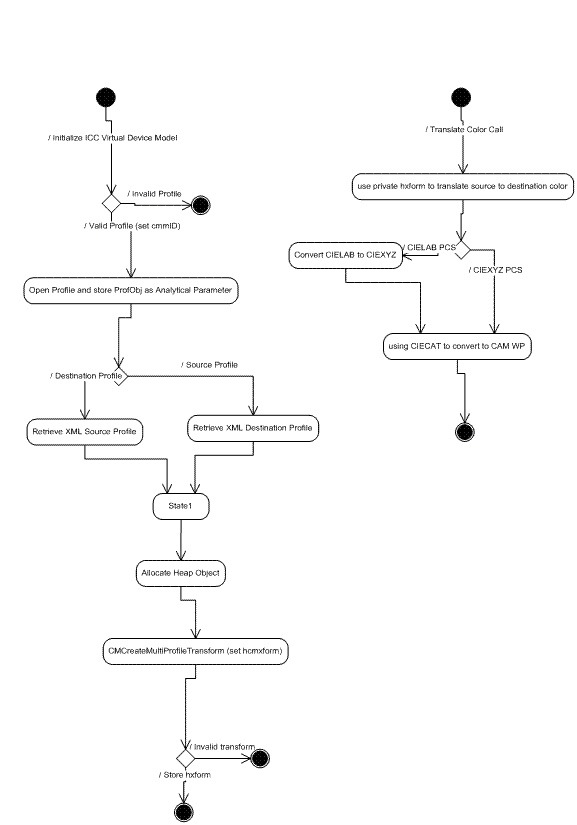
Abbildung 10 : CITE ICC-Workflowinteroperabilität

Zugehörige Themen

Grundlegende Farbverwaltungskonzepte

Windows Color System: Schemas und Algorithmen