Globale und lokale Transformationen

Eine globale Transformation ist eine Transformation, die für jedes Element gilt, das von einem bestimmten Graphics-Objekt gezeichnet wird. Um eine globale Transformation zu erstellen, erstellen Sie ein Graphics-Objekt, und rufen Sie dann die Graphics::SetTransform--Methode auf. Die Graphics::SetTransform-Methode bearbeitet ein Matrix--Objekt, das dem Graphics-Objekt zugeordnet ist. Die in diesem Matrix Objekt gespeicherte Transformation wird als Welttransformationbezeichnet. Die Welttransformation kann eine einfache affine Transformation oder eine komplexe Sequenz von affinen Transformationen sein, aber unabhängig von ihrer Komplexität wird die Welttransformation in einem einzigen Matrix--Objekt gespeichert.

Die klasse Graphics bietet mehrere Methoden zum Aufbau einer zusammengesetzten Welttransformation: Graphics::Multipliziertransform, Graphics::RotateTransform, Graphics::ScaleTransformund Graphics::TranslateTransform. Im folgenden Beispiel wird zweimal eine Auslassungspunkte ellipse bezieht: einmal vor dem Erstellen einer Welttransformation und einmal danach. Die Transformation skaliert zuerst um den Faktor 0,5 in y-Richtung, übersetzt dann 50 Einheiten in x-Richtung und dreht dann 30 Grad.

myGraphics.DrawEllipse(&myPen, 0, 0, 100, 50);
myGraphics.ScaleTransform(1.0f, 0.5f);
myGraphics.TranslateTransform(50.0f, 0.0f, MatrixOrderAppend);
myGraphics.RotateTransform(30.0f, MatrixOrderAppend);
myGraphics.DrawEllipse(&myPen, 0, 0, 100, 50);

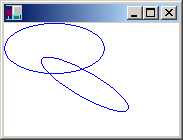
Die folgende Abbildung zeigt die ursprüngliche Ellipse und die transformierte Ellipse.

Anmerkung

Im vorherigen Beispiel wird die Ellipse um den Ursprung des Koordinatensystems gedreht, das sich in der oberen linken Ecke des Clientbereichs befindet. Dies führt zu einem anderen Ergebnis als das Drehen der Auslassungspunkte über die eigene Mitte.

 

Eine lokale Transformation ist eine Transformation, die für ein bestimmtes Element gilt, das gezeichnet werden soll. Ein GraphicsPath--Objekt verfügt beispielsweise über eine GraphicsPath::Transform-Methode, mit der Sie die Datenpunkte dieses Pfads transformieren können. Das folgende Beispiel zeichnet ein Rechteck ohne Transformation und einen Pfad mit einer Drehungstransformation. (Gehen Sie davon aus, dass es keine Welttransformation gibt.)

 
Matrix myMatrix;
myMatrix.Rotate(45.0f);
myGraphicsPath.Transform(&myMatrix);
myGraphics.DrawRectangle(&myPen, 10, 10, 100, 50);
myGraphics.DrawPath(&myPen, &myGraphicsPath);

Sie können die Welttransformation mit lokalen Transformationen kombinieren, um eine Vielzahl von Ergebnissen zu erzielen. Beispielsweise können Sie die Welttransformation verwenden, um das Koordinatensystem zu überarbeiten und lokale Transformationen zu verwenden, um Objekte zu drehen und zu skalieren, die im neuen Koordinatensystem gezeichnet wurden.

Angenommen, Sie möchten ein Koordinatensystem mit dem Ursprung 200 Pixel vom linken Rand des Clientbereichs und 150 Pixel vom oberen Rand des Clientbereichs. Gehen Sie außerdem davon aus, dass die Maßeinheit das Pixel sein soll, wobei die x-Achse nach rechts und die Y-Achse nach oben zeigt. Das Standardkoordinatensystem weist die Y-Achse nach unten auf, sodass Sie eine Spiegelung über die horizontale Achse ausführen müssen. Die folgende Abbildung zeigt die Matrix einer solchen Spiegelung.

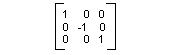
Gehen Sie als Nächstes davon aus, dass Sie eine Übersetzung von 200 Einheiten nach rechts und 150 Einheiten nach unten durchführen müssen.

Im folgenden Beispiel wird das soeben beschriebene Koordinatensystem festgelegt, indem die Welttransformation eines Graphics-Objekts festgelegt wird.

Matrix myMatrix(1.0f, 0.0f, 0.0f, -1.0f, 0.0f, 0.0f);
myGraphics.SetTransform(&myMatrix);
myGraphics.TranslateTransform(200.0f, 150.0f, MatrixOrderAppend);

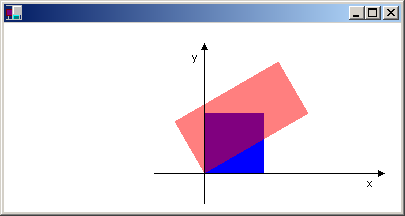
Der folgende Code (platziert nach dem Code im vorherigen Beispiel) erstellt einen Pfad, der aus einem einzelnen Rechteck mit seiner unteren linken Ecke am Ursprung des neuen Koordinatensystems besteht. Das Rechteck wird einmal ohne lokale Transformation und einmal mit einer lokalen Transformation gefüllt. Die lokale Transformation besteht aus einer horizontalen Skalierung um einen Faktor von 2, gefolgt von einer 30-Grad-Drehung.

// Create the path.
GraphicsPath myGraphicsPath;
Rect myRect(0, 0, 60, 60);
myGraphicsPath.AddRectangle(myRect);

// Fill the path on the new coordinate system.
// No local transformation
myGraphics.FillPath(&mySolidBrush1, &myGraphicsPath);

// Transform the path.
Matrix myPathMatrix;
myPathMatrix.Scale(2, 1);
myPathMatrix.Rotate(30, MatrixOrderAppend);
myGraphicsPath.Transform(&myPathMatrix);

// Fill the transformed path on the new coordinate system.
myGraphics.FillPath(&mySolidBrush2, &myGraphicsPath);

Die folgende Abbildung zeigt das neue Koordinatensystem und die beiden Rechtecke.