Freigeben über

Parameterkurven

  • Artikel

Medienparameter können im Laufe der Zeit einer Kurve folgen. Jede Kurve wird durch eine mathematische Formel und zwei Endpunkte beschrieben. Jeder Endpunkt wird durch eine Referenzzeit und den Wert der Kurve zu diesem Zeitpunkt definiert. Die Formel wird verwendet, um Zwischenwerte zwischen den Punkten zu berechnen, und bestimmt die Form der Kurve. Die möglichen Kurven sind:

  • Springen
  • Linear
  • Square
  • Umgekehrtes Quadrat
  • Sinus

"Jump" bedeutet, direkt zum Endwert zu springen. Die anderen Kurven sind im folgenden Diagramm dargestellt.

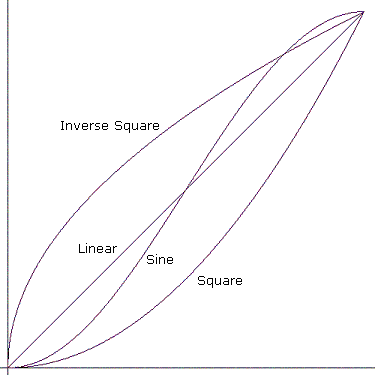
Parameterkurven

Mathematisch funktionieren die Kurven wie folgt. Angenommen, eine Kurve beginnt zum Zeitpunkt t₀ mit dem Wert v₀ und endet zum Zeitpunkt t₁ mit dem Wert v₁. Die beiden Punkte, die die Kurve definieren, sind (t₀, v₀) und (t₁, v₁).

  • Δt die Gesamtdauer der Kurve, t₁–t₀.
  • Δv ist das Intervall zwischen den Anfangs- und Endwerten v₁–v₀.
  • Jederzeit t so, dass t₀ <= t<= t₁, let Δt' = t–t₀.

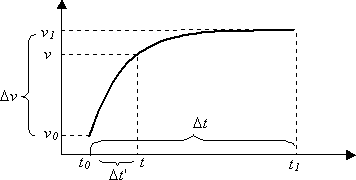
Parameterberechnung

Der Wert des Parameters zum Zeitpunkt t lautet:

v = f( Δt' / Δt ) * Δv + v₀

wobei f(x) eine Funktion ist, die vom Kurventyp bestimmt wird:

  • Linear: y = x
  • Quadrat: y = x^2
  • Umgekehrtes Quadrat: y = sqrt(x)
  • Sinus: y = [ sin(πx – π/2) + 1 ] / 2

Beachten Sie, dass Δt' < Δt, sodass der Begriff Δt'/Δt zwischen 0 und 1 liegt. Daher liegt f(x) auch zwischen 0 und 1, und v liegt immer zwischen v₀ und v₁. Dies gilt unabhängig davon<, ob v₀ v₁ oder umgekehrt. Anders ausgedrückt: Die Kurve wird durch das Rechteck (t₀, v₀, t₁, v₁) begrenzt.

Für die Sinuskurve reicht der Wert von (πx – π/2) von –π/2 bis π/2, was bedeutet, dass sin(πx – π/2) von –1 bis 1 liegt. Das Ergebnis wird dann normalisiert, sodass f(x) in den Bereich (0–1) fällt.

Medienparameter