PRT-Gleichungen (Direct3D 9)
Um einen Shader vollständig zu verstehen, der PRT implementiert, ist es nützlich, die Formel abzuleiten, die der Shader zum Berechnen der Exitradianz verwendet.
Zunächst ist die folgende Gleichung die allgemeine Gleichung zum Berechnen der Austrittsstrahlung, die sich aus direkter Beleuchtung eines diffusen Objekts mit beliebiger Fernbeleuchtung ergibt.
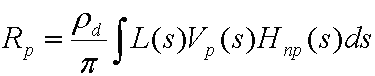
Dabei gilt Folgendes:
| Parameter | BESCHREIBUNG |
|---|---|
| Rp | Die Ausgangsstrahlung am Scheitelpunkt p. Wird an jedem Scheitelpunkt auf dem Gitter ausgewertet. |
| pd | Die Albedo der Oberfläche. |
| pi | Eine Konstante, die als Energieeinsparungsnormalisierungsfaktor verwendet wird. |
| L(s) | Die Lichtumgebung (Quellstrahl). |
| Vp₍s₎ | Eine binäre Sichtbarkeitsfunktion für Punkt p. Es ist 1, wenn der Punkt das Licht sehen kann, 0, wenn nicht. |
| Hnp₍s₎ | Der Kosinusbegriff aus Lamberts Gesetz. Gleich max((Np· s), 0), wobei Np die Oberfläche normal am Punkt p ist. |
| s | Die Variable, die über die Kugel integriert wird. |
Mithilfe von sphärischen Basisfunktionen, z. B. sphärischen Oberschwingungen, wird mit der folgenden Gleichung die Beleuchtungsumgebung ungefährt.
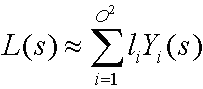
Dabei gilt Folgendes:
| Parameter | BESCHREIBUNG |
|---|---|
| L(s) | Die Lichtumgebung (Quellstrahl). |
| i | Eine ganze Zahl, die über die Anzahl der Basisfunktionen summiert. |
| O | Die Reihenfolge der sphärischen Oberschwingungen. |
| li | Ein Koeffizienten. |
| Yi(s) | Eine Basisfunktion über der Sphäre. |
Die Sammlung dieser Koeffizienten, L', liefert die optimale Näherung für Funktion L(s) mit den Basisfunktionen Y(s). Das Ersetzen und Verteilen ergibt die folgende Gleichung.
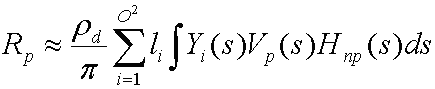
Das Integral von Yi(s)Vp₍s₎Hnp₍s₎ ist ein Transferkoeffizienten tpi , den der Simulator für jeden Scheitelpunkt auf dem Netz vorkompiliert. Wenn Sie diese ersetzen, ergibt sich die folgende Gleichung.
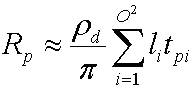
Wenn Sie dies in Vektornotation ändern, wird die folgende unkomprimierte Gleichung zum Berechnen der Ausgangsstrahlung für jeden Kanal ergibt.
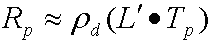
Dabei gilt Folgendes:
| Parameter | BESCHREIBUNG |
|---|---|
| Rp | Die Ausgangsstrahlung am Scheitelpunkt p. |
| pd | Die Albedo der Oberfläche. |
| L' | Der Vektor von li, und ist die Projektion der Quellstrahlung in die sphärischen harmonischen Basisfunktionen. Dies ist ein Ordnungsvektor² von kugelförmigen harmonischen Koeffizienten. |
| Tp | Ein Order²-Übertragungsvektor für Vertex p. Der Simulator dividiert die Übertragungskoeffizienten durch p. |
Beide Vektoren sind ein Order²-Vektor von kugelförmigen harmonischen Koeffizienten. Beachten Sie also, dass dies einfach ein Punktprodukt ist. Je nach Reihenfolge kann der Punkt teuer sein, sodass eine Komprimierung verwendet werden kann. Ein Algorithmus namens Clustered Principal Component Analysis (CPCA) komprimiert die Daten effizient. Dies ermöglicht die Verwendung einer höhergeordneten, kugelförmigen harmonischen Näherung, die zu schärferen Schatten führt.
CPCA stellt die folgende Gleichung bereit, um den Übertragungsvektor zu nähern.
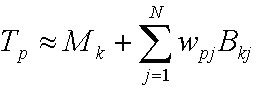
Dabei gilt Folgendes:
| Parameter | BESCHREIBUNG |
|---|---|
| Tp | Der Übertragungsvektor für Scheitelpunkt p. |
| Mk | Der Mittelwert für Cluster k. |
| j | Eine ganze Zahl, die über die Anzahl der PCA-Vektoren summiert. |
| N | Die Anzahl der PCA-Vektoren. |
| wpj | Die jth PCA-Gewichtung für Punkt p. |
| Bkj | Der jth PCA-Basisvektor für cluster k. |
Ein Cluster besteht einfach aus einer Reihe von Scheitelpunkten, die denselben mittleren Vektor verwenden. Im Folgenden wird erläutert, wie Sie den Clustermittelwert, die PCA-Gewichtungen, die PCA-Basisvektoren und die Cluster-IDs für die Scheitelpunkte abrufen.
Das Ersetzen dieser beiden Formeln ergibt Folgendes:
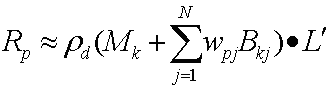
Die Verteilung des Punktprodukts ergibt dann die folgende Gleichung.
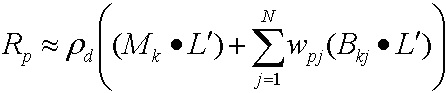
Weil beide (Mk· L') und (Bkj· L') sind konstant pro Scheitelpunkt, die Stichprobe berechnet diese Werte mit der CPU und übergibt sie als Konstanten an den Vertexshader; Da sich wpj für jeden Scheitelpunkt ändert, speichert das Beispiel diese Daten pro Scheitelpunkt im Vertexpuffer.
Zugehörige Themen