Vektoren, Scheitelpunkte und Quaternionen

In Direct3D beschreiben Scheitelpunkte die Position und Ausrichtung. Jeder Scheitelpunkt in einem Grundtyp wird durch einen Vektor beschrieben, der seine Position, Farbe, Texturkoordinaten und einen normalen Vektor angibt, der seine Ausrichtung angibt.

Quaternions fügen ein viertes Element zu den Werten [x, y, z] hinzu, die einen Vektor mit drei Komponenten definieren. Quaternionen sind eine Alternative zu den Matrixmethoden, die in der Regel für 3D-Drehungen verwendet werden. Eine Quaternion stellt eine Achse in einem 3D-Raum und eine Rotation um diese Achse dar. Beispielsweise kann eine Quaternion eine Achse (1,1,2) und eine Drehung von 1 Bogenmaß darstellen. Quaternionen tragen wertvolle Informationen, aber ihre wahre Kraft kommt aus den beiden Operationen, die Sie ausführen können: Zusammensetzung und Interpolation.

Die Komposition auf Quaternionen ist vergleichbar mit der Kombination. Die Zusammensetzung von zwei Quaternionen wird wie in der folgenden Abbildung notiert.

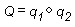
Die Zusammensetzung von zwei Quaternionen, die auf eine Geometrie angewendet werden, bedeutet: "Drehen sie die Geometrie um die Achse durch Drehung₁, und drehen Sie sie dann um die Achse₁." In diesem Fall stellt Q eine Drehung um eine einzelne Achse dar, die das Ergebnis des Anwendens von q₁ auf die Geometrie ist.

Mithilfe der Quaternion-Interpolation kann eine Anwendung einen reibungslosen und vernünftigen Pfad von einer Achse und Ausrichtung zu einer anderen berechnen. Daher bietet die Interpolation zwischen q₁ und q² eine einfache Möglichkeit, von einer Ausrichtung zur anderen zu animieren.

Wenn Sie Die Komposition und Interpolation zusammen verwenden, bieten sie ihnen eine einfache Möglichkeit, eine Geometrie so zu bearbeiten, dass sie komplex erscheint. Angenommen, Sie haben eine Geometrie, die Sie in eine bestimmte Ausrichtung drehen möchten. Sie wissen, dass Sie ihn um die Achse herum drehen möchten, dann um die Achse r₁ Grad um die Achse herum drehen möchten₁, aber Sie wissen nicht, dass die endgültige Quaternion. Mithilfe der Komposition können Sie die beiden Drehungen der Geometrie kombinieren, um eine einzelne Quaternion zu erhalten, die das Ergebnis ist. Dann könnten Sie zwischen dem Original und dem zusammengesetzten Quaternion interpolieren, um einen reibungslosen Übergang von einem zum anderen zu erzielen.

Verwandte Themen

Koordinatensysteme und Geometrie