Freigeben über

Geräteausrichtung – Quaternionenvektor-Algorithmus

  • Artikel

In diesem Artikel wird der Algorithmus beschrieben, der vom Windows Hardware Lab Kit (Windows HLK) verwendet wird, um den Deltawert zwischen dem empfangenen und dem erwarteten Vektor für die neunachsige Datengenauigkeit in den erweiterten Tests für Ausrichtungssensoren zu bestimmen. Bei den Tests wird überprüft, ob die Sensorfusion ordnungsgemäß integriert ist und ob alle für die Sensorfusion erforderlichen Sensoren ordnungsgemäß integriert und installiert sind.

Hinweis

In bestimmten Fällen können Sie das Sensordiagnosetool verwenden, um den 3D-Neigungssensor und den aggregierten Geräteausrichtungssensor zu untersuchen, der getestet wird.

Quaternionenvektor-Algorithmus

Der Algorithmus verwendet den Arcuscosinus des vierdimensionalen Punktprodukts der beiden Vektoren, geteilt durch das Produkt des Betrags der beiden Vektoren und geteilt durch 2. Dieser Algorithmus ist in Abbildung 1 (Formel des Quaternionenvektor-Algorithmus) zu sehen:

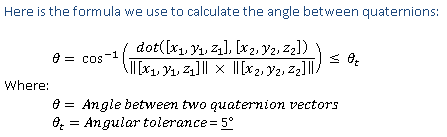
Formel des Quaternionenvektor-Algorithmus

Rotationsmatrixwerte werden für die Genauigkeitsüberprüfung in Quaternionenwerte konvertiert. Der berechnete Quaternionenvektor sollte nicht mehr als +/-5 Grad vom erwarteten Quaternionenvektor abweichen (Toleranz gegenüber Winkeln zwischen Quaternionenvektoren). (**+/-10 Grad Genauigkeit bei Richtungsachse zulässig.) Der Windows HLK-Test erlaubt für Øt einen Deltawert von bis zu 15 Grad.

Berechnen des Deltawinkels zwischen den empfangenen und erwarteten Quaternionenvektoren

In diesem Abschnitt wird die Berechnung des Deltawinkels zwischen den empfangenen und erwarteten Quaternionenvektoren in erweiterten Ausrichtungstests des Windows HLK beschrieben.

Im Datenbericht des aggregierten Geräteausrichtungssensors sind die beiden folgenden Datenwerte relevant:

  • Quaternionenvektor

  • Rotationsmatrix

Der Test umfasst die beiden folgenden Überprüfungen:

  1. Überprüfung des empfangenen Quaternionenvektors aus dem Sensordatenbericht. Ein Quaternionenvektor hat das Format (xi + yj + zk + w).

    1. Für w wird immer ein positiver Wert erwartet.

    2. Der Quaternionenvektor muss normalisiert und ungleich 0 sein. Der Betrag des Vektors muss nahe 1,0 sein. Für Rundungsfehler bei der Berechnung des Betrags wird ein Spielraum von einem Prozent eingeräumt.

    3. Der Deltawinkel wird mithilfe folgender Formel berechnet delta = 2 · Acos( ( Exp . Rec ) / ( | Exp | · | Rec | ) ). Hierbei gilt:

      \* gibt eine skalare Multiplikation an.

      . gibt ein Punktprodukt an.

      Exp ist der erwartete Quaternionenvektor.

      Rec ist der empfangene Quaternionenvektor.

      | Q | gibt den Betrag des Quaternionenvektors an.

      delta ist der Winkel in Grad.

    4. Ist der Deltawert größer als 360 Grad, wird er als delta = delta - 360 neu berechnet.

    5. An diesem Punkt sollte der Deltawert kleiner oder gleich der Fehlertoleranz (beispielsweise 10 Grad) sein.

  2. Überprüfung der empfangenen Rotationsmatrix. Als Rotationsmatrix wird eine 3x3-Matrix erwartet.

    1. Jeder Spalten- und Zeilenvektor der Rotationsmatrix muss normalisiert und ungleich 0 sein. Für Rundungsfehler bei der Berechnung des Betrags wird ein Spielraum von einem Prozent eingeräumt.

    2. Die empfangene Rotationsmatrix wird in einen Quaternionenvektor umgewandelt.

    3. Alle Schritte von <a> bis <e> der Überprüfung (1) werden erneut verwendet.

Testen der Sensorfunktionalität mit dem Sensordiagnosetool

Integrieren von Bewegungs- und Ausrichtungssensoren