Codemetriken – Zyklomatische Komplexität
Bei der Arbeit mit Codemetriken scheint eines der am wenigsten verstandenen Elemente eine zyklomatische Komplexität zu sein. Im Wesentlichen sind höhere Zahlen mit zyklomatischer Komplexität schlecht und niedrigere Zahlen sind gut. Sie können die zyklomatische Komplexität verwenden, um einen Eindruck davon zu erhalten, wie schwierig ein gegebener Code sein könnte, um Fehler zu testen, zu verwalten oder zu beheben sowie einen Hinweis darauf, wie wahrscheinlich der Code sein wird, Fehler zu erzeugen. Auf hoher Ebene bestimmen wir den Wert der zyklomatischen Komplexität, indem wir die Anzahl der entscheidungen zählen, die in Ihrem Quellcode getroffen wurden. In diesem Artikel beginnen Sie mit einem einfachen Beispiel für die zyklomatische Komplexität, um das Konzept schnell zu verstehen, und sehen Sie sich dann einige zusätzliche Informationen zur tatsächlichen Nutzung und vorgeschlagenen Grenzwerten an. Schließlich gibt es einen Abschnitt mit Zitaten, die verwendet werden können, um tiefer in dieses Thema einzutauchen.
Beispiel
Die zyklomatische Komplexität wird als Messung der "Menge der Entscheidungslogik in einer Quellcodefunktion" NIST235definiert. Einfach gesagt, je mehr Entscheidungen im Code getroffen werden müssen, desto komplexer ist es.
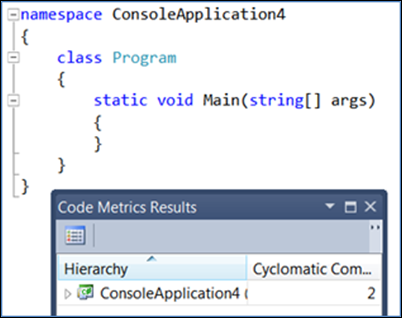
Sehen wir es in Aktion. Erstellen Sie eine neue Konsolenanwendung, und berechnen Sie sofort Ihre Codemetriken, indem Sie Analysieren > Codemetrik für Projektmappe berechnen auswählen.
 )
)
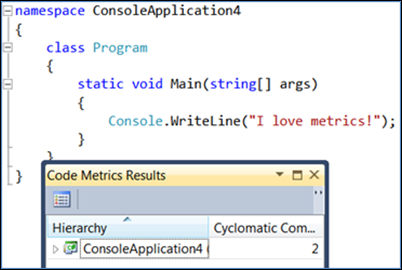
Beachten Sie, dass die zyklomatische Komplexität bei 2 liegt (der niedrigste mögliche Wert). Wenn Sie Nicht-Entscheidungscode hinzufügen, beachten Sie, dass sich die Komplexität nicht ändert:
 )
)
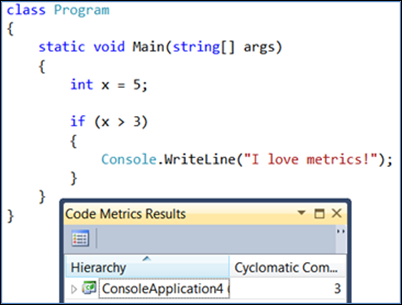
Wenn Sie eine Entscheidung hinzufügen, geht der Wert für die zyklomatische Komplexität um eins hoch:
 )
)
Wenn Sie die If-Anweisung in eine Switch-Anweisung mit vier entscheidungen ändern, geht es von den ursprünglichen zwei bis sechs:
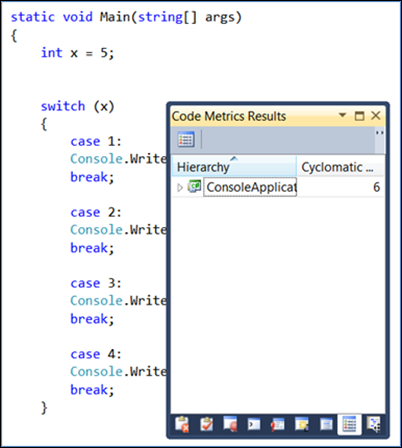
Werfen wir einen Blick auf eine (hypothetische) größere Codebasis.
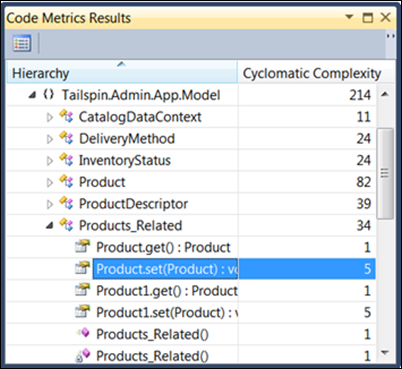
Beachten Sie, dass die meisten Elemente, wenn Sie einen Drilldown in die Products_Related-Klasse ausführen, einen Wert von eins haben, aber ein paar davon haben eine Komplexität von fünf. Allein dieser Unterschied könnte nicht groß sein, aber angesichts der Tatsache, dass die meisten anderen Mitglieder eine in derselben Klasse haben, sollten Sie sich auf jeden Fall näher mit diesen beiden Elementen befassen und sehen, was in ihnen ist. Sie können einen genaueren Blick darauf werfen, indem Sie mit der rechten Maustaste auf das Element klicken und im Kontextmenü "Zum Quellcode wechseln" auswählen. Werfen Sie einen genaueren Blick auf Product.set(Product):
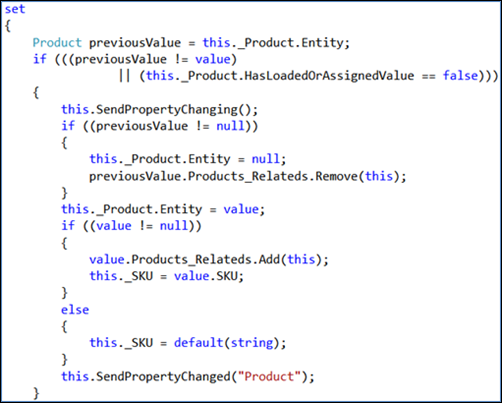
Angesichts aller If-Aussagen können Sie sehen, warum die zyklomatische Komplexität bei fünf liegt. An diesem Punkt können Sie entscheiden, dass dieses Ergebnis ein akzeptables Maß an Komplexität ist, oder Sie können umgestalten, um die Komplexität zu verringern.
Die Magische Zahl
Wie bei vielen Metriken in dieser Branche gibt es keine genaue zyklomatische Komplexitätsgrenze, die allen Organisationen entspricht. NIST235 weist jedoch darauf hin, dass ein Grenzwert von 10 ein guter Ausgangspunkt ist:
"Die genaue Zahl, die als Grenze verwendet werden soll, bleibt jedoch etwas umstritten. Die ursprüngliche Grenze von 10, wie von McCabe vorgeschlagen, hat erhebliche unterstützende Beweise, aber Grenzwerte, die so hoch wie 15 sind, wurden ebenfalls erfolgreich verwendet. Grenzwerte von mehr als 10 sollten für Projekte reserviert werden, die mehrere operative Vorteile gegenüber typischen Projekten haben, z. B. erfahrene Mitarbeiter, formales Design, eine moderne Programmiersprache, strukturierte Programmierung, Code-Durchsprachen und einen umfassenden Testplan. Mit anderen Worten, eine Organisation kann eine Komplexitätsgrenze von mehr als 10 auswählen, aber nur, wenn sie sicher ist, was sie tut und bereit ist, den zusätzlichen Testaufwand zu widmen, der von komplexeren Modulen benötigt wird." NIST235
Zyklomatische Komplexität und Zeilennummern
Nur die Anzahl der Codezeilen selbst zu betrachten, ist am besten ein sehr breiter Prädiktor der Codequalität. Es gibt einige grundlegende Wahrheiten für die Idee, dass je mehr Codezeilen in einer Funktion, desto wahrscheinlicher ist es, Fehler zu haben. Wenn Sie jedoch zyklomatische Komplexität mit Codezeilen kombinieren, haben Sie ein viel klareres Bild des Fehlerpotenzials.
Wie vom Software Assurance Technology Center (SATC) bei der NASA beschrieben:
"Die SATC hat festgestellt, dass die effektivste Bewertung eine Kombination aus Größe und (Zyklomatischer) Komplexität ist. Die Module mit einer hohen Komplexität und einer großen Größe neigen dazu, die niedrigste Zuverlässigkeit zu haben. Module mit geringer Größe und hoher Komplexität stellen ebenfalls ein Zuverlässigkeitsrisiko dar, da sie tendenziell sehr knapper Code sind, der schwer zu ändern oder zu modifizieren ist." SATC-
Codeanalyse
Die Codeanalyse enthält eine Kategorie von Maintainability-Regeln. Weitere Informationen finden Sie unter Wartbarkeitsregeln. Bei Verwendung der Legacy-Code-Analyse enthält der Regelsatz "Erweiterte Entwurfsrichtlinie" einen Wartbarkeitsbereich.
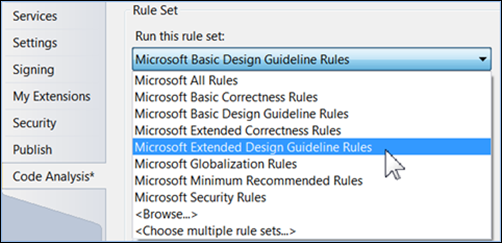
Im Bereich der Wartbarkeit gibt es eine Regel für Komplexität.

Diese Regel gibt eine Warnung aus, wenn die zyklomatische Komplexität 25 erreicht, damit Sie übermäßige Komplexität vermeiden können. Weitere Informationen zur Regel finden Sie unter CA1502-
Alles zusammensetzen
Die Grundlinie besteht darin, dass eine hohe Komplexitätszahl eine höhere Wahrscheinlichkeit von Fehlern mit erhöhter Zeit zur Wartung und Problembehandlung bedeutet. Werfen Sie einen genaueren Blick auf alle Funktionen, die eine hohe Komplexität aufweisen, und entscheiden Sie, ob sie umgestaltet werden sollen, um sie weniger komplex zu machen.
Zitate
MCCABE5
McCabe, T. und A. Watson (1994), Software Complexity (CrossTalk: The Journal of Defense Software Engineering).
NIST235
Watson, A. H., & McCabe, T. J. (1996). Strukturierte Tests: Eine Testmethodik mit der zyklomatischen Komplexitätsmetrik (NIST Special Publication 500-235). Abgerufen am 14. Mai 2011 von der McCabe Software-Website: http://www.mccabe.com/pdf/mccabe-nist235r.pdf
SATC
Rosenberg, L., Hammer, T., Shaw, J. (1998). Softwaremetriken und Zuverlässigkeit (Proceedings of IEEE International Symposium on Software Reliability Engineering). Abgerufen am 14. Mai 2011 von der Website der Penn State University: https://citeseerx.ist.psu.edu/pdf/31e3f5732a7af3aecd364b6cc2a85d9495b5c159