Polynomiale Regression
Bisher haben wir uns nur Modelle für die lineare Regression angesehen, also Modelle, die in Form von geraden Linien modelliert werden können. Für Regressionsmodelle können aber nahezu alle anderen Arten von Beziehungen genutzt werden.
Was ist die polynomiale Regression?
Bei der polynomialen Regression werden Beziehungen als besonderer Kurventyp modelliert. Bei Polynomen handelt es sich um eine Familie von Kurven, die von einfachen bis zu komplexen Formen reichen. Je mehr Parameter die Gleichung (Modell) enthält, desto komplexer kann die Kurve sein.
Ein Polynom mit zwei Parametern führt beispielsweise nur zu einer geraden Linie:
y = Achsenabschnitt + B1 · x
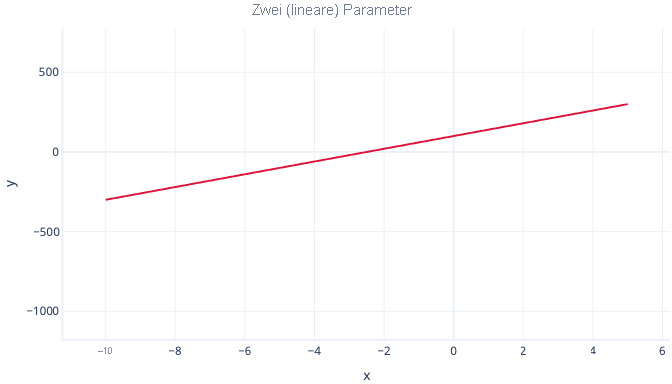
Ein Polynom mit drei Parametern weist dagegen nur einen Bogen auf:
y = Achsenabschnitt + B1 · x + B2 · x2
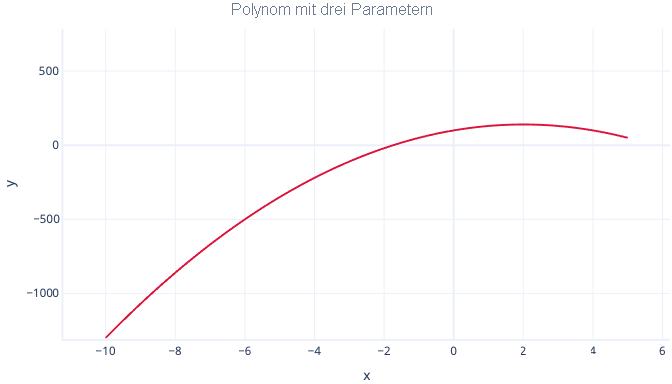
Ein Polynom mit vier Parametern kann zwei Bögen aufweisen:
y = Achsenabschnitt + B1 · x + B2 · x2 + B3 · x3
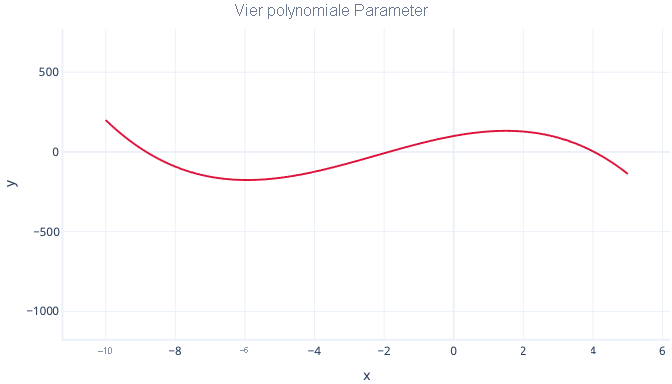
Vergleich: Polynome und andere Kurven
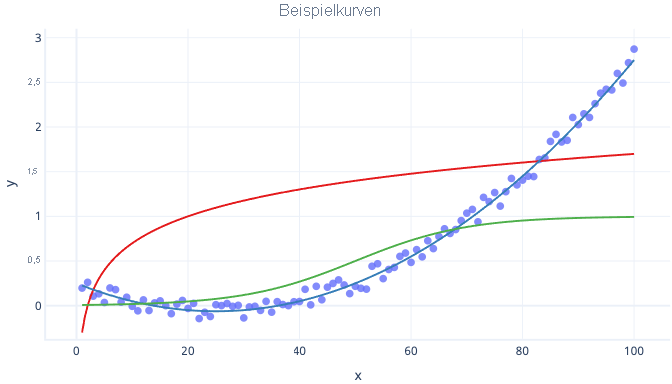
Es gibt viele Arten von Kurven, z. B. logarithmische Kurven und logistische (S-förmige) Kurven, die alle bei der Regression genutzt werden können.
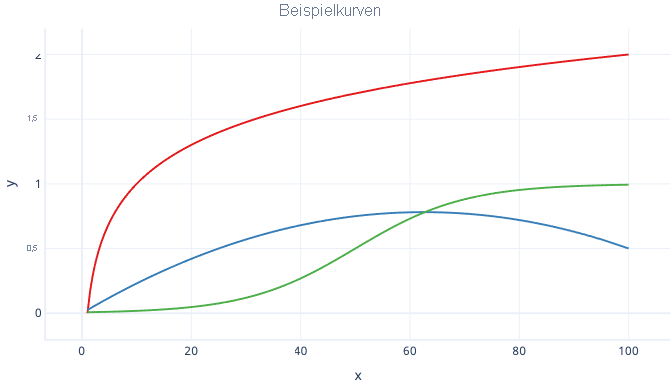
Ein wesentlicher Vorteil der Polynomregression ist, dass Sie damit die unterschiedlichsten Arten von Beziehungen untersuchen können. Beispielsweise können Sie die Polynomregression für Beziehungen verwenden, die innerhalb eines bestimmten Bereichs von Featurewerten negativ, innerhalb anderer Bereiche aber positiv sind. Sie können sie auch dann verwenden, wenn für die Bezeichnung (y-Wert) keine theoretische Obergrenze gilt.
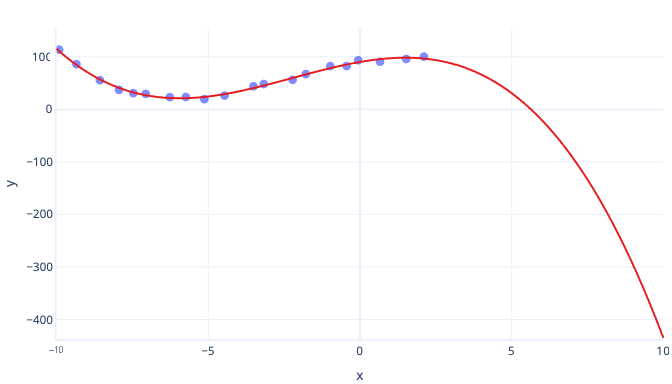
Der Hauptnachteil von polynomialen Kurven ist, dass sie häufig nicht gut extrapoliert werden können. Anders ausgedrückt: Wenn wir versuchen, Werte vorherzusagen, die größer oder kleiner als unsere Trainingsdaten sind, können auf Polynomen basierende Vorhersagen zu unrealistisch extremen Werten führen. Ein weiterer Nachteil ist, dass es bei Polynomkurven leicht zu einer Überanpassung kommen kann. Dies bedeutet, dass durch Rauschen in den Daten die Form der Kurve wesentlich stärker als bei einfacheren Modellen, z. B. der einfachen linearen Regression, verändert werden kann.
Können Kurven mit mehreren Merkmalen verwendet werden?
Wir haben gesehen, wie bei der multiplen Regressionen mehrere lineare Beziehungen gleichzeitig angepasst werden können. Es ist aber nicht erforderlich, dies auf lineare Beziehungen zu beschränken. Für diese Beziehungen können Kurven aller Art verwendet werden, sofern dies eine passende Lösung darstellt. Sie sollten aber darauf achten, dass Sie keine Kurven, z. B. Polynome, mit mehreren Features verwenden, wenn dies nicht erforderlich ist. Der Grund ist, dass die Beziehungen hierbei sehr komplex werden können. Dies erschwert das Verständnis der Modelle sowie die Bewertung, ob sie zu Vorhersagen führen, die aus realer Sicht keinen Sinn ergeben.