Vergleichen und Optimieren von ROC-Kurven
Mithilfe von ROC-Kurven (Grenzwertoptimierungskurven) können Sie Modelle miteinander vergleichen und ein ausgewähltes Modell optimieren. Im Folgenden wird erläutert, wie und warum dies durchgeführt wird.
Optimieren eines Modells
Die offensichtlichste Grund für eine ROC-Kurve ist die Auswahl des Entscheidungsschwellenwerts, der die beste Leistung bietet. Denken Sie daran, dass das Modell Ihnen Wahrscheinlichkeiten liefert, zum Beispiel die Wahrscheinlichkeit von 65 %, dass es sich bei der Stichprobe um einen Wanderer handelt. Der Entscheidungsschwellenwert ist der Punkt, über dem eine Stichprobe als „true“ (Wanderer) und unter dem sie als false (Baum) klassifiziert wird. Wenn der Entscheidungsschwellenwert bei 50 % liegt, würde bei 65 % der Wert "true" (Wanderer*in) zugewiesen werden. Wenn der Entscheidungsschwellenwert jedoch bei 70 % liegt, wäre eine Wahrscheinlichkeit von 65 % zu gering, und der Wert "false" (Baum) würde zugewiesen werden.
Sie haben in der vorherigen Übung gelernt, dass Sie beim Erstellen einer ROC-Kurve nur den Entscheidungsschwellenwert ändern und dann bewerten, wie gut das Modell funktioniert. So können Sie den Schwellenwert ermitteln, der die optimalen Ergebnisse liefert.
Es gibt keinen festen Schwellenwert, der zur bestmöglichen True-Positive-Rate (TPR) und zur geringstmöglichen False-Positive-Rate (FPR) führt. Der optimale Schwellenwert hängt also davon ab, was Sie erreichen möchten. In diesem Szenario ist eine hohe True-Positive-Rate beispielsweise besonders wichtig, denn wenn Wandernde nicht richtig erkannt werden, weiß das Team im Fall einer Lawine nicht, dass sie gerettet werden müssen. Wenn die False-Positive-Rate jedoch zu hoch ist, wird das Rettungsteam wiederholt ausgesendet, obwohl keine Menschen gerettet werden müssen. In anderen Situationen wird die False-Positive-Rate als wichtiger betrachtet. In der Wissenschaft gilt beispielsweise eine niedrige Toleranzschwelle für falsch positive Ergebnisse. Wenn die False-Positive-Rate für wissenschaftliche Experimente zu hoch wäre, gäbe es unendlich viele widersprüchliche Behauptungen. So könnte nicht festgestellt werden, welche davon brauchbar sind.
Vergleichen von Modellen mit AUC
Sie können ROC-Kurven genau wie Kostenfunktionen dazu verwenden, Modelle miteinander zu vergleichen. Eine ROC-Kurve für ein Modell zeigt, wie gut es für verschiedene Entscheidungsschwellenwerten funktioniert. Letztendlich ist bei einem Modell entscheidend, wie es in der Praxis mit nur einem Entscheidungsschwellenwert funktioniert. Warum werden Modelle dann anhand von Schwellenwerten verglichen, die nie verwendet werden? Auf diese Frage gibt es zwei Antworten.
Erstens entspricht der Vergleich von ROC-Kurven auf bestimmte Weise der Durchführung eines statistischen Tests, aus dem nicht nur hervorgeht, dass ein Modell für diesen bestimmten Testdatensatz besser funktioniert hat, sondern auch, wie wahrscheinlich es auch weiterhin auf diese Weise funktioniert. Das ist nicht Bestandteil dieses Lernmaterial, doch Sie sollten es im Hinterkopf behalten.
Zweitens zeigt die ROC-Kurve zu einem gewissen Grad auf, wie stark das Modell auf einen perfekten Schwellenwert angewiesen ist. Wenn Ihr Modell beispielsweise nur gut funktioniert, wenn ein Entscheidungsschwellenwert von 0,9 vorliegt, aber der tatsächliche Wert deutlich darüber oder darunter liegt, besteht noch Optimierungsbedarf. Sie bevorzugen wahrscheinlich die Arbeit mit einem Modell, das mit verschiedenen Schwellenwerten gut funktioniert. So bleibt die Modellleistung erhalten, auch wenn sich die Daten aus der Praxis geringfügig von den Testdatensätzen unterscheiden.
Vergleichen von ROC-Kurven
ROC-Kurven können am einfachsten anhand der Fläche unter der Kurve (AUC, Area Under Curve) verglichen werden. Dabei handelt es sich wie der Begriff verrät um den Bereich, der unter der Kurve liegt. Beispielsweise weist das perfekte Modell aus der letzten Übung eine AUC von 1 auf:
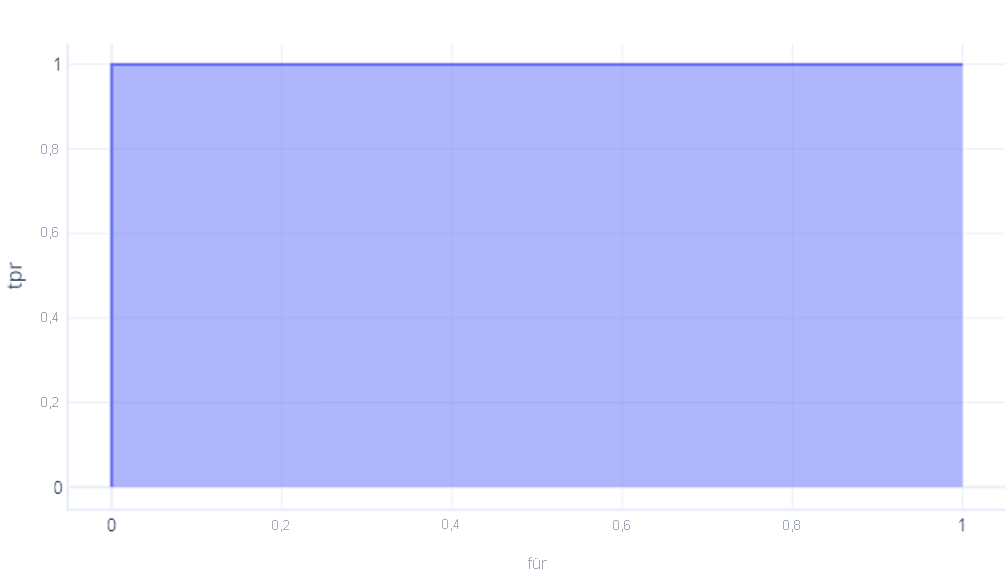
Im Vergleich dazu hat das Modell, das nur zufällig richtig lag, eine Fläche von etwa 0,5:
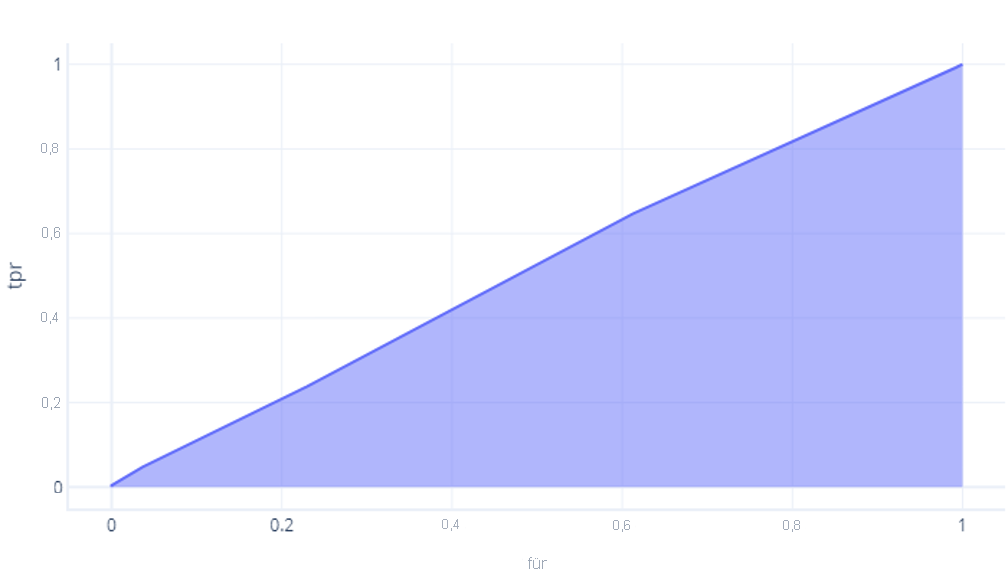
Je perfekter ein Modell ist, desto größer wird diese Fläche. Wenn ein Modell eine große AUC aufweist, wissen Sie, dass es mit verschiedenen Schwellenwerten funktioniert. Das lässt auf eine gute Architektur und ein gutes Training schließen. Im Gegensatz dazu funktioniert ein Modell mit einer kleinen AUC (näher an 0,5) nicht gut.