Was ist Superposition im Quantencomputing?

  • 5 Minuten

Wenn die Katze aus der vorherigen Einheit eine Quantenkatze war, wäre der Zustand der Quantenkatze und des Kastensystems identisch: die Summe der sechs verschiedenen Positionen der Quantenkatze in Bezug auf den Kasten, gewichtet nach der Wahrscheinlichkeit, die Quantenkatze in dieser Position zu finden. Der einzige Unterschied besteht darin, dass die klassische Katze an einer (und nur einer) von sechs möglichen Positionen sein kann, während die Quantenkatze gleichzeitig an allen sechs Positionen sein kann!

In der klassischen Welt können Objekte nur jeweils in einem Zustand sein. In der klassischen Welt können sich Objekte immer nur in einem Zustand befinden. Dieses Phänomen wird als Superposition bezeichnet.

Im Quantencomputing nutzt (leider) niemand Quantenkatzen, sondern Qubits. Das Wort „Qubit“ bedeutet „Quantenbit“. Genau wie bei der klassischen Berechnung, bei der die Grundeinheit der Informationen das Bit ist, ist beim Quantencomputing die Basiseinheit der Informationen das Qubit. Und genau wie das Bit zwei mögliche Werte annehmen kann, 0 und 1, ist ein Qubit jedes Quantenteilchen, das in zwei möglichen Zustände haben kann. Beispielsweise könnte ein Qubit ein Photon sein, das in zwei Richtungen polarisiert werden kann, oder ein Elektron, das zwei Energiestufen aufweisen kann.

Wie können Sie die Superposition in einem Qubit darstellen? Wie hoch ist die Wahrscheinlichkeit, ein Qubit in einem bestimmten Zustand zu finden?

Wie können Sie die Superposition in einem Qubit darstellen?

Ein Qubit ist ein Quantenteilchen, das zwei mögliche Positionen oder Zustände hat. Analog zum klassischen Bit werden die Quantenzustände eines Qubit auch als $0$ und $1$ bezeichnet. Ein Qubit kann sich im Zustand $0$, im Zustand $1$ und in jeder Superposition der beiden Zustände befinden. Wie können Sie diese Superposition darstellen?

Stellen Sie sich vor, Sie zeichnen einen Kreis und eine vertikale und horizontale Achse so, dass der Schnittpunkt der Achsen in der Mitte des Kreises liegt. Der Zustand $0$ wird am oberen Punkt der vertikalen Achse und der Zustand $1$ am unteren Punkt platziert.

Wie lässt sich diese Darstellung beschreiben? Sie könnten sagen, dass der Zustand $0$ ein Pfeil bzw. ein Vektor ist, der nach oben zeigt, und der Zustand $1$ ein Vektor, der nach unten zeigt. Daher ist ein klassisches Bit ein Vektor, der entweder nach oben oder unten, aber nie in eine andere Richtung zeigt.

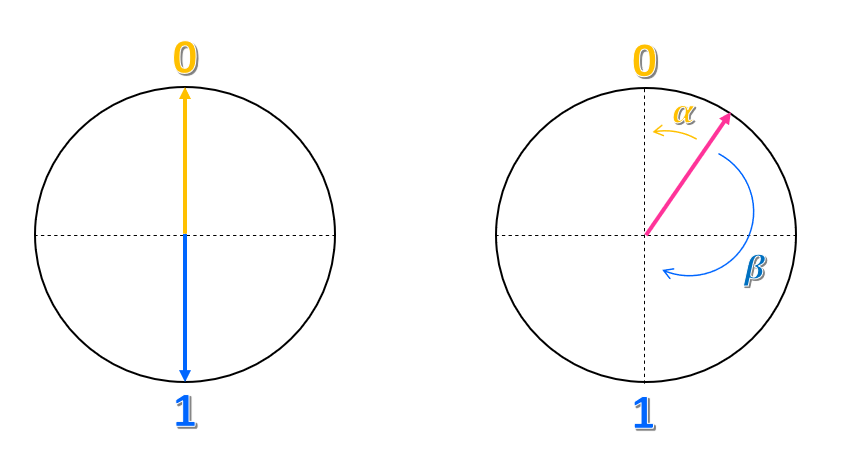
Diagramm: Kreis mit zwei Pfeilen, die vom Mittelpunkt des Kreises nach oben und unten zeigen Die Pfeile stellen die Zustände 0 bzw. 1 dar. Jeder andere Zustand ist ein Pfeil, der in andere Richtungen zeigt.

Was ist mit einem anderen Punkt des Kreises? Wie können Sie diesen Zustand darstellen? Genauso wie Koordinaten in einer Ebene können Sie versuchen, ihn als Kombination aus den beiden Zuständen $0$ und $1$ darzustellen. Sie können beispielsweise den Abstand des Vektors vom Zustand $0$ nehmen und diesen Winkel „$\alpha$“ nennen. Dann nehmen Sie den Abstand vom Zustand $1$ und nennen diesen Winkel „$\beta$“. Sie können den Zustand als „$\alpha 0 + \beta 1 $“ darstellen. Daher ist der Zustand eine Superposition der Zustände $0$ und $1$.

Wie im Beispiel mit der Katze und der Box ist der globale Zustand eines Qubit die Summe der einzelnen Zustände $0$ und $1$, gewichtet nach der Wahrscheinlichkeit, das Qubit in diesem Zustand zu finden („$\alpha$“ und „$\beta $“).

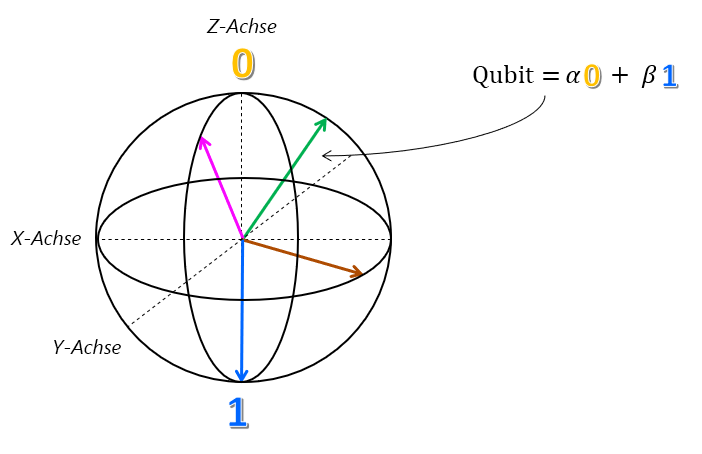
Diagramm: Bloch-Kugel mit den Zuständen 0 und 1 auf der Z-Achse und einem anderen Vektor, der die unendlichen Kombinationen von Superpositionen darstellt

Diese Darstellung eines Qubit ist tatsächlich genau und wird als Bloch-Kugel bezeichnet.

Tipp

Die Bloch-Kugel ist ein leistungsfähiges Werkzeug, da die Vorgänge, die wir für ein Qubit ausführen können, als Drehungen um eine der Kardinalachsen dargestellt werden können. Während die Vorstellung einer Quantenberechnung als eine Folge von Rotationen eine mächtige Intuition ist, ist es eine Herausforderung, diese Intuition zu nutzen, um Algorithmen zu entwerfen und zu beschreiben. Q# entschärft dieses Problem, indem eine Sprache zum Beschreiben solcher Drehungen bereitgestellt wird.

Wie hoch ist die Wahrscheinlichkeit, ein Qubit in einem Zustand zu finden?

Wie im Beispiel mit der Katze und der Box in der vorherigen Lektion ist der globale Zustand eines Qubit die Summe der einzelnen Zustände $0$ und $1$, gewichtet nach der Wahrscheinlichkeit, das Qubit in diesem Zustand zu finden („$\alpha$“ und „$\beta $“). Die Zahlen „$\alpha$“ und „$\beta$“ stellen dar, wie „nah“ der Qubit-Zustand den Zuständen $0$ bzw. $1$ ist. Geben also „$\alpha$“ und „$\beta$“ die Wahrscheinlichkeit an, das Qubit im Zustand $0$ oder $1$ zu finden? Nicht unbedingt.

Die Zahlen „$\alpha$“ und „$\beta$“ Wahrscheinlichkeitsamplituden für jeden Zustand. Die zugehörigen absoluten Werte – z. B. $|\alpha|^2$ – stellen die entsprechenden Wahrscheinlichkeiten dar. Die Wahrscheinlichkeit für die Beobachtung des Zustands $0$ ist etwa $|\alpha|^2$, und die Wahrscheinlichkeit für die Beobachtung des Zustands $1$ ist $|\Beta|^2$.

Die Zahlen $\alpha$ und $\beta$ können positive, negative oder sogar komplexe Zahlen sein. In einer gültigen Quantensuperposition müssen allerdings alle Wahrscheinlichkeiten die Summe 1 ergeben: $|\alpha|^2+|\beta|^2=1$. Diese Einschränkung wird als Normalisierungsbedingung bezeichnet. Sie können sich die Normalisierungsbedingung so vorstellen: Sie erhalten beim Messen immer ein Ergebnis, daher müssen sich die Wahrscheinlichkeiten der Messung jedes möglichen Ergebnisses immer zu 1 summieren.