Übung: Quantenverschränkung mit Q# erzeugen

7 Minuten

In der vorherigen Lektion haben Sie das Konzept der Quantenanglement- und Bell-Zustände kennengelernt.

Jetzt erstellen wir Quantenverschränkungen mithilfe von Q# und Azure Quantum Development Kit. Zum Erstellen einer Verschränkung müssen Sie zwei Quantenoperationen anwenden: das Hadamard-Gate und das Controlled-NOT (CNOT)-Gate.

Der Controlled-NOT-Vorgang (CNOT)

Wenn zwei Qubits verschränkt werden, hängt der Zustand eines Qubits vom Zustand des anderen Qubits ab. Um zwei Qubits zu verschränken, benötigen Sie daher einen Vorgang, der auf beide Qubits gleichzeitig wirkt. Dies wird als Multiqubit-Vorgang bezeichnet.

Um eine Quantenverschränkung zu erstellen, benötigen Sie den Multiqubit-Vorgang CNOT, der für Controlled-NOT steht. Bei diesem Vorgang werden zwei Qubits als Eingabe verwendet, eine fungiert als Steuerungsqubit und das andere ist der target Qubit. Der CNOT-Vorgang schaltet den Zustand des zweiten Qubits (des target-Qubits) ausschließlich dann um, wenn der Zustand des ersten Qubits (des Steuerungsqubits) $|1\rangle$ lautet.

Eingabe	Ausgabe
$\ket{00}$	$\ket{00}$
$\ket{01}$	$\ket{01}$
$\ket{10}$	$\ket{11}$
$\ket{11}$	$\ket{10}$

In Q# wirkt der CNOT Vorgang auf ein Array von zwei Qubits, und er schaltet den zweiten Qubit um, wenn der erste Qubit One ist.

Verschränkung mit einem CNOT-Vorgang

Durch Anwenden des Hadamard-Vorgangs, H, und des Controlled-NOT-Vorgangs, CNOT, können Sie zwei Qubits im Zustand $|00\rangle$ in den Bell-Zustand $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$ transformieren.

So funktioniert es:

Nehmen Sie zum Beispiel zwei Qubits mit dem Zustand $|00\rangle$. Der erste Qubit ist der Steuerungsqubit und der zweite Qubit ist der target Qubit.
Erstellen Sie durch Anwenden von $$H$ ein Superpositionszustand nur im Steuerungsqubit vor.

$$H |0_c\rangle=\frac{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)$$

Tipp

Die Indizes ${}_c$ and ${}_t$ geben die Steuerungs- und die target-Qubits an.
Wenden Sie den $CNOT-Operator$ auf das Steuerungsqubit an, das sich in einem Superpositionszustand befindet, und den target-Qubit, der sich im Zustand $|0_t\rangle$ befindet.

$$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c}+\ket{1_c})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}+|\ket{1_c 0_t})=$$$$=\frac{{1}{\sqrt2}(CNOT \ket{0_c 0_t} + CNOT \ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t}+\ket{1_c 1_t})$$

Erstellen einer neuen Q#-Datei

Öffnen Sie Visual Studio Code.
Wählen Sie Datei > Neue Textdatei aus, und speichern Sie diese als Main.qs.
Wählen Sie Ansicht -> Befehlspalette und Typ Q# aus: Legen Sie das Azure Quantum QIRtarget Profil fest. Drücken Sie die EINGABETASTE.
Wählen Sie Q#: Nicht eingeschränkt.

Erstellen des Bell-Zustands $\ket{\phi^+}$

Beginnen wir mit dem Erstellen des Bell-Zustands $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.

Zunächst müssen Sie den Microsoft.Quantum.Diagnostics-Namespace aus der Standardbibliothek importieren, die die DumpMachine-Funktion enthält. Diese Funktion zeigt den aktuellen Zustand des Qubits an. Kopieren Sie den folgenden Q#-Code, und fügen Sie ihn in die Datei Main.qs ein.
```
import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
```
Tipp

Sie können die Standardbibliothek auch importieren, indem Sie Microsoft.Quantum durch Std ersetzen. import Std.Diagnostics.* entspricht beispielsweise import Microsoft.Quantum.Diagnostics.*.

Erstellen Sie den Main-Vorgang, der zwei Result-Typwerte zurückgibt, bei denen es sich um die Messergebnisse der Qubits handelt.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    // Your code goes here
}

Innerhalb des Main-Vorgangs weisen Sie zwei Qubits, q1 und q2 zu, die verschränkt werden.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());
}

Wenden Sie das Hadamard-Gate, H, auf das erste Qubit, q1, an, um es in einen Superpositionszustand zu versetzen. Verschränken Sie dann die beiden Qubits mithilfe des CNOT-Vorgangs.
```
import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
}
```

Verwenden Sie die DumpMachine-Funktion, um den aktuellen Status der Qubits anzuzeigen. Dies ist nicht identisch mit der Messung der Qubits.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();
}

Messen Sie die Qubits mithilfe des M-Vorgangs, und speichern Sie die Ergebnisse in m1 und m2. Verwenden Sie dann den Reset-Vorgang, um die Qubits zurückzusetzen. In Q# müssen Sie die Qubits immer auf den Zustand $|0\rangle$ zurücksetzen.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {

    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

}

Geben Sie schließlich die Messergebnisse der Qubits mit der return-Anweisung zurück. Ihre Datei Main.qs sollte wie folgt aussehen:

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

Um Ihr Programm auf dem integrierten Simulator auszuführen, klicken Sie über dem Vorgang Main auf Ausführen, oder drücken Sie STRG+F5. Die Ausgabe wird in der Debugkonsole angezeigt.
Die Messergebnisse werden korreliert, sodass Sie am Ende des Programms ein Ergebnis von (Zero, Zero) oder (One, One) mit gleicher Wahrscheinlichkeit erhalten.
Sie können das Schaltungsdiagramm visualisieren, indem Sie auf Schaltung in der Liste der Befehle über dem Main-Vorgang klicken. Das Schaltungsdiagramm zeigt das Hadamard-Gate, das auf das erste Qubit angewendet wird, und das CNOT-Gate, das auf beide Qubits angewendet wird.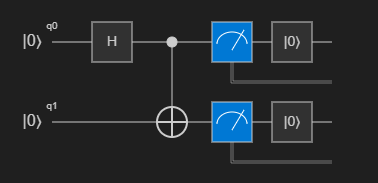

Erstellen anderer Bell-Zustände

Um weitere Bell-Zustände zu erstellen, müssen Sie zusätzliche Pauli $X$- und $Z$-Vorgänge auf die Qubits anwenden.

Um z. B. den Bell-Zustand $\ket{\phi^-}=\frac1{\sqrt2}(|00-11\rangle|\rangle)$ zu erstellen, können Sie den Pauli $Z-Vorgang$ auf das Steuerungsqubit anwenden, nachdem das Hadamard-Gate angewendet wurde. Der $Z-Vorgang$ schaltet den Zustand $\ket{+}$ in $\ket{-}$ um.

Tipp

Die Zustände $\frac{{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ und $\frac{1}{\sqrt{{2}}(|0\rangle -|1\rangle)$ werden auch als $\ket{+}$ bzw $\ket{{-}$ bezeichnet.

So funktioniert es:

Nehmen Sie zum Beispiel zwei Qubits mit dem Zustand $|00\rangle$.
Erstellen Sie durch Anwenden von $$H$ ein Superpositionszustand nur im Steuerungsqubit vor.

$$H |0_c\rangle=\frac{{1}{\sqrt{2}}(|0_c\rangle+|1_c\rangle) =\ket{+}_c$$
Wenden Sie den $Z-Vorgang$ auf das Steuerungsqubit an.

$$Z \frac{{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)=\frac{1}{\sqrt{{2}}(|0_c\rangle-|1_c\rangle)=\ket{{-}_c$$
Wenden Sie den $CNOT-Operator$ auf das Steuerungsqubit und den target Qubit an, der sich im Zustand $|0_t\rangle$ befindet.

$$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c}-\ket{1_c})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}-|\ket{1_c 0_t})=$$$$=\frac{{1}{\sqrt2}(CNOT \ket{0_c 0_t} - CNOT \ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t}-\ket{1_c 1_t})$$

Ebenso können Bell-Zustände $\ket{\psi^+}$ und $\ket{\psi^-}$ erstellt werden, indem die Pauli $X$- und $Z-Vorgänge$ auf die Qubits angewendet werden.

Der Bell-Zustand $\ket{\psi^+}=\frac1{\sqrt2}(|01\rangle+|10\rangle)$ kann erstellt werden, indem der Pauli $X-Vorgang$ auf das target Qubit angewendet wird, nachdem das Hadamard-Gate angewendet wurde.
Der Bell-Zustand $\ket{\psi^-}=\frac1{\sqrt2}(|01-10\rangle\rangle|)$ kann erstellt werden, indem das Pauli $Z$ auf das Steuerungsqubit und das Pauli $X$ auf den target Qubit angewendet werden, nachdem das Hadamard-Gate angewendet wurde.

Erstellen des Bell-Zustands $\ket{\phi^-}$ in Q#

Ändern Sie den Q# Code, um den Bell-Zustand $\ket{\phi^-}$ zu erstellen. Ihre Datei Main.qs sollte wie folgt aussehen:

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    Z(q1); // Apply the Pauli Z operation to the control qubit
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

Um Ihr Programm auf dem integrierten Simulator auszuführen, klicken Sie über dem Vorgang Main auf Ausführen, oder drücken Sie STRG+F5. Die Ausgabe wird in der Debugkonsole angezeigt.
Sie können das Schaltungsdiagramm visualisieren, indem Sie auf Schaltung in der Liste der Befehle über dem Main-Vorgang klicken. Das Schaltungsdiagramm zeigt das Hadamard-Gate, das auf das erste Qubit angewendet wird, das Pauli $Z$-Gate, das auf das erste Qubit angewendet wird, und das CNOT-Gate, das auf beide Qubits angewendet wird.

In der nächsten Einheit erfahren Sie, wie Sie die Quantenverschränkung verwenden, um Quanteninformationen zu teleportieren.