Was ist Verschränkung?

  • 5 Minuten

Die Verschränkung ist eines der wichtigsten Merkmale der Quantenmechanik, die sie von der klassischen Mechanik unterscheidet. Aber was ist nun eigentlich Verschränkung? Wie funktioniert dies? Und warum ist es für Quanteninformationen so wichtig?

In dieser Lektion erfahren Sie, wie Sie die Quantenverschränkung definieren und beschreiben, und verstehen, warum es eine so leistungsstarke Ressource für Quantencomputing ist.

Die Quantenverschränkung verstehen

Stellen Sie sich vor, Sie haben zwei Qubits, $A$ und $B$. Die Qubits sind voneinander unabhängig, was bedeutet, dass die Informationen über den Zustand von Qubit $A$, was auch immer er ist, nur zu Qubit $A$ gehört. Ebenso gehören die Informationen zum Zustand von Qubit $B$ zu Qubit $B$. Sie können den Zustand der einzelnen Qubits beschreiben. In diesem Fall sind die Qubits nicht verschränkt, da sie keine Informationen teilen.

Stellen Sie sich nun vor, dass Sie die Qubits verschränken (Sie erfahren später, wie Sie dies tun). Wenn Qubits $A$ und $B$ verschränkt sind, sind die Informationen über den Zustand von Qubit $A$ nicht unabhängig vom Zustand von Qubit $B$. Wenn sie verschränkt werden, werden Informationen zwischen beiden Qubits geteilt, und es gibt keine Möglichkeit, den Zustand von Qubit $A$ oder den Zustand von Qubit $B$ abzuleiten. Sie können nur den Zustand des globalen Systems beschreiben, nicht den Zustand der einzelnen Qubits.

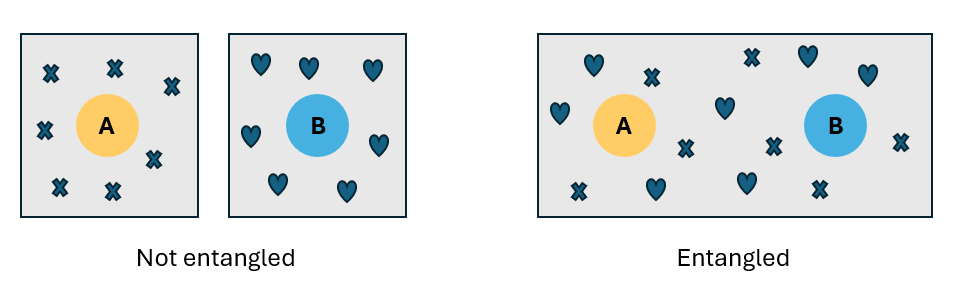
Diagramm mit zwei Qubits in zwei verschiedenen Situationen, nicht verschränkt und verschränkt. Wenn sie verschränkt werden, werden Informationen zwischen beiden Qubits geteilt, und es gibt keine Möglichkeit, Informationen abzuleiten, die nur Qubit A oder Qubit B gehören.

Die Verschränkung ist eine Quantenkorrelation zwischen zwei oder mehr Partikeln. Wenn zwei Partikel verschränkt sind, können sie nicht unabhängig, sondern nur als ganzes System beschrieben werden.

Beschreiben der Quantenverschränkung

Stellen Sie sich zwei Qubits $A$ und $B$ so vor, dass der Zustand des globalen Systems $\ket{\phi}$ folgender ist:

$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B})$$

Hinweis

In Dirac-Notation 0_A 0_B $\ket{}=|0_\text{A|}0\rangle\rangle_\text{B.}$ Die erste Position entspricht dem ersten Qubit und die zweite Position entspricht dem zweiten Qubit.

Das globale System $\ket{\phi}$ befindet sich in einer Superposition der Zustände $|00\rangle$ und $|11\rangle$. Wenn Sie beide Qubits messen, sind nur zwei Ergebnisse möglich: $\ket{{00}$ und $\ket{{11}$, und jedes hat die gleiche Wahrscheinlichkeit von $\frac{1}{{2}$.

Aber was ist der individuelle Zustand von Qubit $A$? Und von Qubit $B$? Wenn Sie versuchen, den Zustand von Qubit $A$ zu beschreiben, ohne den Zustand von Qubit $B$ zu berücksichtigen, würde dies fehlschlagen. Teilsysteme $A$ und $B$ sind verschränkt, was bedeutet, dass sie korreliert sind und nicht unabhängig voneinander beschrieben werden können.

Tipp

Wenn Sie mit Algebra und Dirac-Notation vertraut sind, besteht eine gute Übung darin, den $\ket{\phi}$ Zustand zu ändern, um etwas wie den Zustand von Qubit $A$ mal den Zustand von Qubit $B$ zu erhalten. Wenn Sie versuchen, die Klammer zu erweitern, den gemeinsamen Faktor zu erhalten usw., sehen Sie, dass es nicht möglich ist.

Der Quantenzustand $\ket{\phi}$ ist ein spezieller verschränkter Zustand, der als Bell-Zustand bezeichnet wird. Es gibt vier Bell-Zustände.

$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{{00} + \frac1{\sqrt2}\ket{{11}$$$$\ket{\phi^{-}}=\frac1{\sqrt2}\ket{00} - \frac1{\sqrt2}\ket{11}$$$$\ket{\psi^{+}}=\frac1{\sqrt2}\ket{{01} + \frac1{\sqrt2}\ket{{10}$$$$\ket{\psi^{-}}=\frac1{\sqrt2}\ket{01} - \frac1{\sqrt2}\ket{10}$$

Verwenden von Verschränkung als Ressource

An diesem Punkt fragen Sie sich vielleicht, was ist das große Problem bei der Verschränkung?

Wenn zwei Partikel miteinander verbunden sind, werden Subsysteme korreliert und können nicht unabhängig voneinander beschrieben werden. Aber hier ist der interessante Teil: Die Messergebnisse sind ebenfalls korreliert. Das heißt, welcher Vorgang mit dem Zustand eines Qubits in einem verschränkten Paar geschieht, wirkt sich auch auf den Zustand des anderen Qubits aus.

Sehen Sie sich dies beispielsweise für den $\ket{\phi^{+}}$ Zustand an,

$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{{00} + \frac1{\sqrt2}\ket{{11}$$

Wenn Sie beide Qubits messen, erhalten Sie entweder $|00\rangle$ oder $|11\rangle$ mit gleicher Wahrscheinlichkeit. Es gibt keine Wahrscheinlichkeit, die Zustände $|01\rangle$ und $|10\rangle$ zu erhalten.

Aber was geschieht, wenn Sie nur ein Qubit messen?

Wenn Sie nur den Qubit $A$ messen und den Status $|0\rangle$ erhalten, bedeutet dies, dass das globale System in den Zustand $\ket{00}$reduziert wird. Dies ist das einzige mögliche Ergebnis, da die Wahrscheinlichkeit der Messung von $|01\rangle$ null ist.

Daher können Sie ohne Messung des Qubits $B$ sicher sein, dass sich der zweite Qubit auch im Zustand $|0\rangle$ befindet. Die Messergebnisse korrelieren, weil die Qubits verschränkt sind.

Verschränkung kann zwischen zwei Partikeln bestehen, auch wenn sie durch große Entfernungen voneinander getrennt sind. Diese Korrelation ist stärker als jede klassische Korrelation, und es ist eine wichtige Ressource für Quanteninformationsverarbeitungsaufgaben wie Quantenteleportation, Quantenkryptografie und Quantencomputing.