Drei Typen von Bézier-Kurven
Erfahren Sie, wie Sie mithilfe von SkiaSharp kubische, quadratische und konische Bézierkurven rendern.
Die Bézierkurve ist nach Pierre Bézier (1910 – 1999), einem französischen Ingenieur des Automobilunternehmens Renault benannt, der die Kurve für die computergestützte Konstruktion von Karosserien verwendet hat.
Bézierkurven sind bekannt dafür, dass sie gut für interaktives Design geeignet sind: Sie sind gut verhalten – mit anderen Worten, es gibt keine Singularitäten, die dazu führen, dass die Kurve unendlich oder unübersichtlich wird – und sie sind im Allgemeinen ästhetisch ansprechend:

Zeichengliederungen von computerbasierten Schriftarten werden in der Regel mit Bézierkurven definiert.
Der Wikipedia-Artikel zur Bézierkurve enthält einige nützliche Hintergrundinformationen. Der Begriff Bézierkurve bezieht sich tatsächlich auf eine Familie ähnlicher Kurven. SkiaSharp unterstützt drei Arten von Bézierkurven, die als Kubik, quadratisch und konisch bezeichnet werden. Der Kegel wird auch als rationales Quadrat bezeichnet.
Die kubische Bézierkurve
Die Kubik ist die Art der Bézierkurve, die die meisten Entwickler denken, wenn das Thema der Bézierkurven aufkommt.
Sie können einem SKPath Objekt eine kubische Bézierkurve hinzufügen, indem Sie die CubicTo Methode mit drei SKPoint Parametern oder die CubicTo Überladung mit separaten x Parametern und y Parametern verwenden:
public void CubicTo (SKPoint point1, SKPoint point2, SKPoint point3)
public void CubicTo (Single x1, Single y1, Single x2, Single y2, Single x3, Single y3)
Die Kurve beginnt am aktuellen Punkt der Kontur. Die vollständige kubische Bézierkurve wird durch vier Punkte definiert:
- Startpunkt: aktueller Punkt in der Kontur oder (0, 0) wenn
MoveTonicht aufgerufen wurde - erster Kontrollpunkt:
point1imCubicToAnruf - zweiter Kontrollpunkt:
point2imCubicToAnruf - Endpunkt:
point3imCubicToAnruf
Die resultierende Kurve beginnt am Anfangspunkt und endet am Endpunkt. Die Kurve verläuft in der Regel nicht durch die beiden Kontrollpunkte; Stattdessen funktionieren die Kontrollpunkte ähnlich wie Magnete, um die Kurve zu ihnen zu ziehen.
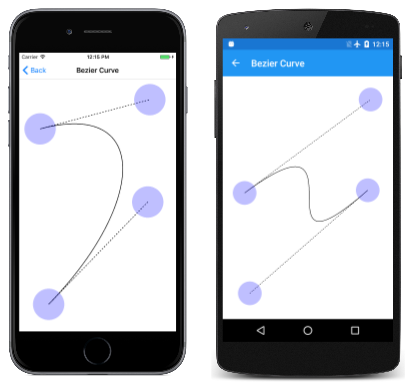
Die beste Möglichkeit, ein Gefühl für die kubische Bézierkurve zu bekommen, ist das Experimentieren. Dies ist der Zweck der Seite " Bézierkurve ", die von InteractivePage. Die Datei "BezierCurvePage.xaml" instanziiert die SKCanvasView und eine TouchEffect. Die BezierCurvePage.xaml.cs CodeBehind-Datei erstellt vier TouchPoint Objekte im Konstruktor. Der PaintSurface Ereignishandler erstellt eine SKPath Bézierkurve basierend auf den vier TouchPoint Objekten und zeichnet auch gepunktete Tangenslinien von den Kontrollpunkten bis zu den Endpunkten:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with cubic Bezier curve
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.CubicTo(touchPoints[1].Center,
touchPoints[2].Center,
touchPoints[3].Center);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[2].Center.X,
touchPoints[2].Center.Y,
touchPoints[3].Center.X,
touchPoints[3].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
Hier wird folgendes ausgeführt:
Mathematisch ist die Kurve ein kubisches Polynom. Die Kurve überschneidet eine gerade Linie höchstens an drei Punkten. Am Anfangspunkt ist die Kurve immer tangensiert und in derselben Richtung wie eine gerade Linie vom Startpunkt zum ersten Kontrollpunkt. Am Endpunkt ist die Kurve immer tangensiert und in derselben Richtung wie eine gerade Linie vom zweiten Kontrollpunkt zum Endpunkt.
Die kubische Bézierkurve wird immer durch eine konvexe Viereckkurve begrenzt, die die vier Punkte verbindet. Dies wird als konvexer Rumpf bezeichnet. Wenn sich die Kontrollpunkte auf der geraden Linie zwischen Start und Endpunkt befinden, wird die Bézierkurve als gerade Linie gerendert. Die Kurve kann sich aber auch selbst kreuzen, wie der dritte Screenshot zeigt.
Eine Pfadprofil kann mehrere verbundene kubische Bézierkurven enthalten, die Verbindung zwischen zwei kubischen Bézierkurven ist jedoch nur glatt, wenn die folgenden drei Punkte kolinear sind (d. r. auf einer geraden Linie):
- der zweite Kontrollpunkt der ersten Kurve
- der Endpunkt der ersten Kurve, die auch der Startpunkt der zweiten Kurve ist
- der erste Kontrollpunkt der zweiten Kurve
Im nächsten Artikel zu SVG-Pfaddaten entdecken Sie eine Einrichtung, um die Definition reibungslos verbundener Bézierkurven zu vereinfachen.
Es ist manchmal nützlich, die zugrunde liegenden parametrischen Formeln zu kennen, die eine kubische Bézierkurve rendern. Für t von 0 bis 1 sind die parametrischen Gleichungen wie folgt:
x(t) = (1 – t)¹x₀ + 3t(1 – t)²x₁ + 3t²(1 – t)x₃
y(t) = (1 – t)¹y₀ + 3t(1 – t)²y₁ + 3t²(1 – t)y₃
Der höchste Exponent von 3 bestätigt, dass es sich um kubische Polynome handelt. Es ist leicht zu überprüfen, ob der t Punkt gleich 0 ist (x₀, y₀), was der Anfangspunkt ist und wenn t gleich 1, der Punkt ist (x₃, y₃), was der Endpunkt ist. Der erste Kontrollpunkt (x₁, y₁) hat in der Nähe des Startpunkts (für niedrige Werte tvon 't') einen starken Effekt, und in der Nähe des Endpunkts (hohe Werte von 't') hat der zweite Kontrollpunkt (x₁, y₁) eine starke Wirkung.
Bézierkurve Näherung an Kreisbögen
Es ist manchmal praktisch, eine Bézierkurve zu verwenden, um einen kreisförmigen Bogen zu rendern. Eine kubische Bézierkurve kann einen kreisförmigen Bogen sehr gut bis zu einem Viertelkreis annähern, sodass vier verbundene Bézierkurven einen ganzen Kreis definieren können. Diese Annäherung wird vor über 25 Jahren in zwei Artikeln diskutiert:
Tor Dokken, et al, "Good Approximation of Circles by Curvature-Continuous Bézier curves", Computer Aided Geometric Design 7 (1990), 33-41.
Michael Goldapp, "Näherung der Kreisbögen durch kubische Polynomen", Computer aided Geometric Design 8 (1991), 227-238.
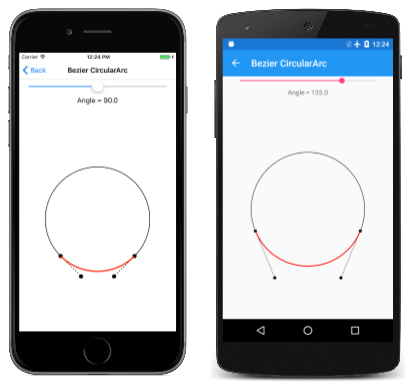
Das folgende Diagramm zeigt vier Punkte mit beschrifteten pto, pt1, pt2, und pt3 definieren eine Bézierkurve (in Rot dargestellt), die einen kreisförmigen Bogen annähert:
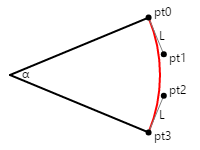
Die Linien von Start- und Endpunkten bis zu den Kontrollpunkten sind tangens zum Kreis und zur Bézierkurve, und sie haben eine Länge von L. Der erste oben genannte Artikel weist darauf hin, dass die Bézierkurve einen kreisförmigen Bogen am besten annähert, wenn diese Länge L wie folgt berechnet wird:
L = 4 × Tan(α / 4) / 3
Die Abbildung zeigt einen Winkel von 45 Grad, sodass L gleich 0,265 ist. Im Code würde dieser Wert mit dem gewünschten Radius des Kreises multipliziert.
Auf der Seite " Bézier Kreisbogen " können Sie mit der Definition einer Bézierkurve experimentieren, um einen kreisförmigen Bogen für Winkel von bis zu 180 Grad anzunähern. Die Datei "BezierCircularArcPage.xaml" instanziiert den SKCanvasView Winkel und eine Slider zum Auswählen des Winkels. Der PaintSurface Ereignishandler in der BezierCircularArgPage.xaml.cs CodeBehind-Datei verwendet eine Transformation, um den Punkt (0, 0) auf die Mitte des Zeichenbereichs festzulegen. Er zeichnet einen Kreis, der für den Vergleichspunkt zentriert ist, und berechnet dann die beiden Kontrollpunkte für die Bézierkurve:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Translate to center
canvas.Translate(info.Width / 2, info.Height / 2);
// Draw the circle
float radius = Math.Min(info.Width, info.Height) / 3;
canvas.DrawCircle(0, 0, radius, blackStroke);
// Get the value of the Slider
float angle = (float)angleSlider.Value;
// Calculate length of control point line
float length = radius * 4 * (float)Math.Tan(Math.PI * angle / 180 / 4) / 3;
// Calculate sin and cosine for half that angle
float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);
// Find the end points
SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
SKPoint point3 = new SKPoint(radius * sin, radius * cos);
// Find the control points
SKPoint point0Normalized = Normalize(point0);
SKPoint point1 = point0 + new SKPoint(length * point0Normalized.Y,
-length * point0Normalized.X);
SKPoint point3Normalized = Normalize(point3);
SKPoint point2 = point3 + new SKPoint(-length * point3Normalized.Y,
length * point3Normalized.X);
// Draw the points
canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);
canvas.DrawCircle(point3.X, point3.Y, 10, blackFill);
// Draw the tangent lines
canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
canvas.DrawLine(point3.X, point3.Y, point2.X, point2.Y, dottedStroke);
// Draw the Bezier curve
using (SKPath path = new SKPath())
{
path.MoveTo(point0);
path.CubicTo(point1, point2, point3);
canvas.DrawPath(path, redStroke);
}
}
// Vector methods
SKPoint Normalize(SKPoint v)
{
float magnitude = Magnitude(v);
return new SKPoint(v.X / magnitude, v.Y / magnitude);
}
float Magnitude(SKPoint v)
{
return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
}
Die Anfangs- und Endpunkte (point0 und point3) werden basierend auf den normalen parametrischen Formeln für den Kreis berechnet. Da der Kreis zentriert ist (0, 0), können diese Punkte auch als Radialvektoren aus der Mitte des Kreises bis zum Umfang behandelt werden. Die Kontrollpunkte befinden sich in Linien, die tangens zum Kreis sind, sodass sie sich in rechten Winkeln zu diesen Radialvektoren befinden. Ein Vektor in einem rechten Winkel zu einem anderen ist einfach der ursprüngliche Vektor mit den getauschten X- und Y-Koordinaten und einer davon negativ.
Hier ist das Programm, das mit verschiedenen Winkeln ausgeführt wird:
Sehen Sie sich den dritten Screenshot genau an, und Sie werden sehen, dass die Bézier-Kurve vor allem von einem Halbkreis abweicht, wenn der Winkel 180 Grad beträgt, aber der iOS-Bildschirm zeigt, dass es scheinbar einen Viertelkreis passt, genau richtig, wenn der Winkel 90 Grad beträgt.
Die Berechnung der Koordinaten der beiden Kontrollpunkte ist recht einfach, wenn der Viertelkreis wie folgt ausgerichtet ist:
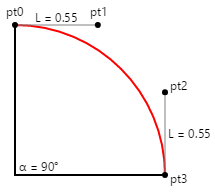
Wenn der Radius des Kreises 100 ist, dann ist L 55, und das ist eine einfache Zahl.
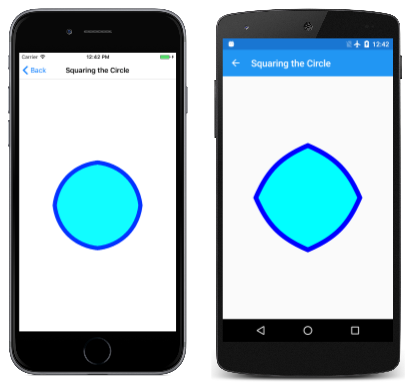
Das Quadrat auf der Kreisseite animiert eine Figur zwischen einem Kreis und einem Quadrat. Der Kreis wird mit vier Bézierkurven angenähert, deren Koordinaten in der ersten Spalte dieser Arraydefinition in der SquaringTheCirclePage Klasse angezeigt werden:
public class SquaringTheCirclePage : ContentPage
{
SKPoint[,] points =
{
{ new SKPoint( 0, 100), new SKPoint( 0, 125), new SKPoint() },
{ new SKPoint( 55, 100), new SKPoint( 62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 100, 55), new SKPoint( 62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 100, 0), new SKPoint( 125, 0), new SKPoint() },
{ new SKPoint( 100, -55), new SKPoint( 62.5f, -62.5f), new SKPoint() },
{ new SKPoint( 55, -100), new SKPoint( 62.5f, -62.5f), new SKPoint() },
{ new SKPoint( 0, -100), new SKPoint( 0, -125), new SKPoint() },
{ new SKPoint( -55, -100), new SKPoint(-62.5f, -62.5f), new SKPoint() },
{ new SKPoint(-100, -55), new SKPoint(-62.5f, -62.5f), new SKPoint() },
{ new SKPoint(-100, 0), new SKPoint( -125, 0), new SKPoint() },
{ new SKPoint(-100, 55), new SKPoint(-62.5f, 62.5f), new SKPoint() },
{ new SKPoint( -55, 100), new SKPoint(-62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 0, 100), new SKPoint( 0, 125), new SKPoint() }
};
...
}
Die zweite Spalte enthält die Koordinaten von vier Bézierkurven, die ein Quadrat definieren, dessen Fläche ungefähr dem Bereich des Kreises entspricht. (Das Zeichnen eines Quadrats mit dem genauen Bereich als gegebener Kreis ist das klassische, unlösbare geometrische Problem beim Quadratieren des Kreises.) Zum Rendern eines Quadrats mit Bézierkurven sind die beiden Kontrollpunkte für jede Kurve identisch, und sie sind mit den Anfangs- und Endpunkten kolinear, sodass die Bézierkurve als gerade Linie gerendert wird.
Die dritte Spalte des Arrays ist für interpolierte Werte für eine Animation. Die Seite legt einen Timer für 16 Millisekunden fest, und der PaintSurface Handler wird mit dieser Rate aufgerufen:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(Math.Min(info.Width / 300, info.Height / 300));
// Interpolate
TimeSpan timeSpan = new TimeSpan(DateTime.Now.Ticks);
float t = (float)(timeSpan.TotalSeconds % 3 / 3); // 0 to 1 every 3 seconds
t = (1 + (float)Math.Sin(2 * Math.PI * t)) / 2; // 0 to 1 to 0 sinusoidally
for (int i = 0; i < 13; i++)
{
points[i, 2] = new SKPoint(
(1 - t) * points[i, 0].X + t * points[i, 1].X,
(1 - t) * points[i, 0].Y + t * points[i, 1].Y);
}
// Create the path and draw it
using (SKPath path = new SKPath())
{
path.MoveTo(points[0, 2]);
for (int i = 1; i < 13; i += 3)
{
path.CubicTo(points[i, 2], points[i + 1, 2], points[i + 2, 2]);
}
path.Close();
canvas.DrawPath(path, cyanFill);
canvas.DrawPath(path, blueStroke);
}
}
Die Punkte werden basierend auf einem sinusförmigen oszillierenden Wert von tinterpoliert. Die interpolierten Punkte werden dann verwendet, um eine Reihe von vier verbundenen Bézierkurven zu konstruieren. Die folgende Animation wird ausgeführt:
Eine solche Animation wäre ohne Kurven unmöglich, die algorithmisch flexibel genug sind, um als kreisförmige Bögen und gerade Linien gerendert zu werden.
Die Seite "Bezier Infinity " nutzt auch die Fähigkeit einer Bézierkurve, einen kreisförmigen Bogen anzunähern. Dies ist der PaintSurface Handler aus der BezierInfinityPage Klasse:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPath path = new SKPath())
{
path.MoveTo(0, 0); // Center
path.CubicTo( 50, -50, 95, -100, 150, -100); // To top of right loop
path.CubicTo( 205, -100, 250, -55, 250, 0); // To far right of right loop
path.CubicTo( 250, 55, 205, 100, 150, 100); // To bottom of right loop
path.CubicTo( 95, 100, 50, 50, 0, 0); // Back to center
path.CubicTo( -50, -50, -95, -100, -150, -100); // To top of left loop
path.CubicTo(-205, -100, -250, -55, -250, 0); // To far left of left loop
path.CubicTo(-250, 55, -205, 100, -150, 100); // To bottom of left loop
path.CubicTo( -95, 100, -50, 50, 0, 0); // Back to center
path.Close();
SKRect pathBounds = path.Bounds;
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(0.9f * Math.Min(info.Width / pathBounds.Width,
info.Height / pathBounds.Height));
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Blue;
paint.StrokeWidth = 5;
canvas.DrawPath(path, paint);
}
}
}
Es kann eine gute Übung sein, diese Koordinaten auf Diagrammpapier zu zeichnen, um zu sehen, wie sie miteinander verbunden sind. Das Unendlichkeitszeichen wird um den Punkt (0, 0) zentriert, und die beiden Schleifen haben Mittelpunkte von (–150, 0) und (150, 0) und Radien von 100. In der Reihe von CubicTo Befehlen können Sie X-Koordinaten von Kontrollpunkten sehen, die werte von –95 und –205 (diese Werte sind –150 plus und minus 55), 205 und 95 (150 plus und minus 55) sowie 250 und -250 für die rechte und linke Seite. Die einzige Ausnahme ist, wenn sich das Unendlichkeitszeichen in der Mitte kreuzt. In diesem Fall weisen Kontrollpunkte Koordinaten mit einer Kombination von 50 und –50 auf, um die Kurve in der Nähe der Mitte zu begradigen.
Hier ist das Unendlichkeitszeichen:
Es ist etwas glatter in Richtung der Mitte als das Unendlichkeitszeichen, das von der Arc Infinity-Seite aus dem Artikel "Three Ways to Draw an Arc" gerendert wird.
Die quadratische Bézierkurve
Die quadratische Bézierkurve weist nur einen Kontrollpunkt auf, und die Kurve wird durch nur drei Punkte definiert: der Startpunkt, der Kontrollpunkt und der Endpunkt. Die parametrischen Gleichungen sind der kubischen Bézierkurve sehr ähnlich, mit der Ausnahme, dass der höchste Exponent 2 ist, sodass die Kurve ein quadratisches Polynom ist:
x(t) = (1 – t)²x₀ + 2t(1 – t)x₁ + t²x²
y(t) = (1 – t)²y₀ + 2t(1 – t)y₁ + t²y₁
Zum Hinzufügen einer quadratischen Bézierkurve zu einem Pfad verwenden Sie die QuadTo Methode oder die QuadTo Überladung mit separaten x Koordinaten und y Koordinaten:
public void QuadTo (SKPoint point1, SKPoint point2)
public void QuadTo (Single x1, Single y1, Single x2, Single y2)
Mit den Methoden wird eine Kurve von der aktuellen Position als point2point1 Kontrollpunkt hinzugefügt.
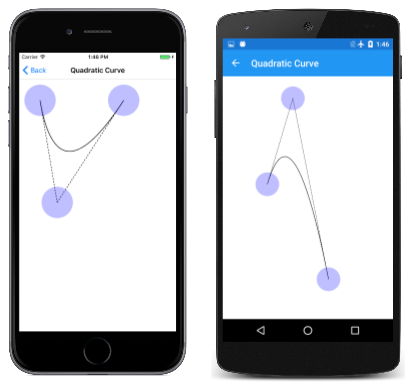
Sie können mit quadratischen Bézierkurven mit der Seite "Quadratische Kurve " experimentieren, die der Seite " Bézierkurve " sehr ähnlich ist, mit der Ausnahme, dass nur drei Berührungspunkte vorhanden sind. Dies ist der PaintSurface Handler in der QuadraticCurve.xaml.cs CodeBehind-Datei:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with quadratic Bezier
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.QuadTo(touchPoints[1].Center,
touchPoints[2].Center);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[1].Center.X,
touchPoints[1].Center.Y,
touchPoints[2].Center.X,
touchPoints[2].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
Und hier wird folgendes ausgeführt:
Die gepunkteten Linien sind tangensiert zur Kurve am Anfangspunkt und Endpunkt und treffen sich am Kontrollpunkt.
Das quadratische Bézier ist gut, wenn Sie eine Kurve einer allgemeinen Form benötigen, aber Sie bevorzugen den Komfort nur eines Kontrollpunkts anstelle von zwei. Die quadratische Bézier rendert effizienter als jede andere Kurve, weshalb sie intern in Skia verwendet wird, um elliptische Bögen zu rendern.
Die Form einer quadratischen Bézierkurve ist jedoch nicht elliptisch, weshalb mehrere quadratische Béziers erforderlich sind, um einen elliptischen Bogen anzunähern. Das quadratische Bézier ist stattdessen ein Segment eines Parabola.
Die Kegelkurve
Die konische Bézierkurve , auch als rationale quadratische Bézierkurve bezeichnet, ist eine relativ jüngste Ergänzung zur Familie der Bézierkurven. Wie die quadratische Bézierkurve umfasst die rationale quadratische Bézierkurve einen Startpunkt, einen Endpunkt und einen Kontrollpunkt. Die rationale quadratische Bézierkurve erfordert jedoch auch einen Gewichtungswert . Es wird als rationales Quadrat bezeichnet, da die parametrischen Formeln Verhältnisse umfassen.
Die parametrischen Gleichungen für X und Y sind Verhältnisse, die denselben Nenner aufweisen. Dies ist die Gleichung für den Nenner für t von 0 bis 1 und ein Gewichtungswert von w:
d(t) = (1 – t)² + 2wt(1 – t) + t²
Theoretisch kann eine rationale Quadratik drei separate Gewichtungswerte umfassen, eine für jeden der drei Begriffe, aber diese können auf nur einen Gewichtungswert im mittleren Begriff vereinfacht werden.
Die parametrischen Formeln für die X- und Y-Koordinaten ähneln den parametrischen Formeln für die quadratische Bézier, mit der Ausnahme, dass der Mittelbegriff auch den Gewichtungswert enthält, und der Ausdruck wird durch den Nenner dividiert:
x(t) = ((1 – t)²x₀ + 2wt(1 – t)x₁ + t²xwei)) ÷ d(t)
y(t) = ((1 – t)²y₀ + 2wt(1 – t)y₁ + t²ywei)) ÷ d(t)
Rationale quadratische Bézierkurven werden auch als Konik bezeichnet, da sie genau Segmente eines konischen Abschnitts darstellen können – Hyperbolas, Parabolien, Ellipsen und Kreise.
Zum Hinzufügen einer rationalen quadratischen Bézierkurve zu einem Pfad verwenden Sie die ConicTo Methode oder die ConicTo Überladung mit separaten x Koordinaten und y Koordinaten:
public void ConicTo (SKPoint point1, SKPoint point2, Single weight)
public void ConicTo (Single x1, Single y1, Single x2, Single y2, Single weight)
Beachten Sie den endgültigen weight Parameter.
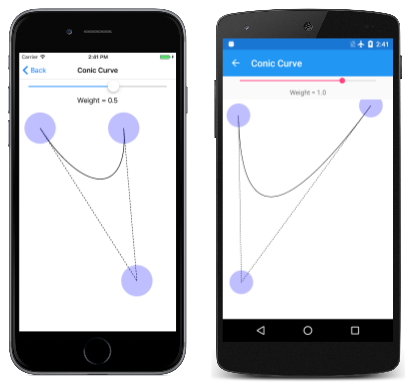
Auf der Seite "Kegelkurve " können Sie mit diesen Kurven experimentieren. Die ConicCurvePage-Klasse wird von InteractivePage abgeleitet. Die Datei ConicCurvePage.xaml instanziiert einen Slider Gewichtungswert zwischen -2 und 2. Die ConicCurvePage.xaml.cs CodeBehind-Datei erstellt drei TouchPoint Objekte, und der PaintSurface Handler rendert einfach die resultierende Kurve mit den Tangentenlinien an den Kontrollpunkten:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with conic curve
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.ConicTo(touchPoints[1].Center,
touchPoints[2].Center,
(float)weightSlider.Value);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[1].Center.X,
touchPoints[1].Center.Y,
touchPoints[2].Center.X,
touchPoints[2].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
Hier wird folgendes ausgeführt:
Wie Sie sehen können, scheint der Kontrollpunkt die Kurve mehr zu ziehen, wenn das Gewicht höher ist. Wenn die Gewichtung null ist, wird die Kurve zu einer geraden Linie vom Anfangspunkt zum Endpunkt.
Theoretisch sind negative Gewichte zulässig und führen dazu, dass sich die Kurve vom Kontrollpunkt abbiegen kann. Gewichtungen von -1 oder darunter führen jedoch dazu, dass der Nenner in den parametrischen Gleichungen für bestimmte Werte von t negativ wird. Aus diesem Grund werden negative Gewichtungen in den ConicTo Methoden ignoriert. Mit dem Conic Curve-Programm können Sie negative Gewichte festlegen, aber wie Sie sehen können, haben negative Gewichtungen den gleichen Effekt wie eine Gewichtung von Null und bewirken, dass eine gerade Linie gerendert wird.
Es ist sehr einfach, den Kontrollpunkt und die Gewichtung abzuleiten, um die ConicTo Methode zum Zeichnen eines Kreisbogens bis hin zu (aber nicht einschließlich) eines Halbkreiss zu verwenden. Im folgenden Diagramm treffen sich Tangenslinien von Anfang und Endpunkt am Kontrollpunkt.
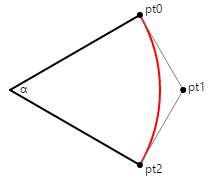
Sie können Trigonometrie verwenden, um den Abstand des Kontrollpunkts von der Mitte des Kreises zu bestimmen: Es ist der Radius des Kreises dividiert durch den Kosinus der Hälfte des Winkels α. Um einen kreisförmigen Bogen zwischen den Anfangs- und Endpunkten zu zeichnen, legen Sie die Gewichtung auf den gleichen Kosinus der Hälfte des Winkels fest. Beachten Sie, dass, wenn der Winkel 180 Grad beträgt, die Tangentenlinien niemals treffen und die Gewichtung null ist. Aber für Winkel unter 180 Grad funktioniert die Mathematik gut.
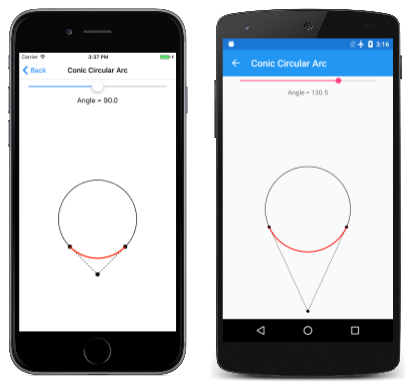
Auf der Seite Konic Circular Arc wird dies veranschaulicht. Die Datei ConicCircularArc.xaml instanziiert eine Slider zum Auswählen des Winkels. Der PaintSurface Handler in der ConicCircularArc.xaml.cs CodeBehind-Datei berechnet den Kontrollpunkt und die Gewichtung:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Translate to center
canvas.Translate(info.Width / 2, info.Height / 2);
// Draw the circle
float radius = Math.Min(info.Width, info.Height) / 4;
canvas.DrawCircle(0, 0, radius, blackStroke);
// Get the value of the Slider
float angle = (float)angleSlider.Value;
// Calculate sin and cosine for half that angle
float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);
// Find the points and weight
SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
SKPoint point1 = new SKPoint(0, radius / cos);
SKPoint point2 = new SKPoint(radius * sin, radius * cos);
float weight = cos;
// Draw the points
canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);
// Draw the tangent lines
canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
canvas.DrawLine(point2.X, point2.Y, point1.X, point1.Y, dottedStroke);
// Draw the conic
using (SKPath path = new SKPath())
{
path.MoveTo(point0);
path.ConicTo(point1, point2, weight);
canvas.DrawPath(path, redStroke);
}
}
Wie Sie sehen können, gibt es keinen visuellen Unterschied zwischen dem ConicTo in Rot angezeigten Pfad und dem zugrunde liegenden Kreis, der als Referenz angezeigt wird:
Legen Sie den Winkel jedoch auf 180 Grad fest, und die Mathematik schlägt fehl.
In diesem Fall ist es bedauerlich, dass ConicTo negative Gewichtungen nicht unterstützt werden, da der Kreis theoretisch (basierend auf den parametrischen Gleichungen) mit einem anderen Aufruf ConicTo mit denselben Punkten, aber einem negativen Wert der Gewichtung abgeschlossen werden kann. Dies würde das Erstellen eines ganzen Kreises mit nur zwei ConicTo Kurven basierend auf einem beliebigen Winkel zwischen (aber nicht einschließlich) Nullgrad und 180 Grad ermöglichen.