series_fit_poly()

Artikel
11/23/2024

Gilt für: ✅Microsoft Fabric ✅Azure Data Explorer✅Azure Monitor ✅Microsoft Sentinel

Wendet eine polynomiale Regression aus einer unabhängigen Variablen (x_series) auf eine abhängige Variable (y_series) an. Diese Funktion verwendet eine Tabelle mit mehreren Datenreihen (dynamische numerische Arrays) und generiert das am besten geeignete Polynom für jede Datenreihe mit polynomischer Regression.

Tipp

Verwenden Sie für die lineare Regression einer gleichmäßigen Datenreihe, wie sie vom Make-Series-Operator erstellt wurde, die einfachere Funktion series_fit_line(). Siehe Beispiel 2.
Wenn x_series angegeben wird und die Regression für einen hohen Grad durchgeführt wird, sollten Sie die Normalisierung auf den Bereich [0-1] in Betracht ziehen. Siehe Beispiel 3.
Wenn x_series vom Typ "datetime" ist, muss sie in "double" und "normalisiert" konvertiert werden. Siehe Beispiel 3.
Referenzimplementierung der polynomischen Regression mithilfe von Inline Python finden Sie unter series_fit_poly_fl().

Syntax

T | extend series_fit_poly( y_series [ , x_series , Grad ])

Erfahren Sie mehr über Syntaxkonventionen.

Parameter

Name	Type	Erforderlich	Beschreibung
y_series	`dynamic`	✔️	Ein Array numerischer Werte, die die abhängige Variable enthalten.
x_series	`dynamic`		Ein Array numerischer Werte, die die unabhängige Variable enthalten. Nur für ungleichmäßig angeordnete Reihen erforderlich. Wenn nicht angegeben, wird er auf einen Standardwert von [1, 2, ..., length(y_series)] festgelegt.
Grad			Die erforderliche Reihenfolge des Polynoms passt. Beispiel: 1 für lineare Regression, 2 für quadratische Regression usw. Der Standardwert ist 1, der die lineare Regression angibt.

Gibt zurück

Die series_fit_poly() Funktion gibt die folgenden Spalten zurück:

rsquare: r-square ist ein Standardmaß der Passqualität. Der Wert ist eine Zahl im Bereich [0-1], wobei 1 - die bestmögliche Übereinstimmung ist, und 0 bedeutet, dass die Daten ungeordnet sind und keine Zeile passen.
coefficients: Numerische Matrix mit den Koeffizienten des am besten angebrachten Polynoms mit dem angegebenen Grad, sortiert vom höchsten Potenzkoeffizienten bis zum niedrigsten.
variance: Varianz der abhängigen Variablen (y_series).
rvariance: Restabweichung, die die Varianz zwischen den Eingabedatenwerten ist, die angenähert sind.
poly_fit: Numerische Matrix mit einer Reihe von Werten des am besten geeigneten Polynoms. Die Länge der Datenreihe entspricht der Länge der abhängigen Variablen (y_series). Der Wert, der für die Diagrammerstellung verwendet wird.

Beispiele

Beispiel 1

Ein fünfter Ordnungsponom mit Rauschen auf x & y Achsen:

Abfrage ausführen

range x from 1 to 200 step 1
| project x = rand()*5 - 2.3
| extend y = pow(x, 5)-8*pow(x, 3)+10*x+6
| extend y = y + (rand() - 0.5)*0.5*y
| summarize x=make_list(x), y=make_list(y)
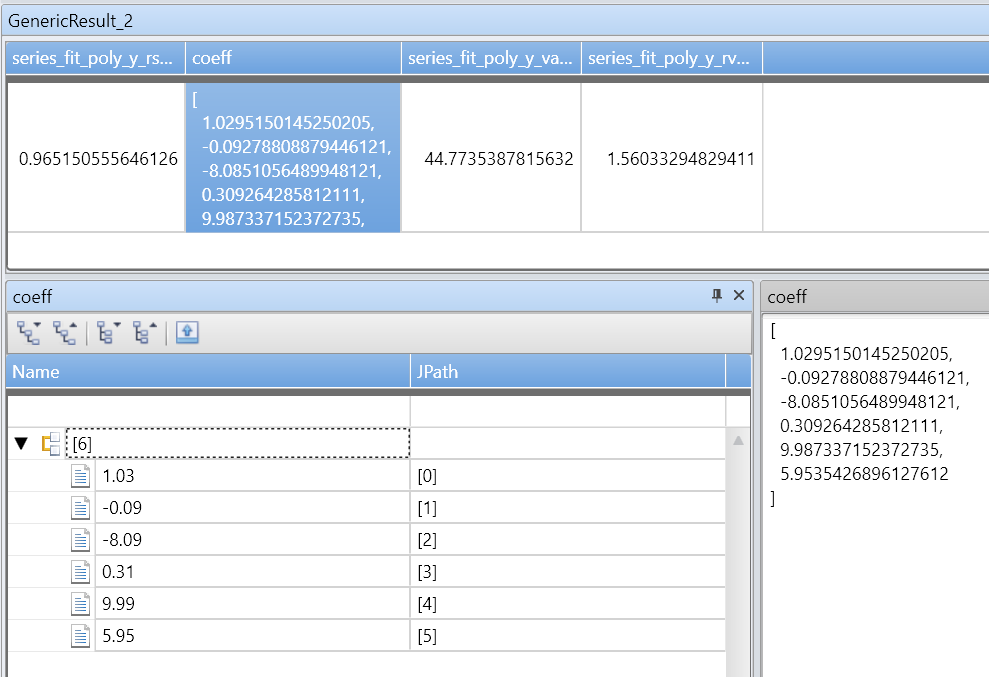
| extend series_fit_poly(y, x, 5)
| project-rename fy=series_fit_poly_y_poly_fit, coeff=series_fit_poly_y_coefficients
|fork (project x, y, fy) (project-away x, y, fy)
| render linechart

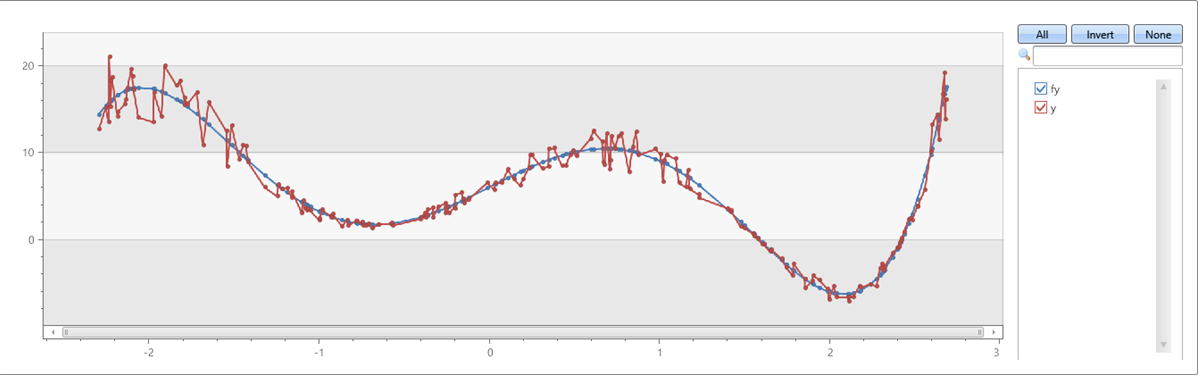
Diagramm mit fünfter Reihenfolge polynomischer Anpassung an eine Datenreihe mit Rauschen.

Koeffizienten der fünften Ordnung polynomisch passen zu einer Reihe mit Rauschen.

Beispiel 2

Überprüfen Sie, ob series_fit_poly mit Grad=1 übereinstimmungen series_fit_line:

demo_series1
| extend series_fit_line(y)
| extend series_fit_poly(y)
| project-rename y_line = series_fit_line_y_line_fit, y_poly = series_fit_poly_y_poly_fit
| fork (project x, y, y_line, y_poly) (project-away id, x, y, y_line, y_poly) 
| render linechart with(xcolumn=x, ycolumns=y, y_line, y_poly)

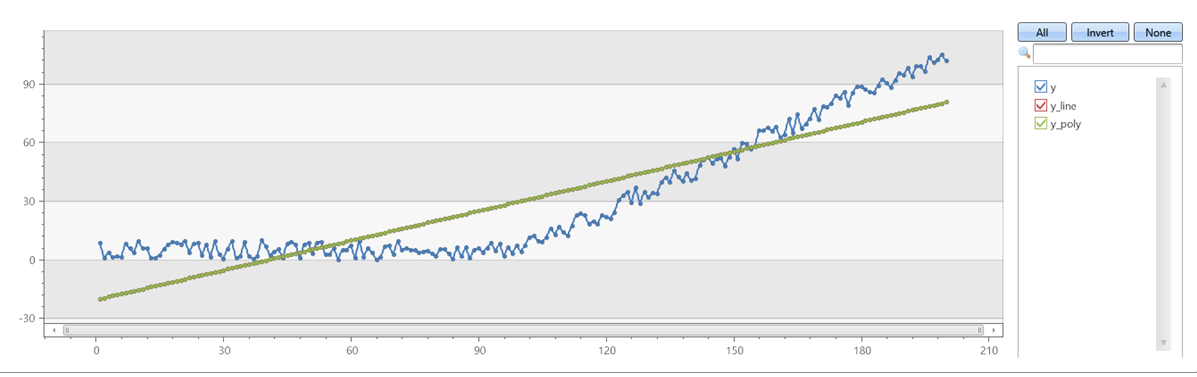
Diagramm mit linearer Regression.

Koeffizienten der linearen Regression.

Beispiel 3

Unregelmäßige Zeitreihen (ungleichmäßiger Abstand):

Abfrage ausführen

//
//  x-axis must be normalized to the range [0-1] if either degree is relatively big (>= 5) or original x range is big.
//  so if x is a time axis it must be normalized as conversion of timestamp to long generate huge numbers (number of 100 nano-sec ticks from 1/1/1970)
//
//  Normalization: x_norm = (x - min(x))/(max(x) - min(x))
//
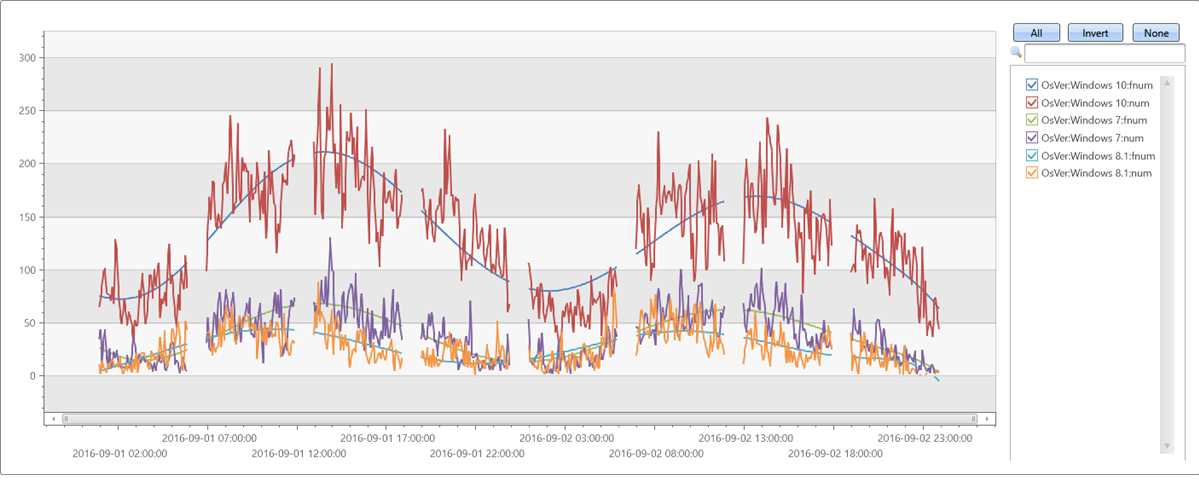
irregular_ts
| extend series_stats(series_add(TimeStamp, 0))                                                                 //  extract min/max of time axis as doubles
| extend x = series_divide(series_subtract(TimeStamp, series_stats__min), series_stats__max-series_stats__min)  // normalize time axis to [0-1] range
| extend series_fit_poly(num, x, 8)
| project-rename fnum=series_fit_poly_num_poly_fit
| render timechart with(ycolumns=num, fnum)

Diagramm mit achter Ordnung polynomischer Anpassung an eine unregelmäßige Zeitreihe.

Freigeben über