Globale und lokale Transformationen
Eine globale Transformation ist eine Transformation, die für jedes Element gilt, das von einem bestimmten Graphics-Objekt gezeichnet wird. Im Gegensatz dazu ist eine lokale Transformation eine Transformation, die für ein bestimmtes Element gilt, das gezeichnet werden soll.
Globale Transformationen
Um eine globale Transformation zu erstellen, erstellen Sie ein Graphics-Objekt, und bearbeiten Sie dann seine Transform-Eigenschaft. Die Transform-Eigenschaft ist ein Matrix-Objekt, weshalb es eine beliebige Abfolge affiner Transformationen enthalten kann. Die in der Transform-Eigenschaft gespeicherte Transformation wird als globale Transformation („Welttransformation“) bezeichnet. Die Graphics-Klasse bietet mehrere Methoden zum Aufbau einer zusammengesetzten globalen Transformation: MultiplyTransform, RotateTransform, ScaleTransform und TranslateTransform. Im folgenden Beispiel wird eine Ellipse zweimal gezeichnet: einmal vor dem Erstellen einer globalen Transformation und einmal danach. Die Transformation skaliert zunächst um einen Faktor von 0,5 in der Y-Richtung, führt dann eine Translation um 50 Einheiten in X-Richtung aus, und dreht das Element anschließend um 30 Grad.
myGraphics.DrawEllipse(myPen, 0, 0, 100, 50);
myGraphics.ScaleTransform(1, 0.5f);
myGraphics.TranslateTransform(50, 0, MatrixOrder.Append);
myGraphics.RotateTransform(30, MatrixOrder.Append);
myGraphics.DrawEllipse(myPen, 0, 0, 100, 50);
myGraphics.DrawEllipse(myPen, 0, 0, 100, 50)
myGraphics.ScaleTransform(1, 0.5F)
myGraphics.TranslateTransform(50, 0, MatrixOrder.Append)
myGraphics.RotateTransform(30, MatrixOrder.Append)
myGraphics.DrawEllipse(myPen, 0, 0, 100, 50)
Die folgende Abbildung zeigt die Matrizen, die an der Transformation beteiligt sind.
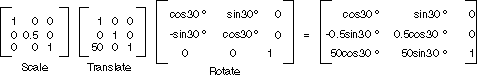
Hinweis
Im vorherigen Beispiel wird die Ellipse um den Ursprung des Koordinatensystems gedreht, der sich in der oberen linken Ecke des Clientbereichs befindet. Dies erzeugt ein anderes Ergebnis als die Drehung der Ellipse um ihr eigenes Zentrum.
Lokale Transformationen
Eine lokale Transformation gilt für ein bestimmtes Element, das gezeichnet werden soll. Beispielsweise verfügt ein GraphicsPath-Objekt über eine Transform-Methode, mit der Sie die Datenpunkte dieses Pfads transformieren können. Im folgenden Beispiel werden ein Rechteck ohne Transformation und ein Pfad mit einer Drehungstransformation gezeichnet. (Gehen Sie davon aus, dass es keine globale Transformation gibt.)
Matrix myMatrix = new Matrix();
myMatrix.Rotate(45);
myGraphicsPath.Transform(myMatrix);
myGraphics.DrawRectangle(myPen, 10, 10, 100, 50);
myGraphics.DrawPath(myPen, myGraphicsPath);
Dim myMatrix As New Matrix()
myMatrix.Rotate(45)
myGraphicsPath.Transform(myMatrix)
myGraphics.DrawRectangle(myPen, 10, 10, 100, 50)
myGraphics.DrawPath(myPen, myGraphicsPath)
Sie können die globale Transformation mit lokalen Transformationen kombinieren, um eine Vielzahl unterschiedlicher Ergebnisse zu erzielen. Sie können beispielsweise die globale Transformation verwenden, um das Koordinatensystem zu überarbeiten, und dann mit lokalen Transformationen Objekte drehen und skalieren, die in dem neuen Koordinatensystem gezeichnet werden.
Angenommen, Sie möchten ein Koordinatensystem erzeugen, dessen Ursprung 200 Pixel vom linken Rand des Clientbereichs und 150 Pixel vom oberen Rand des Clientbereichs entfernt liegt. Weiterhin angenommen, Sie möchten, dass die Maßeinheit Pixel sein soll, wobei die X-Achse nach rechts zeigt und die Y-Achse nach oben. Beim Standardkoordinatensystem zeigt die Y-Achse nach unten, weshalb Sie eine Spiegelung an der horizontalen Achse vornehmen müssen. Die folgende Abbildung zeigt die Matrix einer solchen Spiegelung.
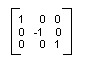
Angenommen, Sie müssen eine Translation von 200 Einheiten nach rechts und 150 Einheiten nach unten ausführen.
Im folgenden Beispiel wird das gerade beschriebene Koordinatensystem erstellt, indem die globale Transformation eines Graphics-Objekts festgelegt wird.
Matrix myMatrix = new Matrix(1, 0, 0, -1, 0, 0);
myGraphics.Transform = myMatrix;
myGraphics.TranslateTransform(200, 150, MatrixOrder.Append);
Dim myMatrix As New Matrix(1, 0, 0, -1, 0, 0)
myGraphics.Transform = myMatrix
myGraphics.TranslateTransform(200, 150, MatrixOrder.Append)
Der folgende Code (platziert am Ende des vorherigen Beispiels) erstellt einen Pfad, der aus einem einzelnen Rechteck mit seiner unteren linken Ecke am Ursprung des neuen Koordinatensystems besteht. Das Rechteck wird einmal ohne lokale Transformation und einmal mit einer lokalen Transformation gefüllt. Die lokale Transformation besteht aus einer horizontalen Skalierung um einen Faktor von 2, gefolgt von einer Drehung um 30 Grad.
// Create the path.
GraphicsPath myGraphicsPath = new GraphicsPath();
Rectangle myRectangle = new Rectangle(0, 0, 60, 60);
myGraphicsPath.AddRectangle(myRectangle);
// Fill the path on the new coordinate system.
// No local transformation
myGraphics.FillPath(mySolidBrush1, myGraphicsPath);
// Set the local transformation of the GraphicsPath object.
Matrix myPathMatrix = new Matrix();
myPathMatrix.Scale(2, 1);
myPathMatrix.Rotate(30, MatrixOrder.Append);
myGraphicsPath.Transform(myPathMatrix);
// Fill the transformed path on the new coordinate system.
myGraphics.FillPath(mySolidBrush2, myGraphicsPath);
' Create the path.
Dim myGraphicsPath As New GraphicsPath()
Dim myRectangle As New Rectangle(0, 0, 60, 60)
myGraphicsPath.AddRectangle(myRectangle)
' Fill the path on the new coordinate system.
' No local transformation
myGraphics.FillPath(mySolidBrush1, myGraphicsPath)
' Set the local transformation of the GraphicsPath object.
Dim myPathMatrix As New Matrix()
myPathMatrix.Scale(2, 1)
myPathMatrix.Rotate(30, MatrixOrder.Append)
myGraphicsPath.Transform(myPathMatrix)
' Fill the transformed path on the new coordinate system.
myGraphics.FillPath(mySolidBrush2, myGraphicsPath)
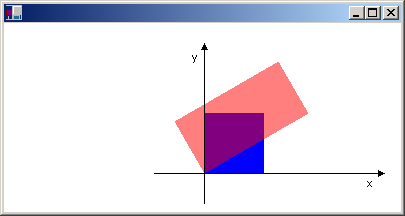
Die folgende Abbildung zeigt das neue Koordinatensystem und die beiden Rechtecke.
Siehe auch
.NET Desktop feedback
