Tutorial: Implementieren eines Quanten-Zufallszahlengenerators in Q#

In diesem Lernprogramm lernen Sie, ein grundlegendes Quantenprogramm zu schreiben, in Q# dem die Natur der Quantenmechanik genutzt wird, um eine Zufallszahl zu erzeugen.

In diesem Lernprogramm lernen Sie Folgendes:

• Erstellen Sie ein Q# Programm.
• Überprüfen Sie die Hauptkomponenten eines Q# Programms.
• Definieren Sie die Logik eines Problems.
• Kombinieren Sie klassische und Quantenoperationen, um ein Problem zu lösen.
• Arbeiten mit Qubits und Superposition, um einen Quanten-Zufallszahlen-Generator zu erstellen

Tipp

Wenn Sie Ihre Quantum Computing-Reise beschleunigen möchten, schauen Sie sich Code mit Azure Quantum an, einem einzigartigen Feature der Azure Quantum-Website. Hier können Sie integrierte Q# Beispiele oder Eigene Q# Programme ausführen, neuen Q# Code aus Ihren Eingabeaufforderungen generieren, Ihren Code in VS Code für das Web mit nur einem Klick öffnen und ausführen und Copilot fragen.

Voraussetzungen

• So führen Sie das Codebeispiel im Copilot in Azure Quantum aus:

  • Ein Microsoft-E-Mail-Konto (MSA).

• So entwickeln und führen Sie das Codebeispiel in Visual Studio Code aus:

  • Die neueste Version von Visual Studio Code oder öffnen Sie VS Code im Web.

  • Die neueste Version der Quantum Development Kit. Details zur Installation finden Sie unter Einrichten der QDK-Erweiterung.

  • Wenn Sie Jupyter-Notizbücher verwenden möchten, müssen Sie auch Pythonqsharp. Öffnen Sie dazu ein Terminal, und führen Sie den folgenden Befehl aus:

    $ pip install --upgrade  qsharp
    

Definieren des Problems

Klassische Computer erzeugen keine Zufallszahlen, sondern Pseudozufallszahlen. Ein Pseudozufallszahlen-Generator generiert eine deterministische Sequenz von Zahlen auf Grundlage eines Ausgangswerts, der als Seed bezeichnet wird. Um sich Zufallswerten besser anzunähern, ist dieser Ausgangswert oft die aktuelle Zeit der CPU-Uhr.

Quantencomputer hingegen können echte Zufallszahlen generieren. Dies liegt daran, dass die Messung eines Qubits in der Superposition ein probabilistischer Prozess ist. Das Ergebnis der Messung ist zufällig und es gibt keine Möglichkeit, das Ergebnis vorherzusagen. Dies ist das Grundprinzip von Quanten-Zufallszahlengeneratoren.

Ein Qubit ist eine Einheit von Quanteninformationen, die sich in der Superposition befindet. Bei der Messung kann sich ein Qubit entweder im Zustand 0 oder im Zustand 1 befinden. Vor der Messung stellt der Qubitzustand jedoch die Wahrscheinlichkeit dar, mit der bei einer Messung entweder 0 oder 1 gelesen wird.

Sie beginnen mit einem Qubit in einem Basiszustand, z. B. 0. Der erste Schritt des Zufallszahlengenerators besteht darin, einen Hadamard-Vorgang zu verwenden, um das Qubit in eine gleiche Superposition zu setzen. Die Messung dieses Zustands führt zu einer Null oder einer mit einer Wahrscheinlichkeit von 50 % jedes Ergebnisses, einem wirklich zufälligen Bit.

Es gibt keine Möglichkeit zu wissen, was Sie nach der Messung des Qubits in Superposition erhalten werden, und das Ergebnis ist bei jedem Aufruf des Codes ein anderer Wert. Aber wie können Sie dieses Verhalten verwenden, um größere Zufallszahlen zu generieren?

Angenommen, Sie wiederholen den Prozess viermal und erzeugen dabei diese Folge von Binärzahlen:

$${0, 1, 1, 0}$$

Wenn Sie diese Bits verketten oder in eine Bitzeichenfolge kombinieren, können Sie eine größere Zahl bilden. In diesem Beispiel entspricht die Bitfolge ${0110}$ der Dezimalzahl 6.

$${0110_{\ binary} \equiv 6_{\ decimal}}$$

Wenn Sie diesen Prozess mehrmals wiederholen, können Sie mehrere Bits zu einer beliebigen großen Zahl kombinieren. Mit dieser Methode können Sie eine Zahl erstellen, die als sicheres Kennwort verwendet werden soll, da Sie sicher sein können, dass kein Hacker die Ergebnisse der Abfolge der Messungen ermitteln konnte.

Definieren der Logik für den Zufallszahlen-Generator

Sehen wir uns an, was die Logik eines Zufallszahlengenerators sein sollte:

1. Definieren Sie max als höchste Zahl, die Sie generieren möchten.
2. Definieren Sie die Anzahl der Zufallsbits, die Sie generieren müssen. Dazu wird berechnet, wie viele Bits , nBitsSie ganze Zahlen bis zu maxausdrücken müssen.
3. Generieren Sie eine zufällige Bitzeichenfolge, die nBits lang ist.
4. Wenn die Bitzeichenfolge eine Zahl größer als max darstellt, kehren Sie zu Schritt 3 zurück.
5. Andernfalls ist der Vorgang abgeschlossen. Geben Sie die generierte Zahl als ganze Zahl zurück.

Legen Sie zum Beispiel max auf 12 fest. Das heißt, 12 ist die größte Zahl, die Sie als Kennwort verwenden möchten.

Sie benötigen ${\lfloor ln(12) / ln(2) + 1 \rfloor}$ gleich 4 Bits, um eine Zahl zwischen 0 und 12 darzustellen. Wir können die integrierte Funktion BitSizeIverwenden, die eine ganze Zahl akzeptiert und die Anzahl der Bits zurückgibt, die erforderlich sind, um sie darzustellen.

Angenommen, Sie generieren die Bitzeichenfolge ${1101_{\ binary}}$, dann entspricht dies ${13_{\ decimal}}$. Da 13 größer als 12 ist, wiederholen Sie den Vorgang.

Als Nächstes generieren Sie die Bitzeichenfolge ${0110_{\ binary}}$, dies entspricht ${6_{\ decimal}}$. Da 6 kleiner als 12 ist, ist der Prozess abgeschlossen.

Der Zufallszahlengenerator gibt zahl 6 als Kennwort zurück. Legen Sie in der Praxis eine größere Zahl als den Höchstwert fest, da niedrigere Zahlen einfach zu knacken sind, indem einfach alle möglichen Kennwörter ausprobiert werden. Um das Erraten oder Knacken des Kennworts weiter zu erschweren, könnten Sie den ASCII-Code verwenden, um Binärdaten in Text zu konvertieren und ein Kennwort mithilfe von Zahlen, Symbolen und einer Mischung aus Groß- und Kleinbuchstaben zu generieren.

Schreiben eines zufälligen Bitgenerators

Der erste Schritt besteht darin, einen Q# Vorgang zu schreiben, der ein zufälliges Bit generiert. Dieser Vorgang ist einer der Bausteine des Zufallszahlengenerators.

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Sehen Sie sich den neuen Code an.

• Sie definieren den GenerateRandomBit-Vorgang. Dieser benötigt keine Eingabe und erzeugt einen Wert vom Typ Result. Der Typ Result stellt das Ergebnis einer Messung dar und kann einen von zwei möglichen Werten haben: Zero oder One.
• Sie weisen ein einzelnes Qubit mit dem use Schlüsselwort zu. Wenn sie zugewiesen wird, befindet sich ein Qubit immer im Zustand "|0".
• Sie verwenden den H Vorgang, um das Qubit in einer gleichen Superposition zu platzieren.
• Sie verwenden den M Vorgang zum Messen des Qubits, zurückgeben den gemessenen Wert (Zero oder One).
• Sie verwenden den Reset Vorgang, um den Qubit auf den Zustand '|0' zurückzusetzen.

Wenn das Qubit mithilfe der H-Operation in Superposition versetzt und mithilfe der M-Operation gemessen wird, führt jeder Codeaufruf zu einem anderen Ergebniswert.

Visualisieren des Q# Codes mit der Bloch-Kugel

Bei der Bloch-Kugel steht der Nordpol für den klassischen Wert 0 und der Südpol für den klassischen Wert 1. Jede Überlagerung kann durch einen Punkt auf der Kugel dargestellt werden (per Pfeil). Je näher sich das Ende des Pfeils an einem der Pole befindet, desto höher ist die Wahrscheinlichkeit, dass das Qubit bei einer Messung auf den klassischen Wert zurückfällt, der dem Pol zugeordnet ist. Bei dem durch den Pfeil dargestellten Qubit-Zustand in der folgenden Abbildung ist es beispielsweise wahrscheinlicher, dass sich bei einer Messung der Wert 0 ergibt:

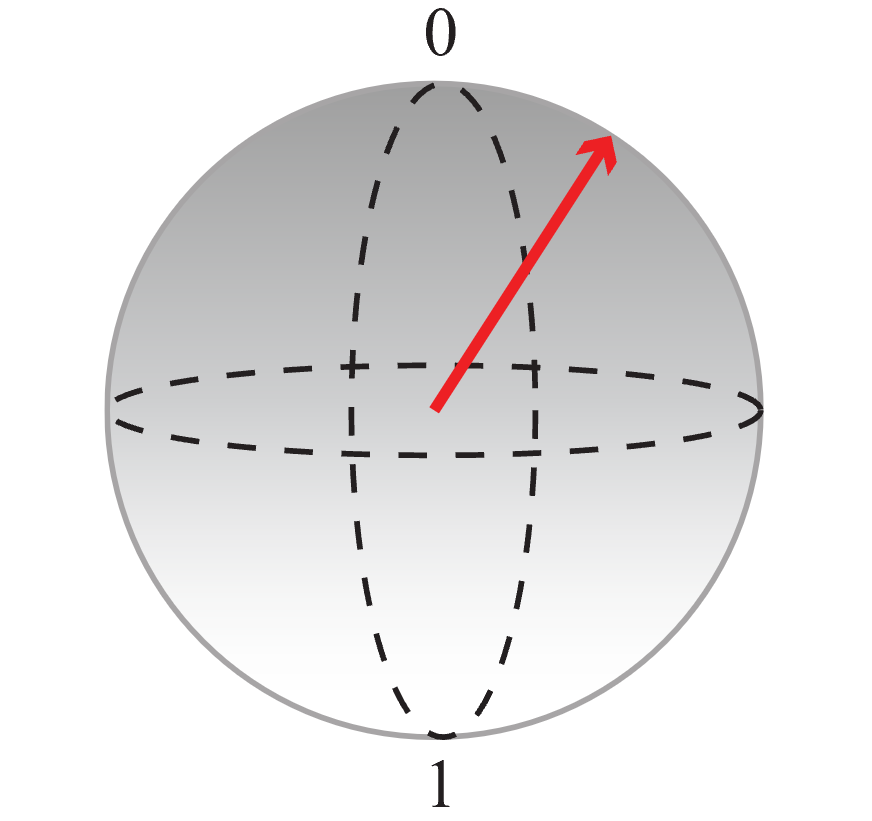
Diese Darstellung kann zur Visualisierung der Aktivitäten des Codes verwendet werden:

1. Beginnen Sie zunächst mit einem qubit initialisiert im |0-Zustand und wenden Sie einen H Vorgang an, um eine gleiche Superposition zu erstellen, in der die Wahrscheinlichkeiten für 0 und 1 identisch sind.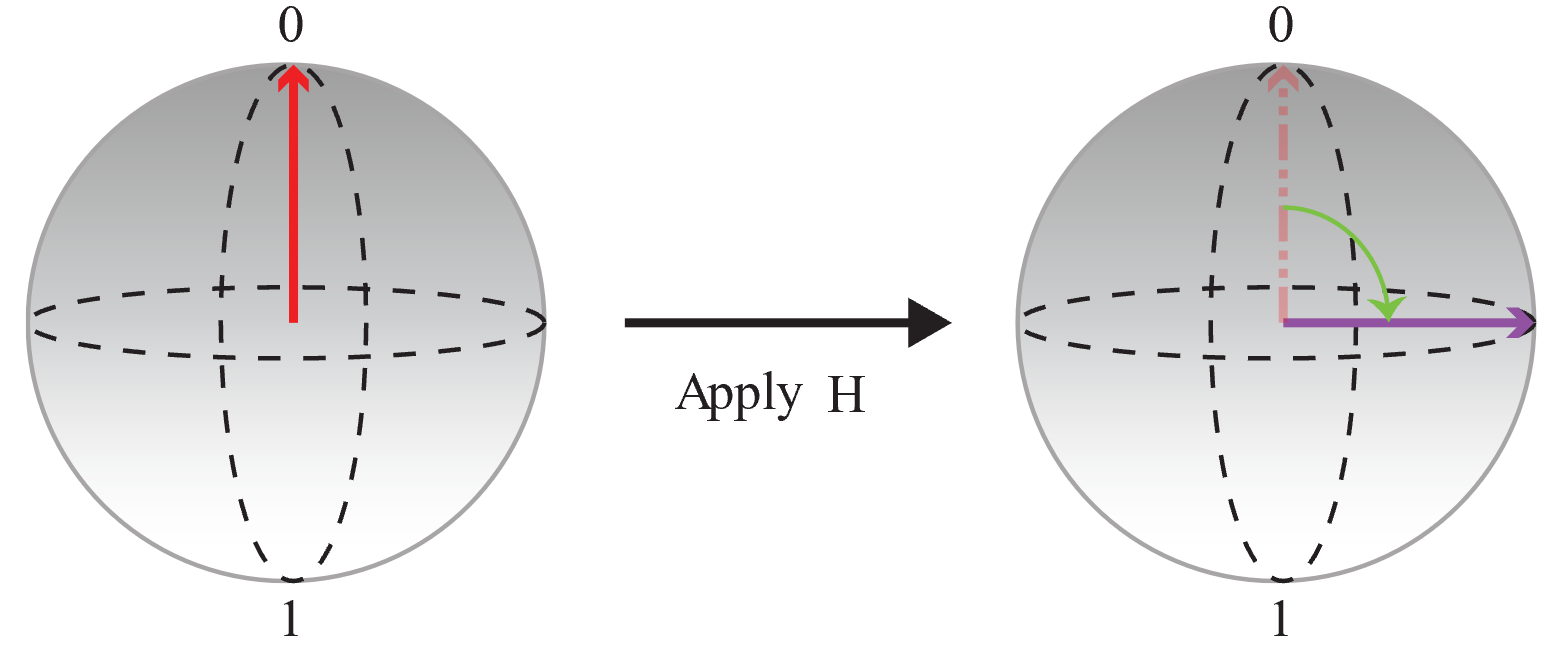

   

2. Messen Sie anschließend das Qubit, und speichern Sie die Ausgabe:

   

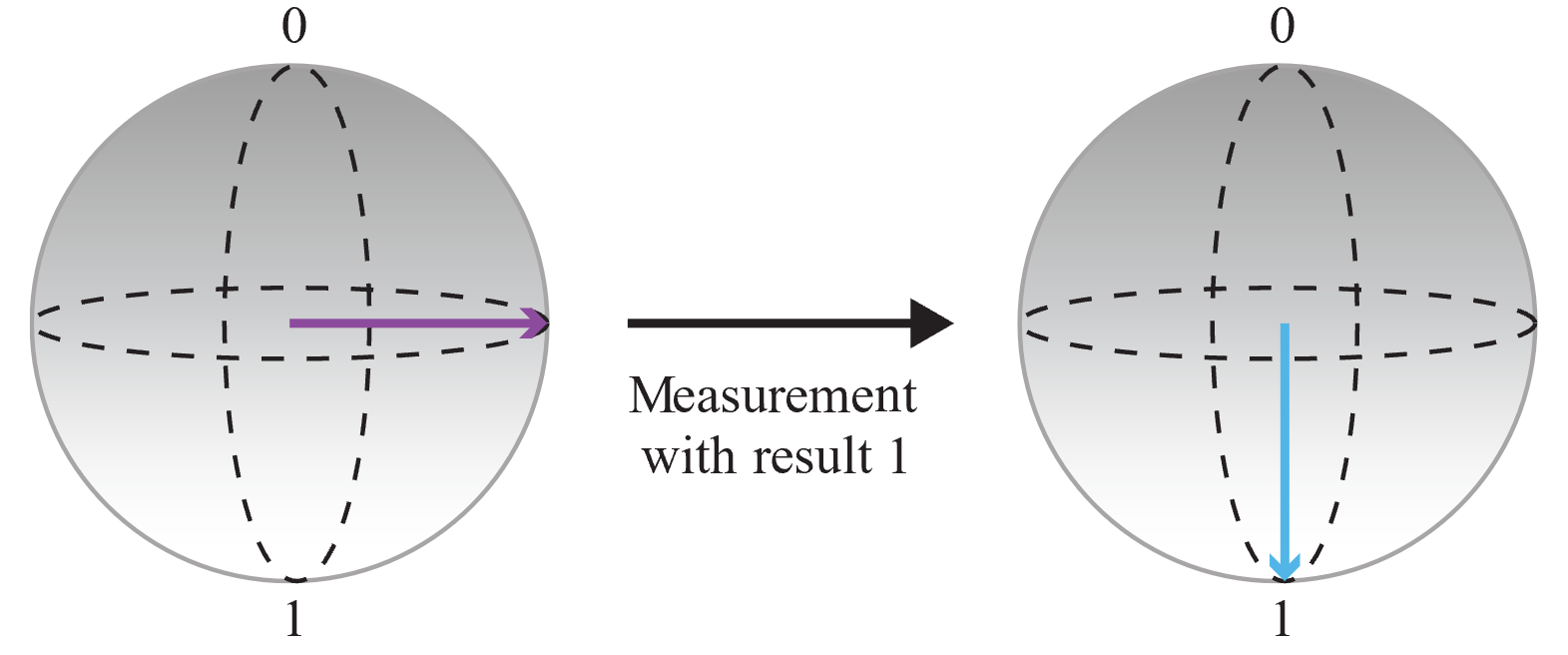
Da das Ergebnis der Messung zufällig und die Wahrscheinlichkeit der Messung von 0 oder 1 identisch ist, haben Sie ein vollkommen zufälliges Bit erhalten. Sie können diesen Vorgang mehrmals aufrufen, um ganze Zahlen zu erstellen. Wenn Sie den Vorgang beispielsweise dreimal aufrufen, um drei zufällige Bits zu erhalten, können Sie zufällige 3-Bit-Zahlen erstellen (also eine Zufallszahl zwischen 0 und 7).

Schreiben eines vollständigen Zufallszahlengenerators

1. Zunächst müssen Sie die erforderlichen Namespaces aus der Q# Standardbibliothek in das Programm importieren. Der Q# Compiler lädt viele allgemeine Funktionen und Vorgänge automatisch, aber für den vollständigen Zufallszahlengenerator benötigen Sie einige zusätzliche Funktionen und Vorgänge aus zwei Q# Namespaces: Microsoft.Quantum.Mathund Microsoft.Quantum.Convert.

   import Microsoft.Quantum.Convert.*;
   import Microsoft.Quantum.Math.*;
   

2. Als Nächstes definieren Sie den GenerateRandomNumberInRange Vorgang. Mit diesem Vorgang wird der GenerateRandomBit-Vorgang wiederholt aufgerufen, um eine Bitzeichenfolge zu erstellen.

   /// Generates a random number between 0 and `max`.
   operation GenerateRandomNumberInRange(max : Int) : Int {
       // Determine the number of bits needed to represent `max` and store it
       // in the `nBits` variable. Then generate `nBits` random bits which will
       // represent the generated random number.
       mutable bits = [];
       let nBits = BitSizeI(max);
       for idxBit in 1..nBits {
           bits += [GenerateRandomBit()];
       }
       let sample = ResultArrayAsInt(bits);
   
       // Return random number if it is within the requested range.
       // Generate it again if it is outside the range.
       return sample > max ? GenerateRandomNumberInRange(max) | sample;
   }
   
   

   Sehen Sie sich den neuen Code noch einmal an.

   • Sie müssen die Anzahl der Bits berechnen, die erforderlich sind, um ganze Zahlen bis zu maxausdrücken. Die BitSizeI Funktion aus dem Microsoft.Quantum.Math Namespace konvertiert eine ganze Zahl in die Anzahl der Bits, die erforderlich sind, um sie darzustellen.
   • Der SampleRandomNumberInRange-Vorgang verwendet eine for-Schleife zum Generieren von Zufallszahlen, bis eine Zahl generiert wird, die kleiner oder gleich max ist. Die for-Schleife funktioniert genauso wie eine for-Schleife in anderen Programmiersprachen.
   • Die Variable bits ist eine veränderbare Variable. Eine änderbare Variable ist eine Variable, die während der Berechnung geändert werden kann. Verwenden Sie die set-Direktive, um den Wert einer änderbaren Variablen zu ändern.
   • Die ResultArrayAsInt Funktion konvertiert aus dem Standardnamespace Microsoft.Quantum.Convert die Bitzeichenfolge in eine positive ganze Zahl.

3. Schließlich fügen Sie dem Programm einen Einstiegspunkt hinzu. Standardmäßig sucht der Q# Compiler nach einem Main Vorgang und startet die Verarbeitung dort. Er ruft den GenerateRandomNumberInRange Vorgang auf, um eine Zufallszahl zwischen 0 und 100 zu generieren.

   operation Main() : Int {
       let max = 100;
       Message($"Sampling a random number between 0 and {max}: ");
   
       // Generate random number in the 0..max range.
       return GenerateRandomNumberInRange(max);
   }
   

   Mit der let-Direktive werden Variablen deklariert, die während der Berechnung nicht geändert werden. Hier definieren Sie den Maximalwert als 100.

   Weitere Informationen zum Main Vorgang finden Sie unter "Einstiegspunkte".

4. Der vollständige Code für den Zufallszahlengenerator lautet wie folgt:

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using a Hadamard operation
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Ausführen des Programms für den Zufallszahlengenerator

Sie können das Programm im Copilot in Azure Quantum und in Visual Studio Code als eigenständige Q# Anwendung oder mit einem Python-Hostprogramm ausführen.

Copilot in Azure Quantum

Sie können Ihren Q# Code mit dem Copilot in Azure Quantum kostenlos testen – alles, was Sie benötigen, ist ein Microsoft-E-Mail-Konto (MSA). Weitere Informationen zum Copilot in Azure Quantum finden Sie unter Explore Azure Quantum.

1. Öffnen Sie den Copilot in Azure Quantum in Ihrem Browser.

2. Kopieren Sie den folgenden Code, und fügen Sie ihn in den Code-Editor ein.

   import Microsoft.Quantum.Convert.*;
   import Microsoft.Quantum.Math.*;
   
   operation Main() : Int {
       let max = 100;
       Message($"Sampling a random number between 0 and {max}: ");
   
       // Generate random number in the 0..max range.
       return GenerateRandomNumberInRange(max);
   }
   
   /// # Summary
   /// Generates a random number between 0 and `max`.
   operation GenerateRandomNumberInRange(max : Int) : Int {
       // Determine the number of bits needed to represent `max` and store it
       // in the `nBits` variable. Then generate `nBits` random bits which will
       // represent the generated random number.
       mutable bits = [];
       let nBits = BitSizeI(max);
       for idxBit in 1..nBits {
           bits += [GenerateRandomBit()];
       }
       let sample = ResultArrayAsInt(bits);
   
       // Return random number if it is within the requested range.
       // Generate it again if it is outside the range.
       return sample > max ? GenerateRandomNumberInRange(max) | sample;
   }
   
   /// # Summary
   /// Generates a random bit.
   operation GenerateRandomBit() : Result {
       // Allocate a qubit.
       use q = Qubit();
   
       // Set the qubit into superposition of 0 and 1 using the Hadamard 
       // operation `H`.
       H(q);
   
       // At this point the qubit `q` has 50% chance of being measured in the
       // |0〉 state and 50% chance of being measured in the |1〉 state.
       // Measure the qubit value using the `M` operation, and store the
       // measurement value in the `result` variable.
       let result = M(q);
   
       // Reset qubit to the |0〉 state.
       // Qubits must be in the |0〉 state by the time they are released.
       Reset(q);
   
       // Return the result of the measurement.
       return result;
   
       // Note that Qubit `q` is automatically released at the end of the block.
   }
   
   

3. Wählen Sie die Anzahl der auszuführenden Aufnahmen und dann "Ausführen" aus.

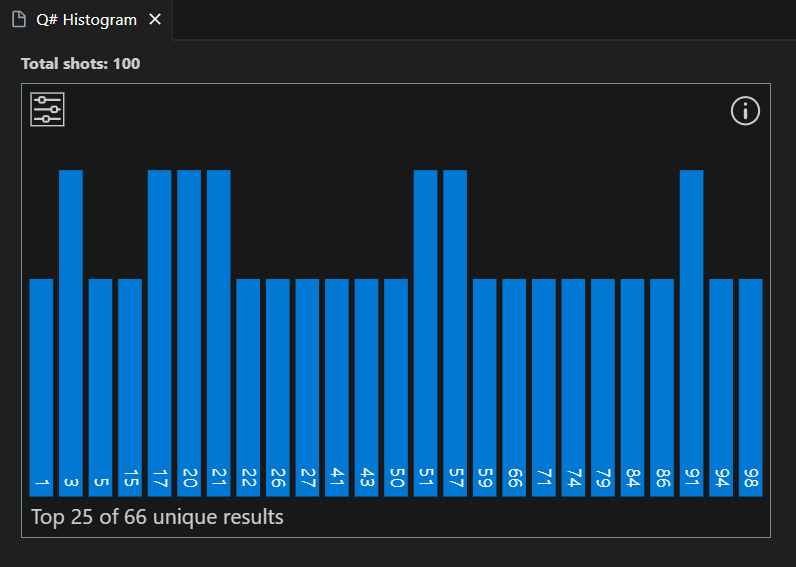
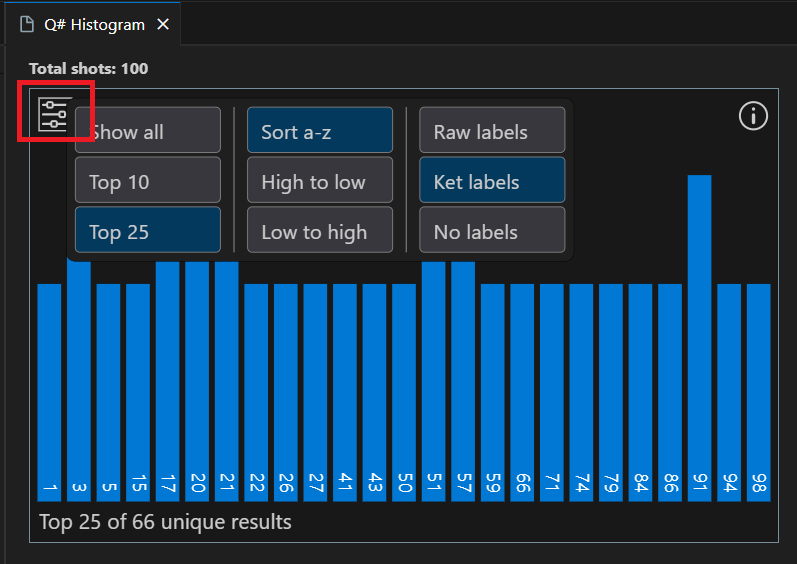
4. Die Ergebnisse werden im Histogramm und in den Feldern "Ergebnisse " angezeigt.

5. Wählen Sie "Erklären"-Code aus, um Copilot aufzufordern, den Code Ihnen zu erläutern.

Tipp

Über Copilot in Azure Quantum können Sie Ihr Programm in VS Code für das Web öffnen, indem Sie in der rechten Ecke des Code-Editors die Schaltfläche "VS Code-Logo" auswählen.

Q# Programm in Visual Studio Code

1. Öffnen Sie Visual Studio Code und wählen Sie Datei > Neue Textdatei aus, um eine neue Datei zu erstellen.

2. Speichern Sie die Datei unter dem Namen RandomNumberGenerator.qs. Diese Datei enthält den Q# Code für Ihr Programm.

3. Kopieren Sie den folgenden Code in der RandomNumberGenerator.qs Datei.

   
   import Microsoft.Quantum.Convert.*;
   import Microsoft.Quantum.Math.*;
   
   operation Main() : Int {
       let max = 100;
       Message($"Sampling a random number between 0 and {max}: ");
   
       // Generate random number in the 0..max range.
       return GenerateRandomNumberInRange(max);
   }
   
   /// # Summary
   /// Generates a random number between 0 and `max`.
   operation GenerateRandomNumberInRange(max : Int) : Int {
       // Determine the number of bits needed to represent `max` and store it
       // in the `nBits` variable. Then generate `nBits` random bits which will
       // represent the generated random number.
       mutable bits = [];
       let nBits = BitSizeI(max);
       for idxBit in 1..nBits {
           bits += [GenerateRandomBit()];
       }
       let sample = ResultArrayAsInt(bits);
   
       // Return random number if it is within the requested range.
       // Generate it again if it is outside the range.
       return sample > max ? GenerateRandomNumberInRange(max) | sample;
   }
   
   /// # Summary
   /// Generates a random bit.
   operation GenerateRandomBit() : Result {
       // Allocate a qubit.
       use q = Qubit();
   
       // Set the qubit into superposition of 0 and 1 using the Hadamard 
       // operation `H`.
       H(q);
   
       // At this point the qubit `q` has 50% chance of being measured in the
       // |0〉 state and 50% chance of being measured in the |1〉 state.
       // Measure the qubit value using the `M` operation, and store the
       // measurement value in the `result` variable.
       let result = M(q);
   
       // Reset qubit to the |0〉 state.
       // Qubits must be in the |0〉 state by the time they are released.
       Reset(q);
   
       // Return the result of the measurement.
       return result;
   
       // Note that Qubit `q` is automatically released at the end of the block.
   }
   
   

4. Bevor Sie das Programm ausführen, müssen Sie das target Profil auf "Uneingeschränkt" festlegen. Wählen Sie "Ansicht " - >, suchen Sie nach QIR, wählen Sie : Q#target fest, und wählen Sie Q#

5. Um Ihr Programm auszuführen, wählen Sie Q#" oben rechts die Option "Ausführen" aus, wählen Sie "Ausführen" aus der Liste der vorherigen Main()Befehle aus, oder drücken Sie STRG+F5. Das Programm führt den Main() Vorgang im Standardsimulator aus.

   

6. Die Ausgabe wird in der Debugkonsole angezeigt.

7. Führen Sie das Programm erneut aus, um ein anderes Ergebnis anzuzeigen.

Hinweis

Wenn das target Profil nicht auf "Uneingeschränkt" festgelegt ist, wird beim Ausführen des Programms eine Fehlermeldung angezeigt.

Zeichnen des Häufigkeits histogramms

Lassen Sie uns die Verteilung der Ergebnisse visualisieren, die aus der Ausführung des Quantenprogramms mehrmals erzielt werden. Das Häufigkeits histogramm hilft dabei, die Wahrscheinlichkeitsverteilung dieser Ergebnisse zu visualisieren.

1. Wählen Sie "Ansicht"> aus, und geben Sie "Histogramm" ein, das die Q#Option "Datei ausführen" anzeigt und die Option "Histogramm anzeigen" anzeigt. Sie können auch HistogrammMain(). Wählen Sie diese Option aus, um das Q# Histogrammfenster zu öffnen.

   

2. Geben Sie eine Reihe von Aufnahmen ein, um das Programm auszuführen, z. B. 100 Aufnahmen, und drücken Sie die EINGABETASTE. Das Histogramm wird im Q# Histogrammfenster angezeigt.

3. Jeder Balken im Histogramm entspricht einem möglichen Ergebnis, und seine Höhe stellt die Anzahl der Beobachteten dar. Die Anzahl der verschiedenen Ergebnisse kann bei jeder Ausführung des Histogramms unterschiedlich sein.

   

   Tipp

   Sie können das Histogramm mithilfe des Mausrads oder einer Trackpadgeste zoomen. Beim Vergrößern können Sie das Diagramm verschieben, indem Sie beim Scrollen die ALT-TASTE drücken.

4. Wählen Sie einen Balken aus, um den Prozentsatz dieses Ergebnisses anzuzeigen.

5. Wählen Sie das Symbol für die oberen linken Einstellungen aus, um Optionen anzuzeigen. Sie können top 10 Ergebnisse, top 25 Ergebnisse oder alle Ergebnisse anzeigen. Sie können die Ergebnisse auch von hoch bis niedrig oder niedrig bis hoch sortieren.

   

Jupyter-Notizbuch in VS-Code

1. Wählen Sie in VS Code die Optionen Ansicht > Befehlspalette und dann Erstellen aus: Verwenden von Jupyter Notebook.

2. Importieren Sie in der ersten Zelle das qsharp Paket in Ihrem Python-Code:

   import qsharp
   

3. Fügen Sie den Q# Code für das Quantum random number generator program hinzu. Dazu verwenden Sie den %%qsharp magischen Befehl. Beachten Sie, dass der %%qsharp Befehl die Notizbuchzelle vom Typ in den Typ PythonQ#ändert. Kopieren Sie diesen Code in die zweite Zelle.

   %%qsharp
   
   import Microsoft.Quantum.Convert.*;
   import Microsoft.Quantum.Math.*;
   
   operation Main() : Int {
       let max = 100;
   
       // Generate random number in the 0..max range.
       return GenerateRandomNumberInRange(max);
   }
   
   /// # Summary
   /// Generates a random number between 0 and `max`.
   operation GenerateRandomNumberInRange(max : Int) : Int {
       // Determine the number of bits needed to represent `max` and store it
       // in the `nBits` variable. Then generate `nBits` random bits which will
       // represent the generated random number.
       mutable bits = [];
       let nBits = BitSizeI(max);
       for idxBit in 1..nBits {
           bits += [GenerateRandomBit()];
       }
       let sample = ResultArrayAsInt(bits);
   
       // Return random number if it is within the requested range.
       // Generate it again if it is outside the range.
       return sample > max ? GenerateRandomNumberInRange(max) | sample;
   }
   
   /// # Summary
   /// Generates a random bit.
   operation GenerateRandomBit() : Result {
       // Allocate a qubit.
       use q = Qubit();
   
       // Set the qubit into superposition of 0 and 1 using the Hadamard 
       // operation `H`.
       H(q);
   
       // At this point the qubit `q` has 50% chance of being measured in the
       // |0〉 state and 50% chance of being measured in the |1〉 state.
       // Measure the qubit value using the `M` operation, and store the
       // measurement value in the `result` variable.
       let result = M(q);
   
       // Reset qubit to the |0〉 state.
       // Qubits must be in the |0〉 state by the time they are released.
       Reset(q);
   
       // Return the result of the measurement.
       return result;
   
       // Note that Qubit `q` is automatically released at the end of the block.
   }
   

4. Führen Sie schließlich den Code aus. Sie können dieselbe Simulation beliebig oft unabhängig ausführen. Jede unabhängige Simulation wird als "Shot" bezeichnet. Beispiel: Führen wir die Simulation 100 Mal aus.

   results = qsharp.run("Main()", shots=100)
   print(results)
   

Hinweis

Dieser Codeausschnitt wird derzeit nicht auf einer verfügbaren Azure Quantum-Hardware targetsausgeführt, da für den Aufruf ResultArrayAsInt eine QPU mit vollständigem Berechnungsprofil erforderlich ist.

Zugehöriger Inhalt

Sehen Sie sich weitere Q#-Tutorials an:

• Quantenanglement zeigt, wie ein Q# Programm geschrieben wird, das Qubits bearbeitet und misst und die Auswirkungen von Superposition und Veranglement veranschaulicht.
• Q# von Grover verwendet.
• Quantum Fourier Transforms untersucht, wie ein Q# Programm geschrieben wird, das direkt bestimmte Qubits adressiert.
• Die Quantum Katas sind selbstgesteuerte Lernprogramme und Programmierübungen, die darauf abzielen, die Elemente von Quantencomputing und Q# Programmierung gleichzeitig zu unterrichten.