Генерация случайных чисел с неравномерным распределением в C#
При создании симуляторов событий реального мира, или при генерации тестовых выборок для алгоритмов, которые будут использовать данные из реального мира, обычно очень полезно сгенерировать псевдослучайные числа с неравномерным законом распределения.
Я, наверное, уже потерял некоторых читателей, которые за столько времени уже забыли университетский курс STATS 101. А я – нет. Давайте сделаем шаг назад.
.NET Framework предоставляет удобный способ генерации псевдослучайных чисел в диапазоне от 0 до 1 с равномерным законом распределения. «Равномерное распределение» означает, что если разделить большой набор таких случайных чисел на два интервала, и в один поместить значения, большие 0.5, а в другой – меньшие 0.5, то мы получим примерно одинаковое количество чисел в каждом интервале, без перекоса в одну из сторон. Более того, если мы разделим те же самые значения на десять интервалов: 0.0-0.1, 0.1-0.2, 0.2-0.3 и т.д., то мы также не получим перекоса в одном из интервалов. На самом деле, не важно, на какое количество одинаковых интервалов мы разобьём данные, при достаточно большой выборке случайных чисел, в каждом интервале будет приблизительно равное количество элементов.
Вот что означает «равномерное распределение»: количество элементов в интервале пропорционально размеру интервала и не связано с его положением на отрезке. Я сгенерировал сто тысяч псевдослучайных чисел в диапазоне от 0 до 1, сгруппировал их в 50 интервалов и построил график количества элементов в каждом из них:

Это гистограмма. Как видите, каждый интервал содержит приблизительно 2% всех элементов, и не видно, чтобы какой-то из них заметно выделялся на общем фоне. Эта гистограмма показывает основную особенность равномерного распределения.
Теперь давайте рассмотрим отношение между формой графика и вероятностью. Предположим, мы выбрали одно случайное значение из ста тысяч. Какова вероятность того, что она будет в интервале 25? Очевидно, вероятность равна «высоте» интервала, деленой на общее количество значений. Но с точки зрения геометрии мы можем рассматривать эту вероятность, как площадь 25-го интервала деленную на общую площадь синей области.
Но обратили ли вы внимание на нечто неприятное в этом графике? Оси графика полностью определяются выбранными мной произвольными факторами. Давайте их нормализуем. Давайте переопределим горизонтальную ось, чтобы она представляла максимальное значение выбранного интервала. А как нам переопределить вертикальную ось? Как мы уже сказали, вероятность попадания определенного значения в определенный интервал пропорциональна его площади. Тогда давайте откалибруем ось так, чтобы вся площадь графика составляла 100% . Тогда ответом на вопрос: «какова вероятность того, что определенный элемент будет найден в таком-то интервале?» будет в точности равен площади этого интервала:

Данная нормализация обладает следующим замечательным свойством: она не зависит от того, какое количество случайных чисел мы сгенерируем, и не зависит от количества интервалов, на которые мы разобьём отрезок, гистограмма будет выглядеть более или менее одинаковой, оси будут одинаковыми. Распределение на обеих осях будет от 0 до 1 и вся площадь всегда будет равна 100%.
Теперь давайте представим, что произойдет в граничном случае. Предположим, мы будем продолжать генерировать случайные числа, и получим триллионы значений. И будем разбивать на все меньшие и меньшие интервалы. И если вы достаточно наблюдательны, то сможете сразу же сказать, что мы получим непрерывный график в виде простой прямой.

И вот, мы получили график непрерывного равномерного распределения. Но, естественно, это не единственное существующее распределение! Существует еще знаменитое «нормальное» или гауссово распределение. Диапазон нормального распределения является бесконечным с обоих концов; случайное значение, распределенное по нормальному закону, может иметь любое значение – положительное или отрицательно. Вот картинка из Википедии с четырьмя разными вариантами гауссова распределения:

Помните, что этот график можно рассматривать как частный случай гистограммы с бесконечным количеством данных и интервалов. В данном случае, опять-таки, вероятность нахождения значения в определенном интервале пропорциональна его площади. И, конечно же, площадь для каждого графика составляет 100%, вот почему более «худой» колокольчик выше широкого. И еще обратите внимание на то, что в каждом случае большая часть площади приходится на область в районе пика. Нормальное распределение является «вытянутым вверх, с длинными хвостами».
Существуют и другие законы распределения. Например, распределение Коши, тоже напоминает колокол, но в отличие от нормального распределение является более «широким». Вот четыре распределения Коши из Википедии:

Обратите внимание, насколько более пологими являются хвосты распределения, и насколько «колокол» стал уже, чтобы суммарная площадь осталась неизменной.
Однако с этими графиками что-то нет так, правда? Поскольку вероятность пропорциональна площади под кривой, то реальное значение кривой в определенной точке не является таким уж полезным. Другой характеристикой случайного распределения является вычисление вероятности того, что случайное число окажется, равно или меньшего заданного, т.е. площадь под кривой, меньшего заданного значения. Площадь под кривой является интегралом, так что давайте нарисуем его. Мы знаем, что кривая будет монотонно возрастать, и слева она стремится к нулю, а справа – к единице, поскольку вероятность получения очень и очень маленького значения близка к нулю, а вероятность получения числа, меньшего чем самое большое значение, стремится к 100%. Если мы построим график интегралов четырех распределений Коши, то получим следующее:
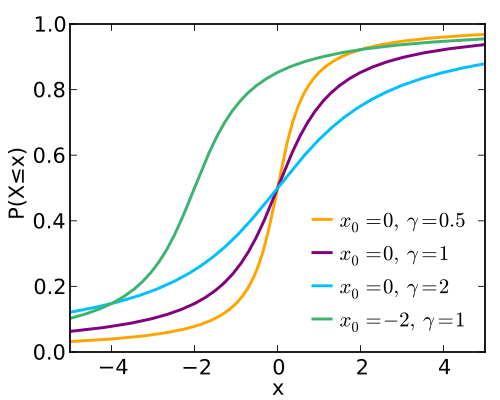
Этот график называется функцией распределения и только посмотрите, насколько легко его читать! Давайте рассмотрим фиолетовый график; ясно, что вероятность получить значение, равное или меньшее двум равняется примерно 85%; мы можем читать этот график. Этот график содержит ту же самую информацию, что график плотности вероятности; но он проще для понимания. Из исходного графика было довольно сложно понять, что 85% площади кривой приходилось на значения, меньшие 2.
Кстати, я упомянул, что наша функция является монотонно возрастающей, а значит, мы можем ее инвертировать. Давайте поменяем оси x и y местами:

Эта функция, которая является обратной к интегралу функции распределения, называется функцией квантилей. Она определяет «для вероятности p, заключенной в интервале от нуля до единицы, каково значение x, при котором вероятность получения случайного значения, меньшего x была бы равна p?» Этот график должен быть знаком всем, кто изучал тригонометрию в старших классах; функция квантилей распределения Коши – это просто функция тангенса, смещенная в интервал от нуля до единицы вместо стандартного интервала от -π / 2 до π / 2.
Что ж, это здорово. Кривая Коши это всего лишь производная от функции арктангенса. Ну и что? Что из этого?
Мы начали эти невероятные приключения с того, что хотели сгенерировать случайные числа с неравномерным законом распределения. Приведенные выше графики преобразовывают случайные числа с равномерным распределением, в случайные числа с распределением Коши. Это невероятно, но факт. Вот смотрите:
private static Random random = new Random();
private static IEnumerable<double> UniformDistribution()
{
while (true) yield return random.NextDouble();
}
private static double CauchyQuantile(double p)
{
return Math.Tan(Math.PI * (p - 0.5));
}
private static int[] CreateHistogram(IEnumerable<double> data, int buckets, double min, double max)
{
int[] results = new int[buckets];
double multiplier = buckets / (max - min);
foreach (double datum in data)
{
double index = (datum - min) * multiplier;
if (0.0 <= index && index < buckets)
results[(int)index] += 1;
}
return results;
}
И теперь вы можете объединить все вместе:
var cauchy = from x in UniformDistribution() select CauchyQuantile(x);
int[] histogram = CreateHistogram(cauchy.Take(100000), 50, -5.0, 5.0);
И если построите гистограмму, то естественно, получите распределение Коши:

Итак, подводим итог: если вам нужно получить случайные числа с некоторым законом распределения, все что вам нужно, это:
- найти нужную функцию распределения, чтобы площадь под кривой равнялась вероятности попадания случайного значения в этот диапазон,
- проинтегрировать функцию распределения для получения интегральной функции распределения,
- проинвертировать интегральную функцию распределения для получения функции квантилей и
- преобразовать равномерно распределенный набор данных с помощью функции квантилей,
Вот и все. Очень просто!
В следующий раз: небольшая загадка, основанная на приведенном выше коде.