Project Scheduling and Solver Foundation: links and constraints

Yesterday I introduced a simple OML model for computing project schedules.  The model has the following sections:

• Parameters: input data that comes from Excel.
• Decisions: the values that I want to solve for.
• Constraints: the relationships that decisions and parameters need to satisfy.
• Goals: the objective - what I want to optimize.

The exciting cliffhanger from my previous post was to model precedence links.  Let's think about how I could specify the links in Excel.  One way to do it is to have a table that simply lists the "predecessor" and "successor" tasks.  For example:

Pred	Succ
0	1
1	2

The first row says that task 0 is the predecessor of task 1, i.e. task 1 should start after task 0 finishes.  If we want to bind this data to our model, we should introduce a Set and a Parameter, just like we did for Tasks:

   Parameters[Sets, Links],
  Parameters[Integers, Pred[Links], Succ[Links]],

The domain for Pred and Succ is Integers because the table stores indexes for the tasks.  Now I need to change the model to enforce the links.  That's a constraint, which is expressed straightforwardly using a Foreach:

     Foreach[{l, Links}, Start[Succ[l]] >=Finish[Pred[l]] ]

If I setup the data binding for Links and re-solve, then I will see that the links are honored.  If you compare to Project's schedule, you may spot a problem: some of the tasks (for example t3) are scheduled later than they are in Project.  This is totally valid according to our model - t3 has "slack" and can move around without affecting the project schedule.  Think about how you could fix up the model to match Project, so that all tasks are scheduled "as soon as possible".

On to the "extra credit" problem: how to model "start no earlier than" (SNET) constraints.  This is actually not too hard if we just consider the SNET date to be another parameter just like Duration.  The constraint is straightforward:

   Parameters[Reals, SNET[Tasks]],
  Constraints[ Foreach[{t, Tasks}, Start[t] >= SNET[t] ]]

In my Excel spreadsheet, I added a SNET column with the date for the constraint for each task.  If a task does not have a SNET constraint, I just fill in a dummy date (e.g. 1/1/2009).  But I need a number, not a date, so in the adjacent column I add the formula "=C2-TODAY()" to give me the number of days since the project start date.  That's what I want to bind to.

For reference, here is the data in my spreadsheet:

 

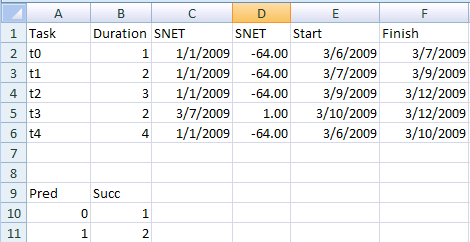
And here are the data bindings I created using the "Binding" button in the Solver Foundation ribbon:

 

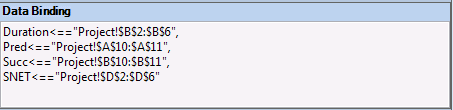
If you've been working with the spreadsheet, you may have been annoyed by a couple of things:

• If I add new tasks, I need to change the data binding to include the new cells.
• The conversion between dates and numbers is kind of bothersome.
• This is getting complicated.  For example, Project has eight different constraint types.  If I wanted to model them all the same way I modeled SNET, I would need to add a whole bunch of spreadsheet columns. 

Maybe it's time to turn this OML model into a C# program that directly calls Solver Foundation Services to model and solve project schedules.  Next time we will do just that.

Comments

• Anonymous
  March 16, 2009
  Nathan, I am working an a project that needs Project Scheduling calculations. Basically a function that will receive a set of activities / tasks / subtastks with relationships, contraints etc. The function needs to calculate the start, enddates, durations and lag. Please help find me one before I start writting the code myself. I need the code in C#

• Anonymous
  March 31, 2009
  Two weeks back I posted two articles showing how easy it is to model critical path scheduling using Microsoft