Curves on a Round Earth
Hi Folks,
When we talk about lines on the Earth, we don't really mean straight lines: we following the surface of the Earth, and that is inherently curved. Instead, when we talk about lines we mean great circles (or more precisely great elliptic arcs).
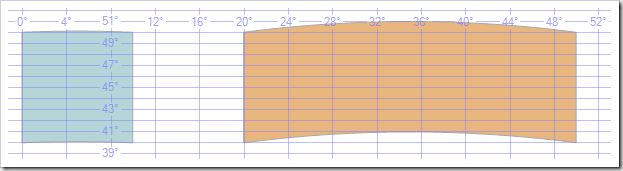
This choice of curve is the most natural one, I think, but it isn't always what we want. Take, for example, the US-Canada border, or at least the portion of it that follows the 49th parallel. Except for the equator, parallels are not great circles, but small circles. This means that a linestring for the border along 49th parallel cannot be described by a single simple edge, since that edge will diverge from the parallel. The longer these edges are, the greater the effect:
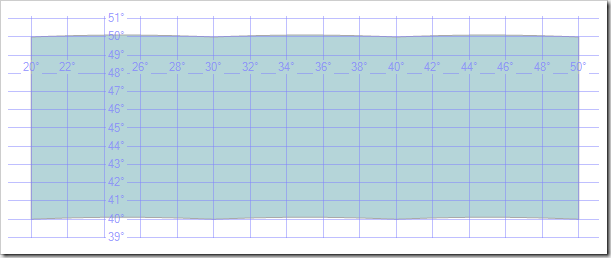
To keep this in check, you can add more control points. You'll never be able to describe this exactly with great circles, but the more you add, the closer you'll be:
In theory, there is nothing that prevents us from representing these small circles exactly, we just don't do so yet. Parallels (and general small circles) fall into the category of "curve support", which we may look at for the next release.
Another interesting type of curve is the rhumb line. These are used for navigation, and are key to the Mercator projection. (This came up on the forum recently, and I also mention them in my recent white paper.)
As always, if support for any of these---or any other type of curve---is of interest to you, you should drop us a feature request through Connect. There is a Connect request for rhumb lines, so you should vote there if you're interested. Surprisingly, I don't yet see one for parallels.
Cheers,
-Isaac