Resultater fra modeller til maskinel indlæring
Denne artikel beskriver forvekslingsmatrixer, klassificeringsproblemer og nøjagtighed inden for maskinel indlæringsmodeller (ML). Formålet er at forbedre din forståelse for nøjagtighed i ML-forudsigelsesresultater. Målgruppen omfatter ingeniører, analytikere og ledere, der vil opbygge deres viden og færdigheder inden for datavidenskab.
Forvekslingsmatrix
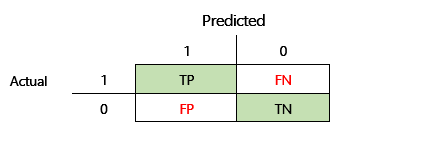
Når et overvåget ML-problem oplæres i et sæt historiske data, testes de ved hjælp af data, der tilbageholdes fra uddannelsesprocessen. På denne måde kan du sammenligne forudsigelser fra den uddannede model med de faktiske værdier. Forvekslingsmatrixen er en metode til at evaluere, hvor vellykkede et klassifikationsproblem er, og hvor det medfører fejl (dvs. hvor det bliver "forvirret").
Din målsætning kan f.eks. være at forudsige, om et kæledyr er en hund eller en kat, baseret på nogle fysiske og funktionsmæssige attributter. Hvis du har et test-datasæt, der indeholder 30 hunde og 20 katte, kan forvekslingsmatrixen ligne følgende illustration.
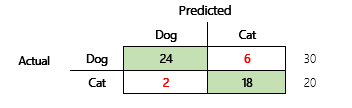
Tallene i de grønne celler viser korrekte forudsigelser. Som du kan se, har modellen forventet en højere procentdel for katte. Det er let at beregne den overordnede nøjagtighed af modellen. I dette tilfælde er det 42 ÷ 50 eller 0,84.
Multiklasse-klassificeringer i en forvekslingsmatrix
De fleste diskussioner om forvekslingsmatrixen er fokuseret på binære klassificeringer som i det foregående eksempel. Dette er et særligt tilfælde, hvor der kan tages højde for andre målinger, f. eks. følsomhed og tilbagekaldelse.
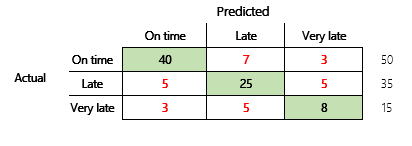
Derefter vil vi overveje et klassifikationsproblem for et økonomisk scenario, der har tre tilstande. Modellen bruges til at forudsige, om en debitorfaktura vil blive betalt til tiden, for sent eller meget for sent. Der betales f. eks. ud af 100 testfakturaer, 50 til tiden, 35 betales forsinket, og 15 betales meget for sent. I dette tilfælde kan en model oprette en forvekslingsmatrix, der ligner følgende illustration.
 ]
]
En forvekslingsmatrix giver betydeligt flere oplysninger end en simpel præcisionsmetrik. Men det er stadig forholdsvis let at forstå. En forvekslingsmatrix fortæller dig, om du har et afstemt datasæt, hvor outputklasserne har samme antal. I multiklasse-scenariet får du at vide, hvor langt du er fra en forudsigelse, når outputklasserne er ordenstal, som i ovenstående eksempel på kundebetalinger.
Modelnøjagtighed
De forskellige nøjagtighedsmålinger har fordelen ved at kvantificere modelkvaliteten.
Da nøjagtigheden er en nem metrikværdi for at forstå, er det et godt udgangspunkt at forklare en model til andre personer, især for brugerne af den model, der ikke er dataforskere. Det er ikke nødvendigt at forstå statistikken for at forstå modellens nøjagtighed. Når en forvekslingsmatrix er tilgængelig, giver den yderligere indblik i modellens præstation.
For at opnå en mere indgående forståelse bør der blive noteret flere udfordringer, der er forbundet med nøjagtigheden. Metrikværdiens anvendelighed afhænger af problemets kontekst. Et spørgsmål, der ofte opstår i forbindelse med modellens ydeevne er, "hvor god er modellen?" Svaret på dette spørgsmål er dog ikke nødvendigvis ligetil. Overvej følgende forvekslingsmatrix (model 2).
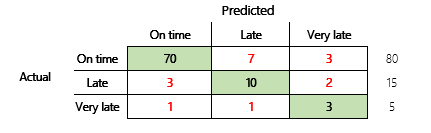
En hurtig beregning viser, at denne models nøjagtighed er (70 + 10 + 3) ÷ 100 eller 0,83. På overfladen virker dette resultat bedre end resultatet for den tidligere multiklasse-model (model 1), som har en nøjagtighed på 0,73. Men er det bedre?
Hvis du vil begynde at løse dette problem, skal du overveje nøjagtigheden af et naivt gæt. For at få et klassifikationsproblem vil et simpelt gæt altid forudsige den mest almindelige klasse. I model 1 vil det gæt være "til tiden", og det vil give en nøjagtighed på 0,50. Gættet i model 2 vil også være "til tiden", og det vil give en nøjagtighed på 0,80. Da model 1 forbedrer det naive gæt med 0,73 – 0,50 = 0,23, hvorimod model 2 forbedrer det naive gæt på 0,83 – 0,80 = 0,03, kan model 1 være en bedre model, selvom den har lavere nøjagtighed. I beregningen fremgår det, at en effektiv vurdering af en models kvalitet kræver mere kontekst end præcisionsværdien.
Et andet aspekt er også værd at bemærke. Tænk på et scenarie, hvor en medicinsk test bruges til at registrere en sygdom hos en patient. Dette problem er et binært klassifikationsproblem, hvor et positivt resultat viser, at patienten har sygdommen. I dette scenarie skal du overveje følgende fejl:
- Falske positivværdier, hvor testen viser, at der er tale om, at patienten har en sygdom, men patienten har ikke alligevel sygdommen.
- Falske negativværdier, hvor testen viser, at der er tale om, at patienten ikke har en sygdom, men patienten har alligevel sygdommen.
Det kan naturligvis være, at begge fejltyper er uønskede, men hvad er det værste? Det afhænger igen af omstændighederne. Hvis der er tale om en livstruende sygdom, der kræver hurtig behandling, har det højere prioritet at minimere falske negativer (som forhåbentligt efterfølges af yderligere test). I andre tilfælde, hvor der er tale om mindre kritiske situationer, kan modeloprettelser minimere falske positiver i stedet. Når det sker, er det en rimelig konklusion, at du skal have flere oplysninger end en nøjagtighedsmetrikværdi, hvis du effektivt skal kunne bestemme en models kvalitet.
Anbefalinger
Nøjagtigheden er et vigtigt værktøj til kommunikation med domæneeksperter, der ikke er fortrolige med statistikker. Men hvis oplysningerne skal gøres nyttige, er det vigtigt, at yderligere kontekst angives sammen med præcisionsværdien.
I forbindelse med betalingsprognosescenariet kan du angive et mål for den ML-model, der indeholder faktorer i forskellige betalingsmåder. Målet er, at modellen skal forbedres efter et naivt gæt ved at reducere antallet af forkerte svar med mindst 50 %. Med andre ord skal du bruge en nøjagtighed på målet, der adskiller sig mellem nøjagtigheden af et naivt gæt og 100 procent.
I følgende tabel opsummeres dette princip for forvekslingsmatrixer i denne artikel.
| Model | Naivt gæt | Målsætning | Modelnøjagtighed | Er målet opfyldt? |
|---|---|---|---|---|
| Model 1 | 0.50 | 0.75 | 0.73 | Næsten. Denne model forbedres betydeligt ved et gæt. |
| Model 2 | 0.80 | 0.90 | 0.83 | Nej Der kræves en forbedring. |
Nøjagtighed i F1-klassifikation
Den endelige overvejelse i denne artikel er en mere avanceret måleenhed med en overskredet ydeevne, der kaldes F1-nøjagtighed.
Før der kan defineres en nøjagtighed på F1, skal der angives to yderligere målepunkter: Præcision og tilbagekaldelse. Præcision angiver, hvor mange af det samlede antal forudsigelser, der er angivet som positive, der er korrekt tildelt. Denne metrikværdi kaldes også for den positive forudsigelige værdi. Tilbagekaldelse er det samlede antal af faktiske positive sager, der blev forudsagt korrekt. Denne metrikværdi kaldes også følsomhed.
I forvekslingsmatricen i ovenstående illustration beregnes disse målepunkter på følgende måde:
- Præcision = TP ÷ (TP + FP)
- Tilbagekald = TP ÷ (TP + FN)
Med F1-målpunktet kombineres præcision og tilbagekaldelse. Resultatet er den harmoniske middelværdi af de to værdier. Den beregnes på følgende måde:
- F1 = 2 × (præcision × tilbagekaldelse) ÷ (præcision + tilbagekaldelse)
Lad os se på et konkret eksempel. Tidligere i denne artikel var der et eksempel på en model, der forudsagde, om et dyr var en hund eller en kat. Illustrationen gentages her.
Her er resultatet, hvis "hund" bruges som det positive svar.
- Præcision = 24 ÷ (24 + 2) = 0,9231
- Tilbagekald = 24 ÷ (24 + 6) = 0,8
- F1 = 2 × (0,9231 × 0,8) ÷ (0,9231 + 0,8) = 0,8572
Som du kan se, er F1-værdien mellem værdierne for præcision og tilbagekaldelse.
Selvom det ikke er så nemt at forstå F1, tilføjer det en nuance til det grundlæggende nøjagtighedsnummer. Det kan også hjælpe med oplysninger, der ikke stemmer, som følgende diskussion viser.
Afsnittet Modelpræcision i denne artikel sammenlignede følgende to forvekslingsmatrixer. Selvom den første model havde lavere nøjagtighed, blev den vurderet til at være en mere nyttig model, da den viste en større forbedring end standardgættet for betaling til tiden.


Lad os se, hvordan disse to modeller sammenlignes, når F1-scoren bruges. F1-scorefaktorerne i præcision og tilbagekaldelse for hver tilstand, og F1-makroberegningen beregner derefter F1-scoren på tværs af tilstandene for at fastlægge et samlet antal F1-resultater. Der er andre F1-varianter, men det er af stor interesse at overveje makroversionen med den tilsvarende overvejelse, der er tildelt alle tre tilstande.
For at forenkle beregningerne blev eksempelmatricer bygget til at matche de faktiske og forudberegnede værdier. Disse matricer brugte sklearn i Python til at beregne værdierne. Her er resultatet.
| Model | Naivt gæt | Nøjagtighed | F1 makro |
|---|---|---|---|
| Model 1 | 0.5 | 0.73 | 0.67 |
| Model 2 | 0.80 | 0.83 | 0.66 |
Yderligere oplysninger om, hvordan denne beregning fungerer illustreres her i en sklearn.metrics-klassifikationsrapport for model 1. De tre tilstande, "Til tiden", "Sent" og "Meget sent" repræsenteres af de rækker, der kaldes henholdsvis 1, 2 og 3. Makrogennemsnittet er blot gennemsnittet af kolonnen "F1-score".
| præcision | tilbagekald | f1-score | |
|---|---|---|---|
| 1 | 0.83 | 0.80 | 0.82 |
| 2 | 0.68 | 0.71 | 0.69 |
| 3 | 0.50 | 0.50 | 0.50 |
Som disse resultater viser, har de to modeller næsten identiske præcisionsresultater for makroen F1. I dette og mange andre tilfælde viser F1 præcision en bedre indikator for en models kapacitet. Af hensyn til nøjagtigheden kræver fortolkningen af resultaterne, at du forstår, hvad der er vigtigst at overveje i modellen.