Analýza klasifikace s charakteristickými křivkami operátoru přijímače
Klasifikační modely musí přiřadit ukázku ke kategorii. Musí například používat funkce, jako je velikost, barva a pohyb, aby bylo možné určit, jestli je objekt pěší turistikou nebo stromem.
Klasifikační modely můžeme v mnoha ohledech vylepšit. Můžeme například zajistit, aby byla naše data vyvážená, čistá a škálovaná. Můžeme také změnit architekturu modelu a pomocí hyperparametrů zmáčknout tolik výkonu, kolik můžeme z dat a architektury. Nakonec nenajdeme lepší způsob, jak zlepšit výkon v naší sadě testů (nebo vydržet) a deklarovat náš model připravený.
Ladění modelu pro tento bod může být složité, ale můžeme použít poslední jednoduchý krok k dalšímu vylepšení toho, jak dobře náš model funguje. Abychom to ale pochopili, musíme se vrátit k základům.
Pravděpodobnosti a kategorie
Mnoho modelů má několik fází rozhodování a poslední je často jen krok binarizace. Během binarizace se pravděpodobnosti převedou na pevný popisek. Řekněme například, že model je poskytován s funkcemi a počítá, že existuje 75% pravděpodobnost, že se zobrazil pěší turista, a 25% pravděpodobnost, že se zobrazil strom. Objekt nemůže být 75% pěší a 25% strom; je to jeden nebo druhý! Model proto použije prahovou hodnotu, která je obvykle 50 %. Vzhledem k tomu, že třída pěší turistiky je větší než 50 %, objekt je deklarován jako pěší turistika.
50% prahová hodnota je logická; to znamená, že nejpravděpodobnější popisek podle modelu je vždy zvolen. Pokud je však model zkreslený, nemusí být tato 50% prahová hodnota vhodná. Pokud má například model mírnou tendenci vybírat stromy více než turisté, výběr stromů o 10 % častěji, než by měl, můžeme upravit prahovou hodnotu pro toto rozhodnutí.
Refresher on decision matrices
Rozhodovací matice představují skvělý způsob, jak vyhodnotit druhy chyb, které model provádí. To nám dává míru pravdivě pozitivních výsledků (TP), pravdivě negativních výsledků (TN), falešně pozitivních výsledků (FP) a falešně negativních výsledků (FN).

Některé užitečné charakteristiky můžeme vypočítat z konfuzní matice. Dvě oblíbené charakteristiky jsou:
- Pravdivá kladná míra (citlivost): jak často jsou popisky True správně identifikovány jako True. Například jak často model predikuje "hiker", když je zobrazený vzorek ve skutečnosti pěší turistika.
- Falešně pozitivní míra (míra falešně alarmů): jak často jsou popisky False nesprávně identifikovány jako True. Například jak často model predikuje "hiker", když se zobrazuje strom.
Když se podíváme na pravdivě pozitivní a falešně pozitivní míra, pomůže nám to pochopit výkon modelu.
Představte si náš příklad pěší turistiky. V ideálním případě je pravdivě pozitivní míra velmi vysoká a falešně pozitivní míra je velmi nízká, protože to znamená, že model identifikuje dobře pěší turistiku a velmi často neidentifikuje stromy jako pěší turistiku. Přesto, pokud je pravdivá pozitivní míra velmi vysoká, ale falešně pozitivní míra je také velmi vysoká, pak model je zkreslený; identifikuje téměř vše, co se setká jako pěší turistika. Podobně nechceme model s nízkou skutečnou kladnou rychlostí, protože když se model setká s pěší turistikou, označí je jako strom.
Křivky ROC
Křivky charakteristické operátorem přijímače (ROC) jsou graf, ve kterém vykreslují skutečnou kladnou rychlost a falešně pozitivní rychlost.
Křivky ROC mohou být matoucí pro začátečníky ze dvou hlavních důvodů. Prvním důvodem je, že začátečníki vědí, že model má pouze jednu hodnotu pro skutečné kladné a skutečné záporné sazby, takže graf ROC musí vypadat takto:
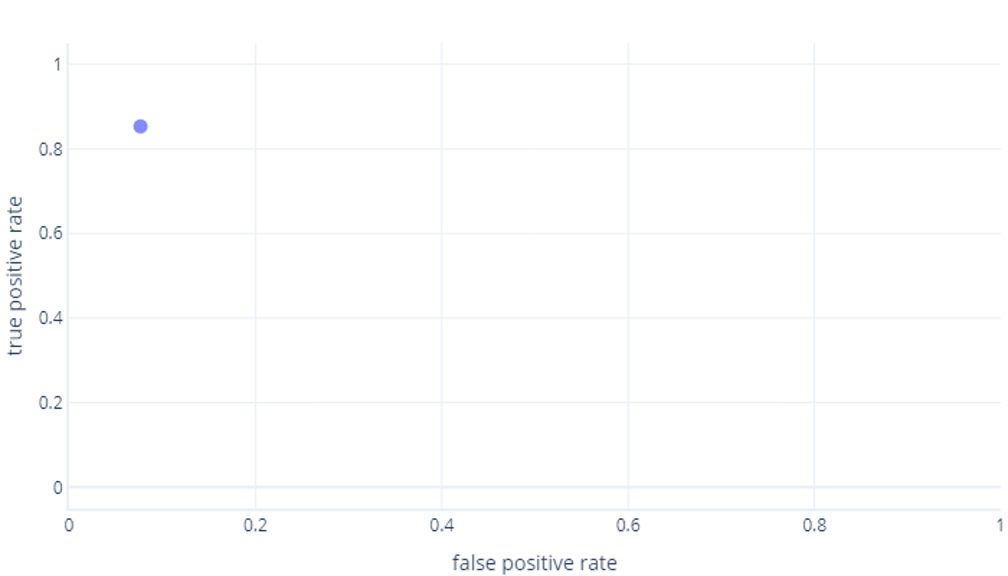
Jestli si to taky myslíš, máš pravdu. Vytrénovaný model vytvoří pouze jeden bod. Mějte ale na paměti, že naše modely mají prahovou hodnotu (obvykle 50 %), která se používá k rozhodnutí, jestli se má použít skutečný popisek (pěší turistika) nebo nepravda (strom). Pokud tuto prahovou hodnotu změníme na 30 % a přepočítáme pravdivě pozitivní a falešně pozitivní sazby, získáme další bod:
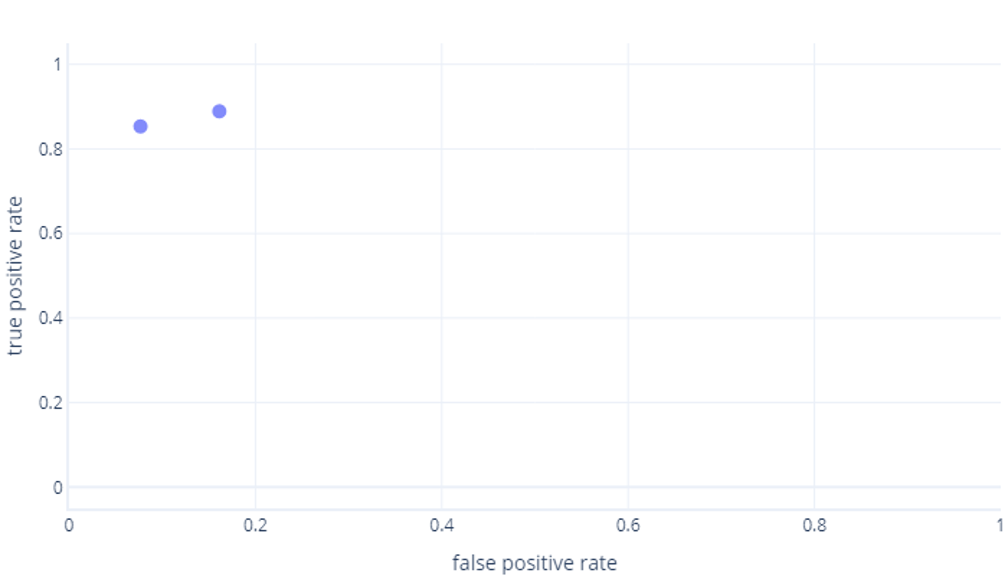
Pokud to uděláme pro prahové hodnoty mezi 0%-100%, můžeme získat graf podobný tomuto:
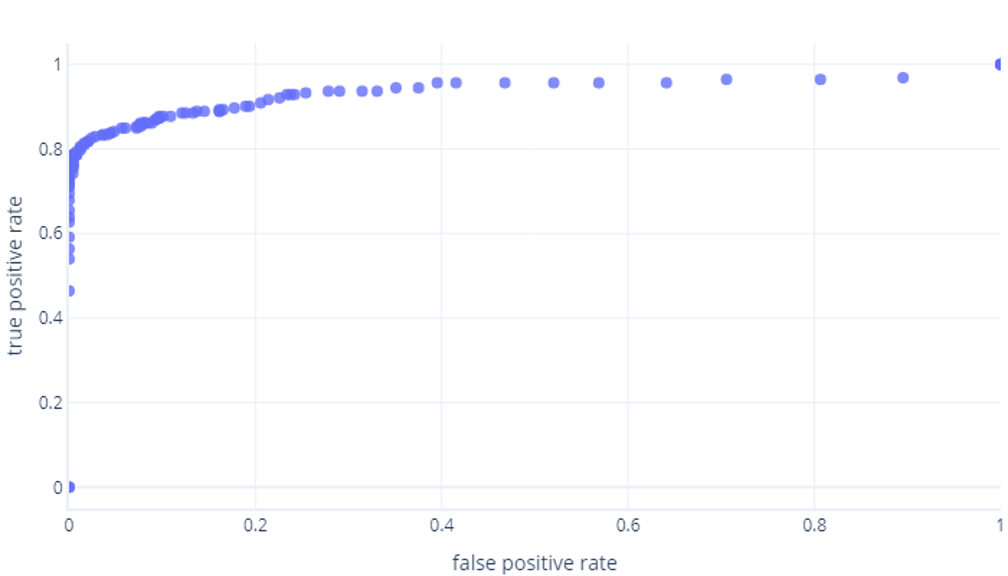
Obvykle se místo toho zobrazuje jako čára:
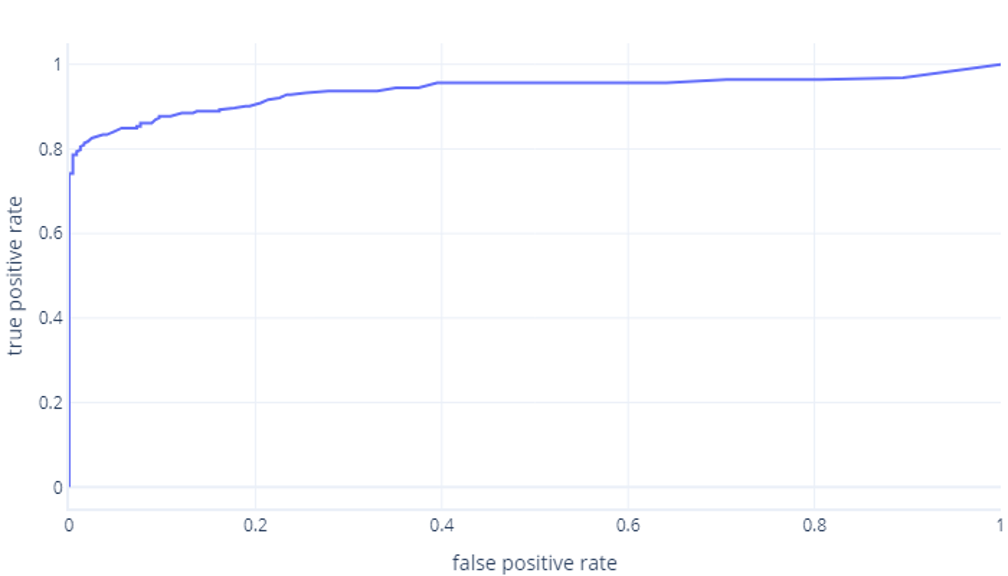
Druhým důvodem, proč tyto grafy můžou být matoucí, je žargon. Mějte na paměti, že chceme vysokou pravdivě pozitivní míru (identifikaci turistických turistů jako takové) a nízkou falešně pozitivní míru (neidentifikovat stromy jako turisté).
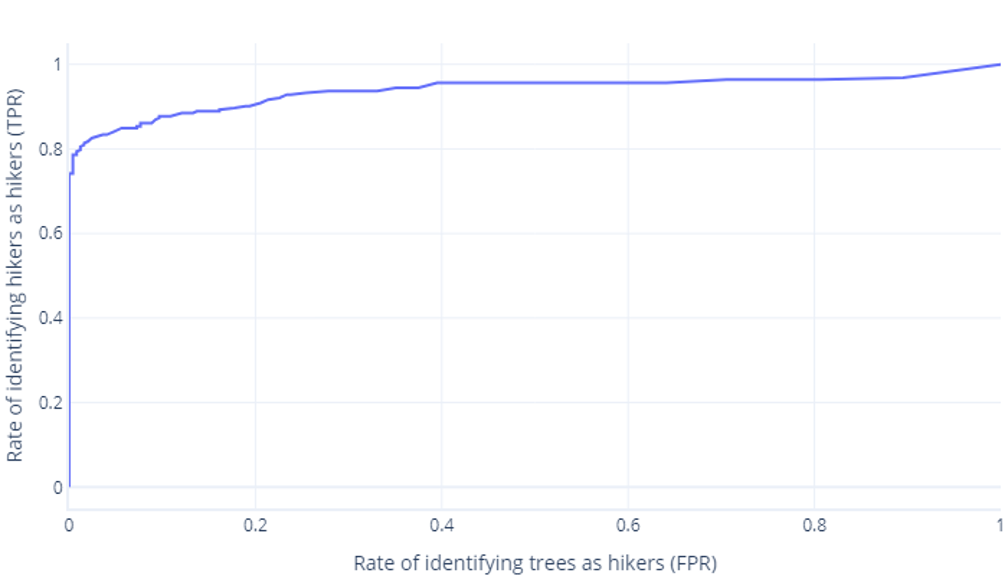
Dobrá ROC, špatná ROC
Pochopení dobrých a špatných křivek ROC je něco nejlepšího udělat v interaktivním prostředí. Až budete připraveni, přejděte k dalšímu cvičení a prozkoumejte toto téma.