Nerovnováhy dat
Když mají popisky dat více kategorií než jinou, říkáme, že máme nerovnováhu dat. Vzpomeňte si například, že v našem scénáři se snažíme identifikovat objekty nalezené senzory dronů. Naše data jsou nevyvážená, protože v našich trénovacích datech existuje výrazně různý počet turistických turistů, zvířat, stromů a kamenů. Můžeme to vidět buď tabulací těchto dat:
| Popisek | Tramp | Zvíře | Strom | Kámen |
|---|---|---|---|---|
| Počet | 400 | 200 | 800 | 800 |
Nebo ho vykreslujete:
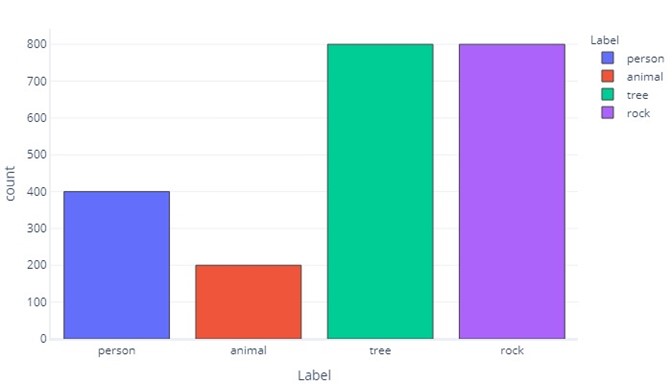
Všimněte si, že většina dat jsou stromy nebo kameny. Tento problém nemá vyvážená datová sada.
Pokud bychom se například snažili předpovědět, jestli je objekt pěší turistikou, zvířetem, stromem nebo kamenem, v ideálním případě bychom chtěli stejný počet všech kategorií, například takto:
| Popisek | Tramp | Zvíře | Strom | Kámen |
|---|---|---|---|---|
| Počet | 550 | 550 | 550 | 550 |
Pokud bychom se jednoduše snažili předpovědět, jestli byl objekt pěší turistikou, ideálně bychom chtěli stejný počet turistických objektů a ne pěších objektů:
| Popisek | Tramp | Non-Hiker |
|---|---|---|
| Počet | 1100 | 1100 |
Proč jsou nevyváženosti dat důležité?
Nevyváženosti dat jsou důležité, protože modely se mohou naučit napodobovat tyto nerovnováhy, pokud není žádoucí. Představte si například, že jsme vytrénovali model logistické regrese, který identifikuje objekty jako pěší turistiku nebo ne pěší turistiku. Pokud dominují trénovací data popisky "hiker", trénování by model předčítá tak, aby téměř vždy vracel popisky "hiker". V reálném světě ale můžeme zjistit, že většina věcí, které drony narazí, jsou stromy. Zkreslený model by pravděpodobně označoval mnoho z těchto stromů jako turisté.
Tento jev probíhá, protože nákladové funkce ve výchozím nastavení určují, jestli byla zadána správná odpověď. To znamená, že pro zkreslenou datovou sadu je nejjednodušší způsob, jak model dosáhnout optimálního výkonu, může být prakticky ignorovat poskytované funkce a vždy nebo téměř vždy vrátit stejnou odpověď. To může mít zničující důsledky. Představte si například, že náš model hiker/not-hiker je trénován na datech, kde jen jeden na 1 000 vzorků obsahuje pěší turistiku. Model, který se naučil vrátit "ne-hiker" pokaždé, má přesnost 99,9 %! Zdá se, že tato statistika je nevyřízená, ale model je nepoužitý, protože nám nikdy neřekne, jestli je někdo na hoře, a my nebudeme vědět, abychom je zachránili, pokud dojde k lavině.
Předsudky v konfuzní matici
Matrice nejasnosti jsou klíčem k identifikaci nerovnováhy dat nebo odchylky modelu. V ideálním scénáři mají testovací data přibližně sudý počet popisků a předpovědi vytvořené modelem jsou také přibližně rozložené mezi popisky. V případě 1000 ukázek může model, který je nestranný, ale často dostává nesprávné odpovědi, vypadat nějak takto:
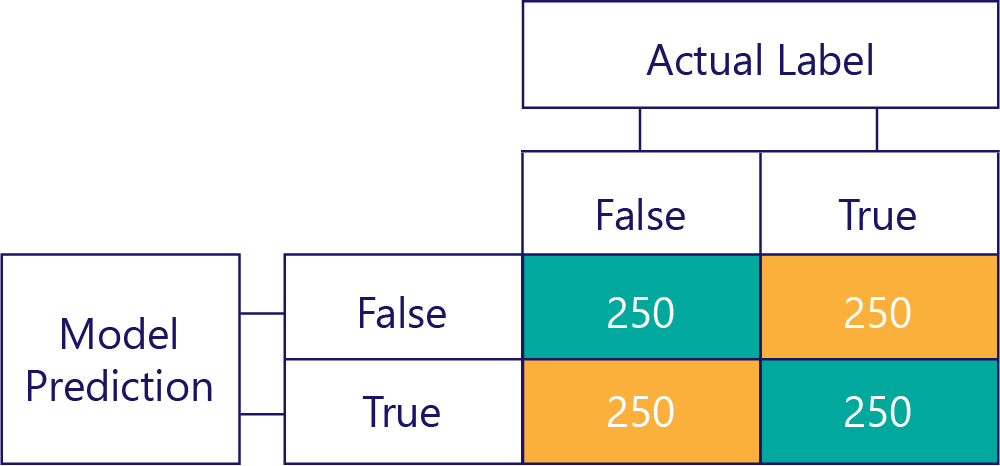
Můžeme říci, že vstupní data jsou nestranná, protože součty řádků jsou stejné (500 každý), což znamená, že polovina popisků je "true" a polovina je "false". Podobně můžeme vidět, že model dává nestranné odpovědi, protože vrací skutečnou polovinu času a nepravdí druhou polovinu času.
Naproti tomu zkreslená data většinou obsahují jeden druh popisku, například takto:
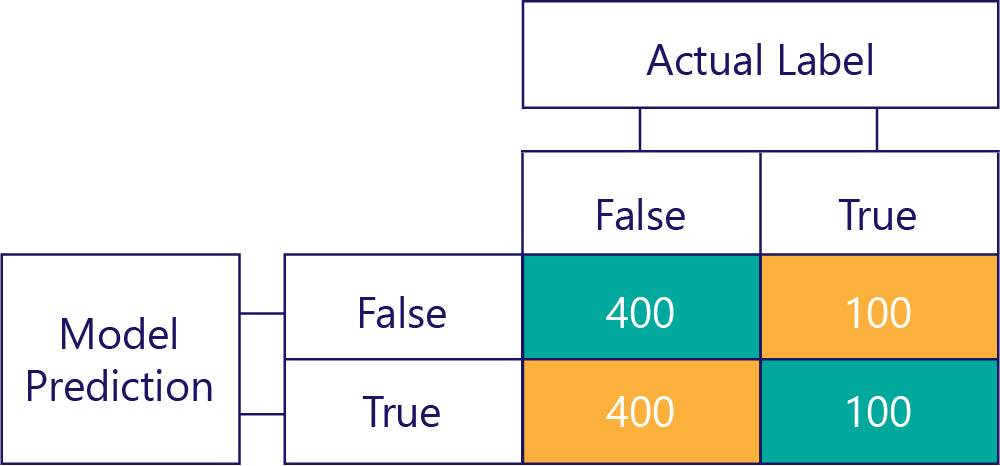
Podobně zkreslený model většinou vytváří jeden druh popisku, například takto:
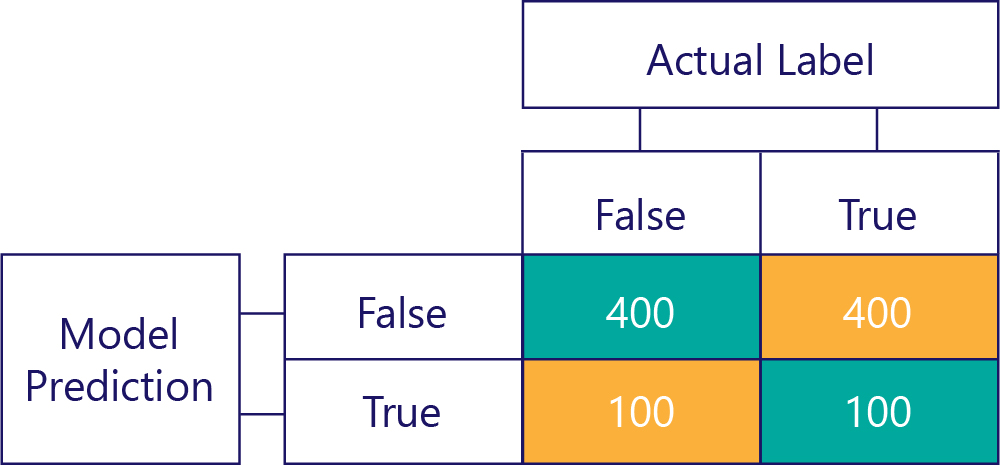
Předsudky modelu nejsou přesné.
Mějte na paměti, že předsudky nejsou přesné. Například některé z předchozích příkladů jsou zkreslené a jiné nejsou, ale všechny ukazují model, který získá správnou odpověď 50 % času. Jako krajnější příklad ukazuje následující matice nestranný model, který je nepřesný:
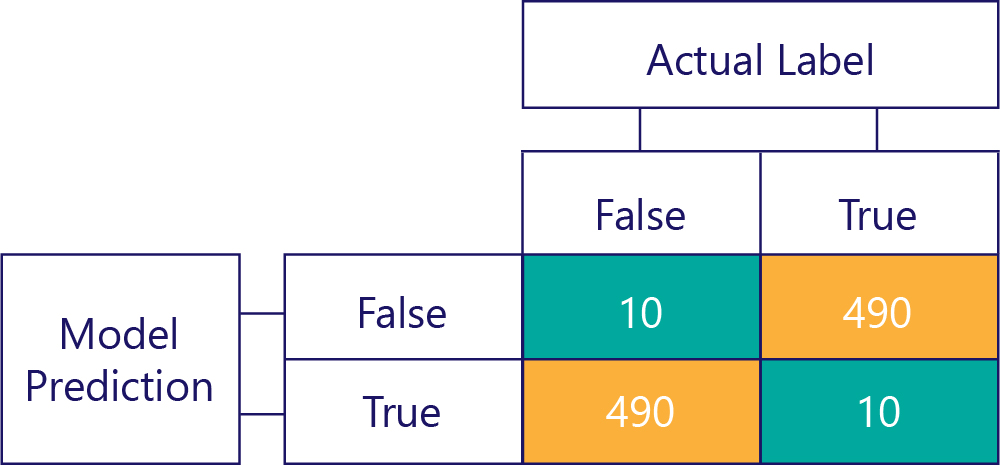
Všimněte si, jak se počet řádků a sloupců přidá do 500, což znamená, že jsou data vyvážená a model není zkreslený. Tento model ale dostává téměř všechny nesprávné odpovědi.
Samozřejmě naším cílem je mít modely přesné a nestranné, například:
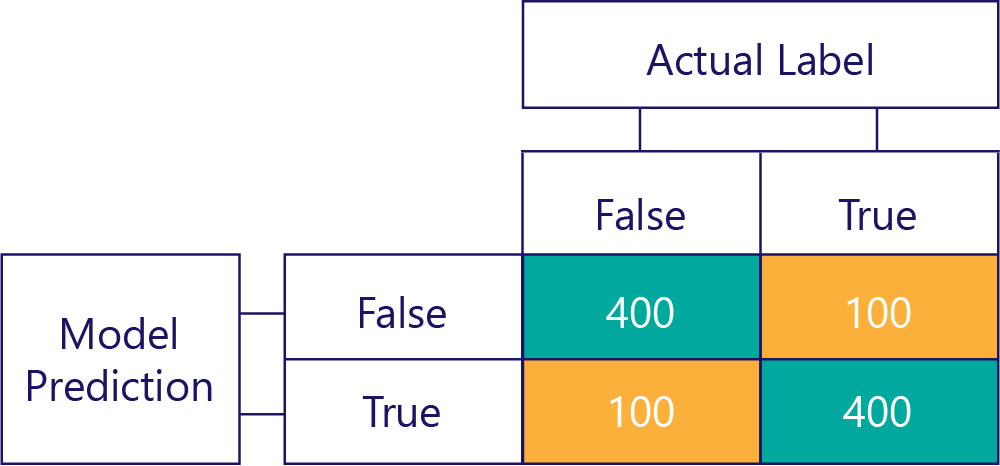
… ale musíme zajistit, aby naše přesné modely nejsou zkreslené, jednoduše proto, že data jsou:
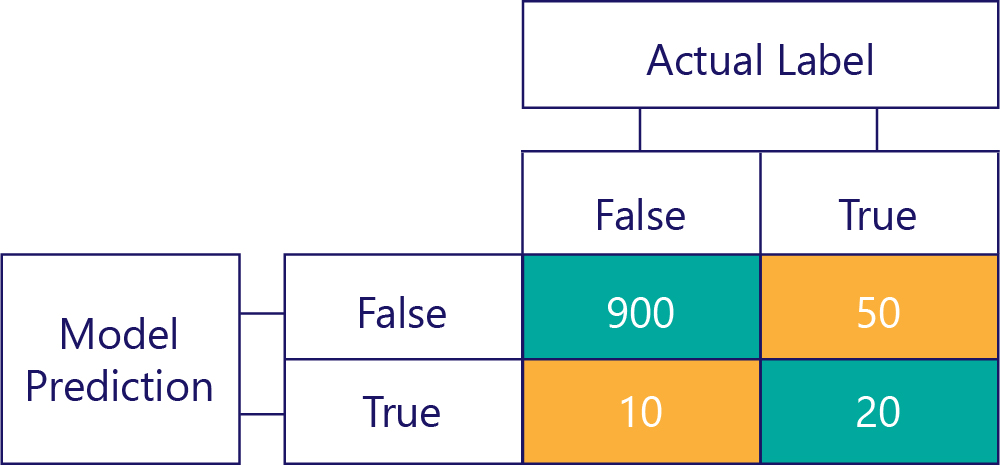
V tomto příkladu si všimněte, že skutečné popisky jsou většinou false (levý sloupec zobrazující nerovnováhu dat) a model také často vrací hodnotu false (horní řádek znázorňující odchylku modelu). Tento model není vhodný pro správné poskytování odpovědí True.
Předcházení důsledkům nevyvážených dat
Mezi nejjednodušší způsoby, jak se vyhnout důsledkům nevyvážených dat, patří:
- Vyhněte se tomu díky lepšímu výběru dat.
- "Převzorkovat" vaše data tak, aby obsahovala duplikáty třídy menšinového označení.
- Proveďte změny nákladové funkce tak, aby upřednostňovala méně běžné popisky. Pokud je například stromově zadána nesprávná odpověď, může funkce nákladů vrátit hodnotu 1; i když se na Hiker provede nesprávná odpověď, může se vrátit 10.
Tyto metody prozkoumáme v následujícím cvičení.