Hloubkové učení

Dokončeno

Hluboké učení je pokročilá forma strojového učení, která se snaží napodobit způsob, jakým se učí lidský mozek. Klíčem k hlubokému učení je vytvoření umělé neurální sítě , která simuluje elektrochemickou aktivitu v biologických neuronech pomocí matematických funkcí, jak je znázorněno tady.

Biologická neurální síť	Umělá neurální síť
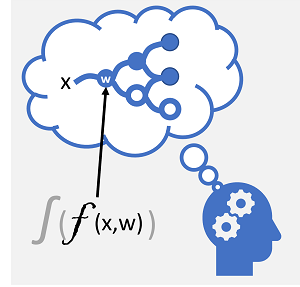
Neurony hoří v reakci na elektrochemické podněty. Při spuštění se signál předává připojeným neuronům.	Každý neuron je funkce, která pracuje se vstupní hodnotou (x) a hmotností (w). Funkce je zabalena do aktivační funkce, která určuje, zda se má výstup předat dál.

Umělé neurální sítě se skládají z několika vrstev neuronů – v podstatě definují hluboko vnořenou funkci. Tato architektura je důvodem, proč se technika označuje jako hluboké učení a modely, které vytváří, se často označují jako hluboké neurální sítě (DNN). Hluboké neurální sítě můžete použít pro mnoho druhů problémů se strojovém učením, včetně regrese a klasifikace, a také specializovanější modely pro zpracování přirozeného jazyka a počítačového zpracování obrazu.

Stejně jako jiné techniky strojového učení probírané v tomto modulu zahrnuje hluboké učení přizpůsobení trénovacích dat funkci, která dokáže předpovědět popisek (y) na základě hodnoty jedné nebo více funkcí (x). Funkce (f(x)) je vnější vrstva vnořené funkce, ve které každá vrstva neurální sítě zapouzdřuje funkce, které pracují s hodnotami x a hmotností (w) s nimi spojenými. Algoritmus použitý k trénování modelu zahrnuje iterativní předávání hodnot funkcí (x) v trénovacích datech přes vrstvy, aby se vypočítaly výstupní hodnoty pro ŷ, ověřují model, aby se vyhodnotily, jak daleko jsou vypočítané hodnoty ŷ od známých hodnot y (které v modelu kvantifikují úroveň chyby nebo ztráty). a pak úpravou hmotnosti (w) snížit ztrátu. Trénovaný model obsahuje konečné hodnoty hmotnosti, které vedou k nejpřesnějším předpovědím.

Příklad – použití hlubokého učení pro klasifikaci

Abychom lépe pochopili, jak funguje model hluboké neurální sítě, pojďme se podívat na příklad, ve kterém se neurální síť používá k definování klasifikačního modelu pro druhy tučňáků.

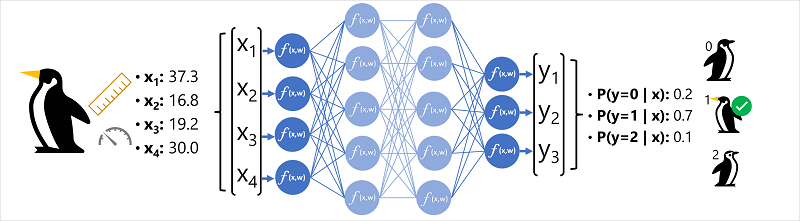
Data funkce (x) se skládají z některých měření tučňáka. Konkrétně se jedná o následující měření:

• Délka účtu tučňáka.
• Hloubka účtu tučňáka.
• Délka tučňákových ploutví.
• Váha tučňáka.

V tomto případě je x vektor čtyř hodnot nebo matematicky x=[x1;x2;x3;x4].

Popisek, který se snažíme předpovědět (y), je druh tučňáka a že existují tři možné druhy, které by to mohly být:

• Adelie
• Gentoo
• Chinstrap

Toto je příklad klasifikačního problému, ve kterém model strojového učení musí předpovědět nejpravděpodobnější třídu, do které pozorování patří. Klasifikační model toho dosahuje predikcí popisku, který se skládá z pravděpodobnosti pro každou třídu. Jinými slovy, y je vektor tří hodnot pravděpodobnosti; jednu pro každou z možných tříd: [P(y=0|x), P(y=1|x), P(y=2|x)].

Proces odvozování predikované třídy tučňáků pomocí této sítě je:

1. Vektor funkce pro pozorování tučňáků je přiváděn do vstupní vrstvy neurální sítě, která se skládá z neuronu pro každou hodnotu x . V tomto příkladu se jako vstup použije následující vektor x : [37.3, 16.8, 19.2, 30.0]
2. Funkce pro první vrstvu neuronů každá vypočítá vážený součet kombinací hodnoty x a hmotnosti w a předá ho aktivační funkci, která určí, jestli splňuje prahovou hodnotu, která se má předat další vrstvě.
3. Každý neuron ve vrstvě je připojen ke všem neuronům v další vrstvě (architektura se někdy označuje jako plně propojená síť), takže výsledky každé vrstvy se předávají přes síť, dokud se nedostanou na výstupní vrstvu.
4. Výstupní vrstva vytváří vektor hodnot; v tomto případě pomocí softmaxu nebo podobné funkce k výpočtu rozdělení pravděpodobnosti pro tři možné třídy tučňáků. V tomto příkladu je výstupní vektor : [0.2, 0.7, 0.1]
5. Prvky vektoru představují pravděpodobnosti pro třídy 0, 1 a 2. Druhá hodnota je nejvyšší, takže model předpovídá, že druh tučňáka je 1 (Gentoo).

Jak se neurální síť učí?

Váhy v neurální síti jsou ústřední pro způsob výpočtu předpovězených hodnot pro popisky. Během procesu trénování se model učí váhy, které povedou k nejpřesnějším předpovědím. Pojďme se podrobněji podívat na proces trénování, abychom pochopili, jak toto učení probíhá.

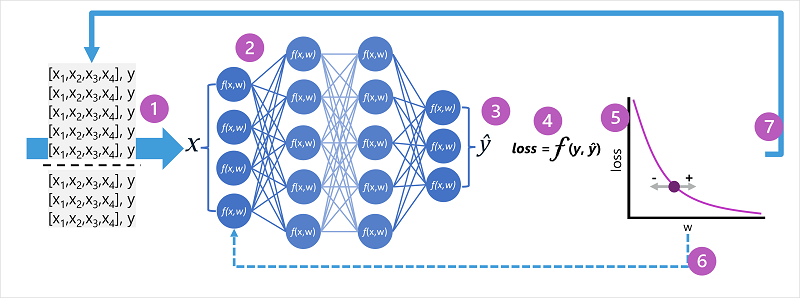
1. Jsou definovány trénovací a ověřovací datové sady a funkce trénování se předávají do vstupní vrstvy.
2. Neurony v každé vrstvě sítě používají svou váhu (které jsou zpočátku přiřazeny náhodně) a předávají data prostřednictvím sítě.
3. Výstupní vrstva vytvoří vektor obsahující počítané hodnoty pro ŷ. Například výstup pro predikci třídy tučňáků může být [0,3. 0.1. 0.6].
4. Funkce ztráty se používá k porovnání predikovaných hodnot ŷ se známými hodnotami y a agregaci rozdílu (což se označuje jako ztráta). Pokud například známá třída pro případ, který vrátil výstup v předchozím kroku , je Chinstrap, pak by hodnota y měla být [0.0, 0.0, 1.0]. Absolutní rozdíl mezi tímto vektorem a vektorem ŷ je [0.3, 0.1; 0.4]. Ve skutečnosti funkce ztráty vypočítá agregovanou odchylku pro více případů a shrnuje ji jako jednu ztrátovou hodnotu.
5. Vzhledem k tomu, že celá síť je v podstatě jedna velká vnořená funkce, může optimalizační funkce pomocí rozdílového počtu vyhodnotit vliv jednotlivých vah v síti na ztrátu a určit, jak by se mohly upravit (nahoru nebo dolů), aby se snížila celková ztráta. Konkrétní technika optimalizace se může lišit, ale obvykle zahrnuje přístup gradientového sestupu , při kterém se každá hmotnost zvyšuje nebo snižuje, aby se minimalizovala ztráta.
6. Změny vah se znovu přemístí do vrstev v síti a nahradí se dříve použité hodnoty.
7. Proces se opakuje během několika iterací ( označovaných jako epochy), dokud nedojde k minimalizaci ztráty a model předpovídá přijatelně přesně.

Poznámka

I když je jednodušší myslet na každý případ v trénovacích datech předávaných sítí jeden po druhém, ve skutečnosti se data rozdělují do matic a zpracovávají se pomocí lineárních algebraických výpočtů. Z tohoto důvodu se trénování neurální sítě nejlépe provádí na počítačích s grafickými procesory (GPU), které jsou optimalizované pro manipulaci s vektory a maticemi.