Regrese
Regresní modely se trénují tak, aby predikovaly hodnoty číselných popisků na základě trénovacích dat, která zahrnují funkce i známé popisky. Proces trénování regresního modelu (nebo jakýkoli model strojového učení pod dohledem) zahrnuje několik iterací, ve kterých použijete odpovídající algoritmus (obvykle s některými parametrizovanými nastaveními) k trénování modelu, vyhodnocení prediktivního výkonu modelu a upřesnění modelu opakováním procesu trénování s různými algoritmy a parametry, dokud nedosáhnete přijatelné úrovně prediktivní přesnosti.
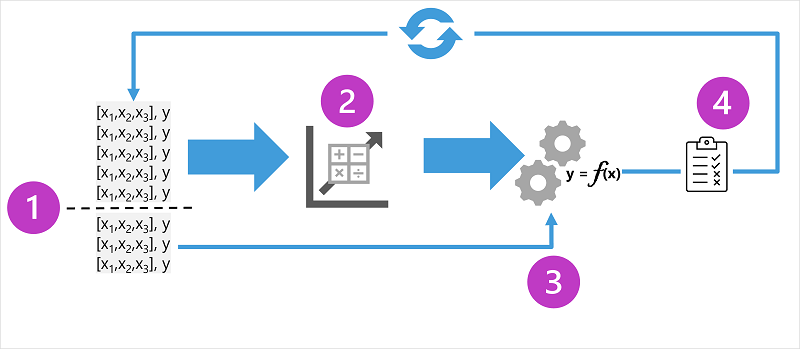
Diagram znázorňuje čtyři klíčové prvky procesu trénování pro modely strojového učení pod dohledem:
- Rozdělte trénovací data (náhodně) a vytvořte datovou sadu, pomocí které se má model vytrénovat a zároveň podmnožinu dat, která použijete k ověření natrénovaného modelu.
- Použijte algoritmus pro přizpůsobení trénovacích dat modelu. V případě regresního modelu použijte regresní algoritmus, jako je lineární regrese.
- Pomocí ověřovacích dat, která jste si podrželi, otestujte model predikcí popisků pro funkce.
- Porovnejte známé skutečné popisky v ověřovací datové sadě s popisky, které model predikoval. Potom agregujte rozdíly mezi predikovanými a skutečnými hodnotami popisků a vypočítejte metriku, která udává, jak přesně model predikoval ověřovací data.
Po každém trénování, ověření a vyhodnocení iterace můžete proces opakovat s různými algoritmy a parametry, dokud nedosáhnete přijatelné metriky vyhodnocení.
Příklad – regrese
Pojďme se podívat na regresi pomocí zjednodušeného příkladu, ve kterém model vytrénujeme, abychom předpověděli číselný popisek (y) na základě jedné hodnoty funkce (x). Většina reálných scénářů zahrnuje více hodnot funkcí, což zvyšuje určitou složitost; ale princip je stejný.
V našem příkladu se budeme držet scénáře prodeje zmrzliny, který jsme probrali dříve. U naší funkce se podíváme na teplotu (předpokládejme, že hodnota je maximální teplota v daném dni) a popisek, který chceme vytrénovat, aby model předpověděl, je počet prodaných zmrzlin v daném dni. Začneme s některými historickými daty, která zahrnují záznamy o denních teplotách (x) a prodeji zmrzliny (y):
 |
 |
|---|---|
| Teplota (x) | Prodej zmrzliny (y) |
| 51 | 0 |
| 52 | 0 |
| 67 | 14 |
| 65 | 14 |
| 70 | 23 |
| 69 | 20 |
| 72 | 23 |
| 75 | 26 |
| 73 | 22 |
| 81 | 30 |
| 78 | 26 |
| 83 | 36 |
Trénování regresního modelu
Začneme rozdělením dat a použitím podmnožina dat k trénování modelu. Tady je trénovací datová sada:
| Teplota (x) | Prodej zmrzliny (y) |
|---|---|
| 51 | 0 |
| 65 | 14 |
| 69 | 20 |
| 72 | 23 |
| 75 | 26 |
| 81 | 30 |
Abychom získali přehled o tom, jak tyto hodnoty x a y mohou vzájemně souviset, můžeme je vykreslit jako souřadnice na dvou osách, například takto:
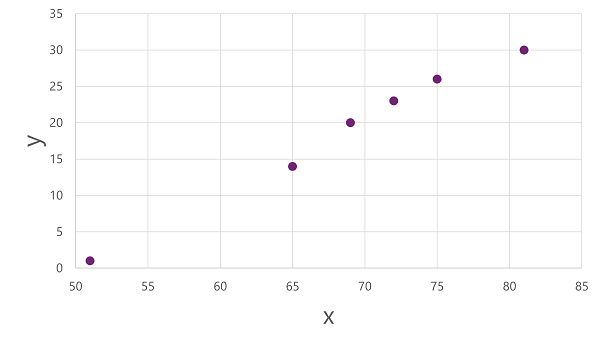
Teď jsme připraveni použít algoritmus na trénovací data a přizpůsobit ho funkci, která použije operaci na x k výpočtu y. Jedním z takových algoritmů je lineární regrese, která funguje odvozením funkce, která vytváří přímku průsečíky hodnot x a y a současně minimalizuje průměrnou vzdálenost mezi přímkou a vykreslovanými body, například takto:
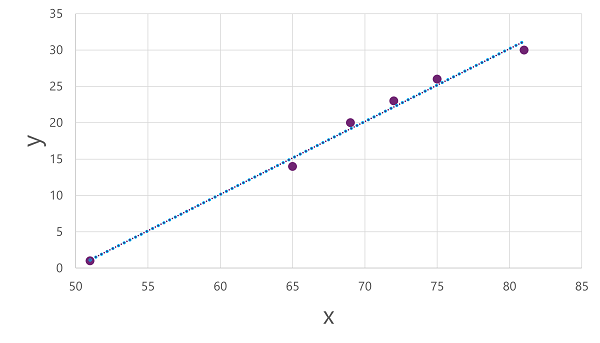
Čára je vizuální reprezentace funkce, ve které sklon přímky popisuje, jak vypočítat hodnotu y pro danou hodnotu x. Čára zachytí osu x na 50, takže když x je 50, y je 0. Jak je vidět ze značek osy v grafu, sklony čáry tak, aby každé zvýšení 5 podél osy x vede ke zvýšení osy 5 nahoru osu y; takže když x je 55, y je 5; když x je 60, y je 10 atd. Pokud chcete vypočítat hodnotu y pro danou hodnotu x, funkce jednoduše odečte 50; jinými slovy, funkce se dá vyjádřit takto:
f(x) = x-50
Pomocí této funkce můžete předpovědět počet zmrzlin prodaných za den s libovolnou teplotou. Předpokládejme například, že předpověď počasí nám říká, že zítra bude 77 stupňů. Náš model můžeme použít k výpočtu 77–50 a předpovědět, že zítra prodáme 27 zmrzlin.
Ale jak přesný je náš model?
Vyhodnocení regresního modelu
Abychom ověřili model a vyhodnotili, jak dobře predikuje, podrželi jsme některá data, pro která známe hodnotu popisku (y). Tady jsou data, která jsme si podrželi:
| Teplota (x) | Prodej zmrzliny (y) |
|---|---|
| 52 | 0 |
| 67 | 14 |
| 70 | 23 |
| 73 | 22 |
| 78 | 26 |
| 83 | 36 |
Pomocí modelu můžeme předpovědět popisek pro každé pozorování v této datové sadě na základě hodnoty funkce (x) a pak porovnat predikovaný popisek (ŷ) se známou skutečnou hodnotou popisku (y).
Použití modelu, který jsme natrénovali dříve, což zapouzdřuje funkci f(x) = x-50, vede k následujícím předpovědím:
| Teplota (x) | Skutečné prodeje (y) | Predikované prodeje (ŷ) |
|---|---|---|
| 52 | 0 | 2 |
| 67 | 14 | 17 |
| 70 | 23 | 20 |
| 73 | 22 | 23 |
| 78 | 26 | 28 |
| 83 | 36 | 33 |
Předpovězené i skutečné popisky můžeme vykreslit s hodnotami funkcí takto:
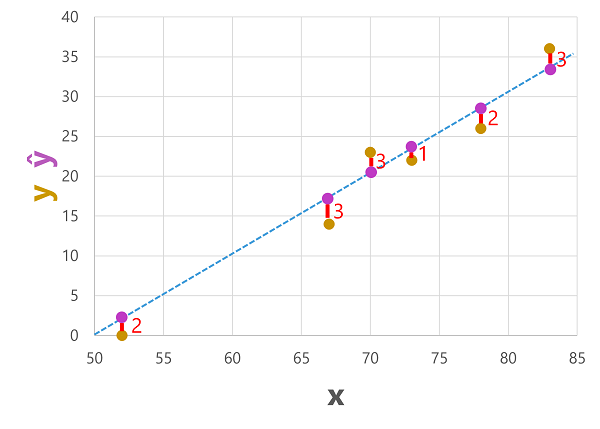
Předpovídané popisky se počítají modelem, takže jsou na spojnici funkce, ale mezi hodnotami ŷ vypočítanými funkcí a skutečnými hodnotami y z ověřovací datové sady, která je na grafu označená jako přímka mezi hodnotami ŷ a y, která ukazuje, jak daleko byla předpověď od skutečné hodnoty.
Metriky vyhodnocení regrese
Na základě rozdílů mezi predikovanými a skutečnými hodnotami můžete vypočítat některé běžné metriky, které se používají k vyhodnocení regresního modelu.
Střední absolutní chyba (MAE)
Rozptyl v tomto příkladu označuje, kolik zmrzlin bylo každé predikce chybné. Nezáleží na tom, jestli byla předpověď přes nebo pod skutečnou hodnotou (například -3 a +3 označují odchylku 3). Tato metrika se označuje jako absolutní chyba pro každou předpověď a lze ji shrnout pro celou sadu ověření jako střední absolutní chybu (MAE).
V příkladu zmrzliny je průměr absolutních chyb (2, 3, 3, 1, 2 a 3) 2,33.
Střední kvadratická chyba (MSE)
Střední absolutní metrika chyb bere v úvahu všechny nesrovnalosti mezi predikovanými a skutečnými popisky. Může však být žádoucí mít model, který je konzistentně chybný o malé množství, než je menší, ale větší chyby. Jedním ze způsobů, jak vytvořit metriku, která "zesiluje" větší chyby rozdělením jednotlivých chyb a výpočtem střední hodnoty kvadratické hodnoty. Tato metrika se označuje jako střední kvadratická chyba (MSE).
V našem příkladu zmrzliny je průměr kvadratický absolutních hodnot (což jsou 4, 9, 9, 1, 4 a 9) 6.
Odmocněná střední kvadratická chyba (RMSE)
Střední kvadratická chyba pomáhá vzít v úvahu velikost chyb, ale protože se rovnají chybovými hodnotami, výsledná metrika už nepředstavuje množství měřené popiskem. Jinými slovy, můžeme říci, že MSE našeho modelu je 6, ale to neměří jeho přesnost z hlediska počtu zmrzlin, které byly špatně diktovány; 6 je jen číselné skóre, které označuje úroveň chyby v predikcích ověřování.
Pokud chceme změřit chybu z hlediska počtu zmrzlin, musíme vypočítat druhou odmocninu MSE, která vytváří metriku nazvanou, nepředpočítaně, odmocnina střední kvadratická chyba. V tomto případě √6, což je 2,45 (zmrzliny).
Koeficient stanovení (R2)
Všechny metriky zatím porovnávají nesrovnalosti mezi predikovanými a skutečnými hodnotami za účelem vyhodnocení modelu. Ve skutečnosti ale existuje nějaký přirozený náhodný rozptyl denního prodeje zmrzliny, který model bere v úvahu. V modelu lineární regrese algoritmus trénování odpovídá přímce, která minimalizuje střední odchylku mezi funkcí a známými hodnotami popisku. Koeficient určení (častěji označovaný jako R2 nebo R-Squared) je metrika, která měří poměr odchylek ve výsledcích ověření, které lze vysvětlit modelem, a ne na některé neobvyklé aspekty ověřovacích dat (například den s velmi neobvyklým počtem zmrzlin z důvodu místního festivalu).
Výpočet pro R2 je složitější než pro předchozí metriky. Porovná součet čtvercových rozdílů mezi predikovanými a skutečnými popisky se součtem čtvercových rozdílů mezi skutečnými hodnotami popisku a střední hodnotou skutečného popisku, například takto:
R2 = 1- ∑(y-ŷ)2 ÷ ∑(y-ȳ)2
Nebojte se příliš mnoho, pokud to vypadá složitě; většina nástrojů strojového učení dokáže vypočítat metriku za vás. Důležitým bodem je, že výsledkem je hodnota mezi 0 a 1, která popisuje poměr odchylek vysvětlených modelem. Jednoduše řečeno, čím blíž k 1 této hodnotě je, tím lépe model zapadá do ověřovacích dat. V případě regresního modelu zmrzliny je hodnota R2 vypočítaná z ověřovacích dat 0,95.
Iterativní trénování
Výše popsané metriky se běžně používají k vyhodnocení regresního modelu. Ve většině reálných scénářů datový vědec použije iterativní proces k opakovanému trénování a vyhodnocení modelu, který se liší:
- Výběr a příprava funkcí (výběr funkcí, které mají být součástí modelu, a výpočty použité na ně, aby se zajistilo lepší přizpůsobení).
- Výběr algoritmu (v předchozím příkladu jsme prozkoumali lineární regresi, ale existuje mnoho dalších regresních algoritmů).
- Parametry algoritmu (číselné nastavení pro řízení chování algoritmu, přesněji označované jako hyperparametry, aby se odlišily od parametrů x a y).
Po několika iteracích je vybraný model, který má za následek nejlepší metriku vyhodnocení, která je pro konkrétní scénář přijatelná.