Cvičení – vytvoření kvantového propletení pomocí Q#

7 min

V předchozí lekci jste se seznámili s konceptem kvantového propletení a stavů Bell.

Teď vytvoříme kvantové propletení pomocí Q# Azure Quantum Development Kit. Pokud chcete vytvořit propletení, musíte použít dvě kvantové operace: operaci Hadamard a operaci Controlled-NOT (CNOT).

Nejprve se podíváme na to, jak tyto operace fungují a jak vytvářejí propletení.

Operace Controlled NOT (CNOT)

Pokud jsou dva qubity propletené, stav jednoho qubitu závisí na stavu druhého qubitu. Proto k propletení dvou qubitů potřebujete operaci, která funguje na obou qubitech současně. Tomu se říká vícequbitová operace.

K vytvoření kvantového propletení potřebujete vícequbitovou CNOT operaci, která je zkratkou controlled-NOT. Tato operace přebírá jako vstup dva qubity, jeden funguje jako řídicí qubit a druhý je target qubit. Operace CNOT překlopí stav druhého qubitu target (qubitu), pokud je stav prvního qubitu (řídicího qubitu) $|1\rangle$.

Vstup	Výstup
$\ket{00}$	$\ket{00}$
$\ket{01}$	$\ket{01}$
$\ket{10}$	$\ket{11}$
$\ket{11}$	$\ket{10}$

V Q#, CNOT operace působí na pole dvou qubitů a překlopí druhý qubit, pokud je Oneprvní qubit .

Propletení s operacemi Hadamard a CNOT

Použitím operace Hadamard, , Hoperace a controlled-NOT, CNOT, můžete transformovat dva qubity ve stavu $|00\rangle$ na stav $\ket{\phiZvon ^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.

Jak to funguje:

Vezměte dva qubity ve stavu $|00\rangle$. Prvním qubitem je řídicí qubit a druhým qubitem target je qubit.
Vytvořte stav superpozice pouze v řídicím qubitu použitím $H$.

$$H |0_c\rangle=\frac{1}{\sqrt{{2}}(|0_c\rangle+|1_c)\rangle$$

Tip

Dolní indexy ${}_c$ a ${}_t$ určují ovládací prvek a target qubity.
Použití operátoru $CNOT$ na řídicí qubit, který je ve stavu superpozice, a target qubit, který je ve stavu $|0_t\rangle$.

$$CNOT \frac{1}{\sqrt{2}}(\ket{0_c+}1_c\ket{)}_t \ket{0} CNOT =2\frac{1}{\sqrt(}0_c 0_t+\ket{1_c 0_t}|\ket{)}=$$$$=\frac{2{1}{\sqrt(CNOT }0_c 0_t\ket{} + CNOT \ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t}+\ket{1_c 1_t)}$$

Vytvořte kvantové propletení v Q#

Začnete vytvořením nového souboru Q# v editoru Visual Studio Code.

Otevřete Visual Studio Code.
Vyberte Soubor > Nový textový soubor a uložte ho jako Main.qs.
Vyberte Zobrazit –> Paleta příkazů a zadejtetarget Azure Quantum QIR. Stiskněte klávesu Enter.
Vyberte Q#: Bez omezení.

Vytvoření stavu $\ket{\phizvonku ^+}$

Začněme vytvořením stavu $\ket{\phizvonku ^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.

Nejprve musíte importovat Microsoft.Quantum.Diagnostics obor názvů z knihovny Standard, která obsahuje DumpMachine funkci. Tato funkce zobrazuje aktuální stav qubitů. Zkopírujte a vložte následující Q# kód do souboru Main.qs .
```
import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
```
Tip

Standardní knihovnu můžete také importovat nahrazením Microsoft.Quantum .Std Například import Std.Diagnostics.* je ekvivalentní s import Microsoft.Quantum.Diagnostics.*.

Main Vytvořte operaci, která vrací dvě Result hodnoty typu, což jsou výsledky měření qubitů.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    // Your code goes here
}

Main Uvnitř operace přidělíte dva qubity q1 a q2, které budou propletené.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());
}

Použijte hadamardovou bránu, Hna první qubit, q1a vložte ji do superpozice stavu. Potom pomocí operace propletete dva qubity CNOT .

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
}

DumpMachine Pomocí funkce zobrazíte aktuální stav qubitů. To není totéž jako měření qubitů.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();
}

Změřte qubity pomocí M operace a uložte výsledky do m1 a m2. Potom pomocí Reset operace resetujte qubity. V Q#systému , musíte vždy resetovat qubity do $|stavu 0\rangle$ .

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {

    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

}

Nakonec vrátí výsledky měření qubitů pomocí return příkazu. Soubor Main.qs by měl vypadat takto:

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

Pokud chcete program spustit na integrovaném simulátoru, klikněte na Spustit nad operací nebo stiskněte Ctrl+F5.Main Výstup se zobrazí v konzole ladění.
Výsledky měření korelují, takže na konci programu získáte výsledek (Zero, Zero) nebo (One, One) se stejnou pravděpodobností.
Diagram okruhu můžete vizualizovat kliknutím na Okruh ze seznamu příkazů nad Main operací. Diagram obvodu znázorňuje bránu Hadamard použitou na první qubit a bránu CNOT použitou na oba qubity.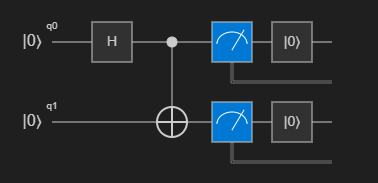

Jak vytvořit další stavy Zvonu

Pokud chcete vytvořit další stavy Bell, musíte pro qubity použít další operace Pauli $X$ a $Z$ .

Pokud například chcete vytvořit stav $\ket{\phiZvonu ^-}=\frac1{\sqrt2}(|00-11\rangle|\rangle),$můžete po použití brány Hadamard použít operaci Pauli $Z$ na řídicí qubit. Operace $Z$ překlopí stav $\ket{+}$ na $\ket{-}$.

Tip

Stavy $\frac{{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ a $\frac{1}{\sqrt{{2}}(|0\rangle -|1\rangle)$ se také označují jako $\ket{+}$ a $\ket{{-}$v uvedeném pořadí.

Jak to funguje:

Vezměte dva qubity ve stavu $|00\rangle$.
Vytvořte stav superpozice pouze v řídicím qubitu použitím $H$.

$$H |0_c\rangle=\frac{{1}{\sqrt{2}}(|0_c\rangle+|1_c\rangle) =\ket{+_c}$$
$Použití operace Z$ na řídicí qubit.

$$Z \frac{{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)=\frac{1}{\sqrt{{2}}(|0_c-1_c\rangle|\rangle)_c=\ket{{-}$$
Použití operátoru $CNOT$ na řídicí qubit a target qubit, který je ve stavu $|0_t\rangle$.

$$CNOT \frac{1}{\sqrt{2}}(\ket{0_c-1_c}\ket{)}_t \ket{0} CNOT =2\frac{1}{\sqrt(}0_c 0_t-1_c 0_t\ket{}|\ket{)}=$$$$=\frac{2{1}{\sqrt(CNOT }0_c 0_t\ket{} - CNOT \ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t-1_c 1_t)}\ket{}$$

Podobně lze bellové stavy $\ket{\psi^+}$ a $\ket{\psi^-}$ vytvořit použitím operací Pauli $X$ a $Z$ na qubity.

Stav $\ket{\psizvonu ^+}=\frac1{\sqrt2}(|01\rangle+|10\rangle)$ lze vytvořit použitím operace Pauli $X$ na target qubit po použití brány Hadamard.
Stav $\ket{\psiZvonu ^-}=\frac1{\sqrt2}(|01-10\rangle|\rangle)$ lze vytvořit použitím Pauli $Z$ na řídicí qubit a Pauli $X$ na target qubit po použití brány Hadamard.

Vytvoření stavu $\ket{\phizvonku ^-}$ in Q#

Q# Upravte kód tak, aby vytvořil stav $\ket{\phizvonku ^-}$. Soubor Main.qs by měl vypadat takto:

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    Z(q1); // Apply the Pauli Z operation to the control qubit
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

Pokud chcete program spustit na integrovaném simulátoru, klikněte na Spustit nad operací nebo stiskněte Ctrl+F5.Main Výstup se zobrazí v konzole ladění.
Diagram okruhu můžete vizualizovat kliknutím na Okruh ze seznamu příkazů nad Main operací. Diagram obvodu znázorňuje bránu Hadamard použitou na první qubit, bránu Pauli $Z$ použitou na první qubit a bránu CNOT použitou na oba qubity.

V další lekci se dozvíte, jak používat propletení k odesílání kvantových informací, procesu označovaného jako kvantové teleportace.