Použití pokročilých technik zkoumání dat

  • 7 min

Pokročilé techniky zkoumání dat, jako je analýza korelace a redukce dimenzí, pomáhají odhalit skryté vzory a vztahy v datech a poskytují cenné přehledy, které mohou vést k rozhodování.

Korelace

Korelace je statistická metoda použitá k vyhodnocení síly a směru lineárního vztahu mezi dvěma kvantitativními proměnnými. Korelační koeficient se pohybuje od -1 do 1.

Korelační koeficient Popis
1 Označuje dokonalou pozitivní lineární korelaci. S nárůstem jedné proměnné se zvyšuje i druhá proměnná.
-1 Označuje dokonalou negativní lineární korelaci. S nárůstem jedné proměnné se druhá proměnná sníží.
0 Označuje žádnou lineární korelaci. Obě proměnné nemají vztah mezi sebou.

Pojďme pomocí datové sady tučňáků vysvětlit, jak korelace funguje.

Poznámka:

Použitá datová sada tučňáků je podmnožinou dat shromážděných a zpřístupněných dr. KristenEm Gormanem a stanicí Palmer, Antarktida LTER, členem dlouhodobé ekologické výzkumné sítě.

import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd

# Load the penguins dataset
penguins = pd.read_csv('https://raw.githubusercontent.com/MicrosoftLearning/dp-data/main/penguins.csv')

# Calculate the correlation matrix
corr = penguins.corr()

# Create a heatmap
sns.heatmap(corr, annot=True)
plt.show()

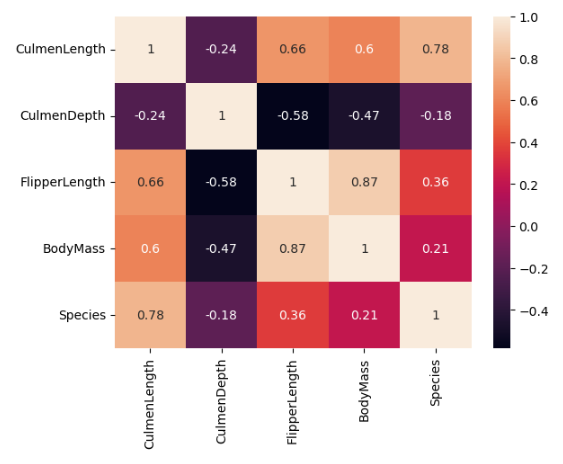
Screenshot of the correlation using heat maps in a notebook.

Nejsilnější korelace v datové sadě je mezi FlipperLength proměnnými a BodyMass s korelačním koeficientem 0,87. To naznačuje, že tučňáky s většími flippery mají tendenci mít větší tělo hmotnost.

Identifikace a analýza korelací jsou důležité z následujících důvodů.

  • Prediktivní analýza: Pokud jsou dvě proměnné vysoce korelované, můžeme předpovědět jednu proměnnou z druhé.
  • Výběr funkce: Pokud jsou dvě funkce vysoce korelované, můžeme jednu odstranit, protože neposkytuje jedinečné informace.
  • Principy relací: Korelace pomáhá pochopit vztah mezi různými proměnnými v datech.

Důležité

V zásadě korelace neznamená příčinnou souvislost. Jen proto, že dvě proměnné korelují, neznamená, že změny v jedné proměnné způsobují změny v druhé.

Analýza hlavních komponent (PCA)

Analýzu hlavních komponent (PCA) je možné použít ke zkoumání i předběžnému zpracování dat.

V mnoha scénářích reálných dat se zabýváme vysoce dimenzionálními daty, se kterými se dá těžko pracovat. Při zkoumání pomáhá ANALÝZA PCA snížit počet proměnných při zachování většiny původních informací. To usnadňuje práci s daty a méně náročnými na prostředky pro algoritmy strojového učení.

Pro zjednodušení příkladu pracujeme s datovou sadou tučňáků, která obsahuje pouze pět proměnných. Při práci s větší datovou sadou byste ale postup postupoval podobně.

import pandas as pd
import seaborn as sns
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# Load the penguins dataset
penguins = pd.read_csv('https://raw.githubusercontent.com/MicrosoftLearning/dp-data/main/penguins.csv')

# Remove missing values
penguins = penguins.dropna()

# Prepare the data and target
X = penguins.drop('Species', axis=1)
y = penguins['Species']

# Initialize and apply PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

# Plot the data
plt.figure(figsize=(8, 6))
for color, target in zip(['navy', 'turquoise', 'darkorange'], penguins['Species'].unique()):
    plt.scatter(X_pca[y == target, 0], X_pca[y == target, 1], color=color, alpha=.8, lw=2,
                label=target)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('PCA of Penguins dataset')
plt.show()

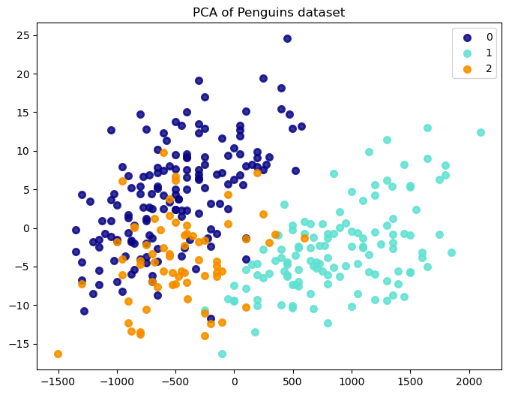
Screenshot of how to apply the principal component analysis to reduce the dimensionality, and then plot the data points in a scatter plot.

Použitím PCA v datové sadě tučňáků můžeme těchto pět proměnných snížit na dvě hlavní komponenty, které zachycují největší odchylku v datech. Tato transformace snižuje rozměry dat z pěti dimenzí na dvě. Pak můžeme vytvořit 2D bodový graf, který vizualizuje data a identifikuje shluky tučňáků s podobnými charakteristikami.

Každý bod v grafu představuje tučňáka z datové sady. Hodnoty první a druhé hlavní komponenty (x a y) určují pozici bodu.

Jedná se o nové proměnné, které PCA vytváří z lineárních kombinací CulmenLength, CulmenDepth, FlipperLength, BodyMassa Species proměnných. První hlavní komponenta zachycuje největší odchylku v datech a každá další komponenta zachycuje menší odchylku.

Výsledky ukazují oddělení mezi tučňáky různých druhů. To znamená, že body stejné barvy (druhů) jsou blíže a body různých barev jsou dále od sebe. Rozdíly v rozdělení funkcí pro různé třídy vedou k tomuto oddělení, což naznačuje, že tyto druhy můžeme odlišit na základě jejich atributů.