Lomené čáry a parametrické rovnice

Pomocí SkiaSharpu můžete vykreslit libovolnou čáru, kterou můžete definovat pomocí parametrických rovnic.

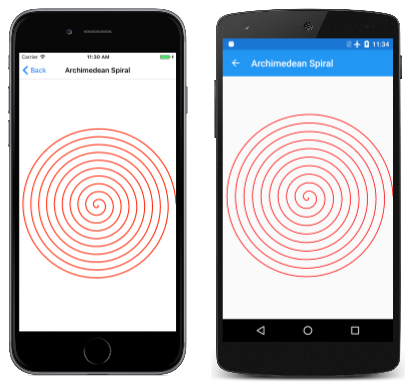
V části Křivky a cesty SkiaSharp v této příručce uvidíte různé metody, které SKPath definují vykreslení určitých typů křivek. Někdy je však nutné nakreslit typ křivky, který není přímo podporován SKPath. V takovém případě můžete pomocí čáry (kolekce propojených čar) nakreslit libovolnou křivku, kterou můžete matematicky definovat. Pokud nastavíte, aby řádky byly dostatečně malé a dostatečně velké, výsledek bude vypadat jako křivka. Tato spirála je ve skutečnosti 3 600 malých čar:

Obecně je nejlepší definovat křivku z hlediska dvojice parametrických rovnic. Jedná se o rovnice souřadnic X a Y, které jsou závislé na třetí proměnné, někdy volané t pro čas. Například následující parametrické rovnice definují kruh s poloměrem 1 na střed v bodě (0, 0) pro t od 0 do 1:

x = cos(2πt)

y = sin(2πt)

Pokud chcete poloměr větší než 1, můžete jednoduše vynásobit sinusové a kosinusové hodnoty tímto poloměrem a pokud potřebujete přesunout střed do jiného umístění, přidejte tyto hodnoty:

x = xCenter + radius·cos(2πt)

y = yCenter + radius·sin(2πt)

U tří teček se osami paralelními k vodorovné a svislé ose jsou zapojeny dvě paprsky:

x = xCenter + xRadius·cos(2πt)

y = yCenter + yRadius·sin(2πt)

Potom můžete ekvivalentní kód SkiaSharp umístit do smyčky, která vypočítá různé body a přidá je do cesty. Následující kód SkiaSharp vytvoří SKPath objekt pro tři tečky, které vyplní plochu zobrazení. Smyčka prochází 360 stupňů přímo. Střed je polovina šířky a výšky povrchu displeje, a proto jsou dvě paprsky:

SKPath path = new SKPath();

for (float angle = 0; angle < 360; angle += 1)
{
    double radians = Math.PI * angle / 180;
    float x = info.Width / 2 + (info.Width / 2) * (float)Math.Cos(radians);
    float y = info.Height / 2 + (info.Height / 2) * (float)Math.Sin(radians);

    if (angle == 0)
    {
        path.MoveTo(x, y);
    }
    else
    {
        path.LineTo(x, y);
    }
}
path.Close();

Výsledkem je tři tečky definované 360 malými čárami. Při vykreslení se zobrazí hladce.

Samozřejmě nemusíte vytvářet tři tečky pomocí čáry, protože SKPath obsahuje metodu AddOval , která ji udělá za vás. Můžete ale chtít nakreslit vizuální objekt, který není poskytován SKPath.

Archimedean Spirála stránka má kód, který se podobá elipse kódu, ale s zásadním rozdílem. Smyčka se pohybuje kolem 360 stupňů kruhu 10krát a nepřetržitě upravuje poloměr:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
    float radius = Math.Min(center.X, center.Y);

    using (SKPath path = new SKPath())
    {
        for (float angle = 0; angle < 3600; angle += 1)
        {
            float scaledRadius = radius * angle / 3600;
            double radians = Math.PI * angle / 180;
            float x = center.X + scaledRadius * (float)Math.Cos(radians);
            float y = center.Y + scaledRadius * (float)Math.Sin(radians);
            SKPoint point = new SKPoint(x, y);

            if (angle == 0)
            {
                path.MoveTo(point);
            }
            else
            {
                path.LineTo(point);
            }
        }

        SKPaint paint = new SKPaint
        {
            Style = SKPaintStyle.Stroke,
            Color = SKColors.Red,
            StrokeWidth = 5
        };

        canvas.DrawPath(path, paint);
    }
}

Výsledek se také nazývá aritmetická spirála , protože posun mezi jednotlivými smyčkami je konstantní:

Všimněte si, že se SKPath vytvoří v using bloku. To SKPath spotřebovává více paměti než SKPath objekty v předchozích programech, což naznačuje, že using blok je vhodnější k odstranění jakýchkoli nespravovaných prostředků.

Související odkazy

• Rozhraní API SkiaSharp