series_fit_poly()
Platí pro: ✅Microsoft Fabric✅Azure Data Explorer✅Azure Monitor✅Microsoft Sentinel
Použije polynomovou regresi z nezávislé proměnné (x_series) na závislá proměnnou (y_series). Tato funkce přebírá tabulku obsahující více řad (dynamická číselná pole) a vygeneruje nejvhodnější polynomický polynom pro každou řadu pomocí polynomické regrese.
Tip
- Pro lineární regresi rovnoměrně rozložené řady vytvořené operátorem make-series použijte jednodušší funkci series_fit_line(). Viz příklad 2.
- Pokud je x_series dodán a regrese se provádí pro vysoký stupeň, zvažte normalizaci rozsahu [0–1]. Viz příklad 3.
- Pokud je x_series typu datetime, musí být převeden na dvojité a normalizované. Viz příklad 3.
- Referenční implementaci polynomické regrese pomocí vloženého Pythonu najdete v tématu series_fit_poly_fl().
Syntaxe
T | extend series_fit_poly( y_series [ , x_series , stupeň ])
Přečtěte si další informace o konvencích syntaxe.
Parametry
| Název | Type | Požadováno | Popis |
|---|---|---|---|
| y_series | dynamic |
✔️ | Matice číselných hodnot obsahující závislých proměnných. |
| x_series | dynamic |
Matice číselných hodnot obsahující nezávislou proměnnou. Vyžaduje se pouze pro nerovnoměrně rozmístěné řady. Pokud není zadaný, nastaví se na výchozí hodnotu [1, 2, ..., length(y_series)]. | |
| stupeň | Požadované pořadí polynomu pro přizpůsobení. Například 1 pro lineární regresi, 2 pro kvadratickou regresi atd. Výchozí hodnota je 1, což označuje lineární regresi. |
Návraty
Funkce series_fit_poly() vrátí následující sloupce:
rsquare: r-square je standardní míra kvality fit. Hodnota je číslo v rozsahu [0–1], kde 1 – je to nejlepší možné přizpůsobení a 0 znamená, že data nejsou seřazená a nevejdou se do žádné čáry.coefficients: Číselná matice držící koeficienty nejlépe fitované polynomu s daným stupněm seřazeným od nejvyššího koeficientu výkonu k nejnižšímu.variance: Rozptyl závislé proměnné (y_series).rvariance: Reziduální rozptyl, který je rozptylem mezi hodnotami vstupních dat, přibližnými hodnotami.poly_fit: Číselná matice obsahující řadu hodnot nejlépe fitovaných polynomů. Délka řady se rovná délce závislé proměnné (y_series). Hodnota se používá pro grafy.
Příklady
Příklad 1
Polynom pátého řádu s šumem na osách x &y:
range x from 1 to 200 step 1
| project x = rand()*5 - 2.3
| extend y = pow(x, 5)-8*pow(x, 3)+10*x+6
| extend y = y + (rand() - 0.5)*0.5*y
| summarize x=make_list(x), y=make_list(y)
| extend series_fit_poly(y, x, 5)
| project-rename fy=series_fit_poly_y_poly_fit, coeff=series_fit_poly_y_coefficients
|fork (project x, y, fy) (project-away x, y, fy)
| render linechart
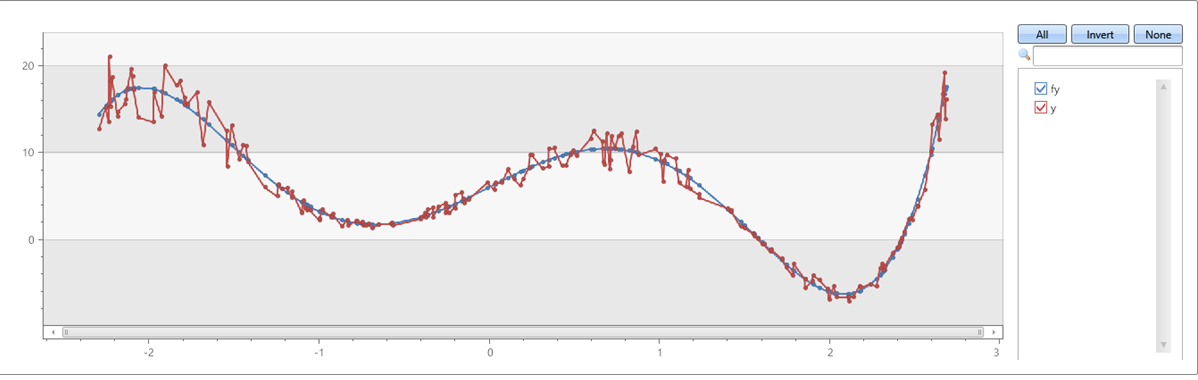
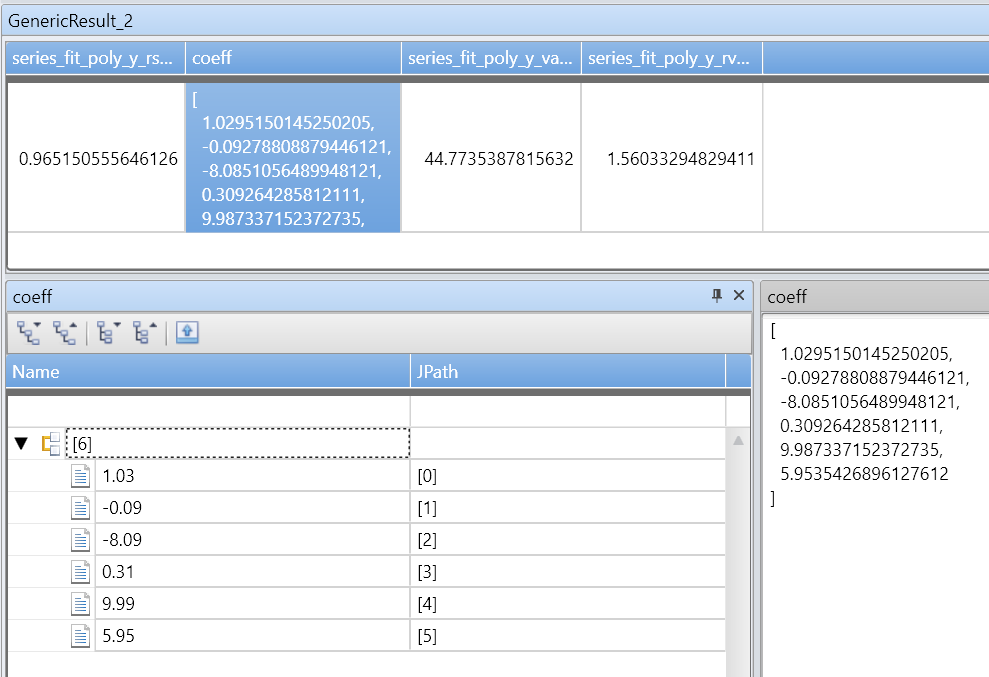
Příklad 2
Ověřte, že series_fit_poly hodnota degree=1 odpovídá series_fit_line:
demo_series1
| extend series_fit_line(y)
| extend series_fit_poly(y)
| project-rename y_line = series_fit_line_y_line_fit, y_poly = series_fit_poly_y_poly_fit
| fork (project x, y, y_line, y_poly) (project-away id, x, y, y_line, y_poly)
| render linechart with(xcolumn=x, ycolumns=y, y_line, y_poly)
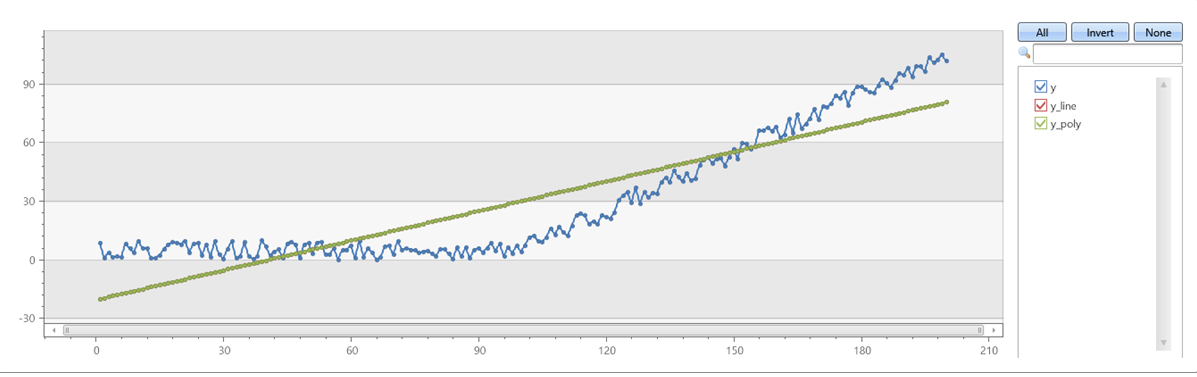

Příklad 3
Nepravidelná (nerovnoměrně rozložená) časová řada:
//
// x-axis must be normalized to the range [0-1] if either degree is relatively big (>= 5) or original x range is big.
// so if x is a time axis it must be normalized as conversion of timestamp to long generate huge numbers (number of 100 nano-sec ticks from 1/1/1970)
//
// Normalization: x_norm = (x - min(x))/(max(x) - min(x))
//
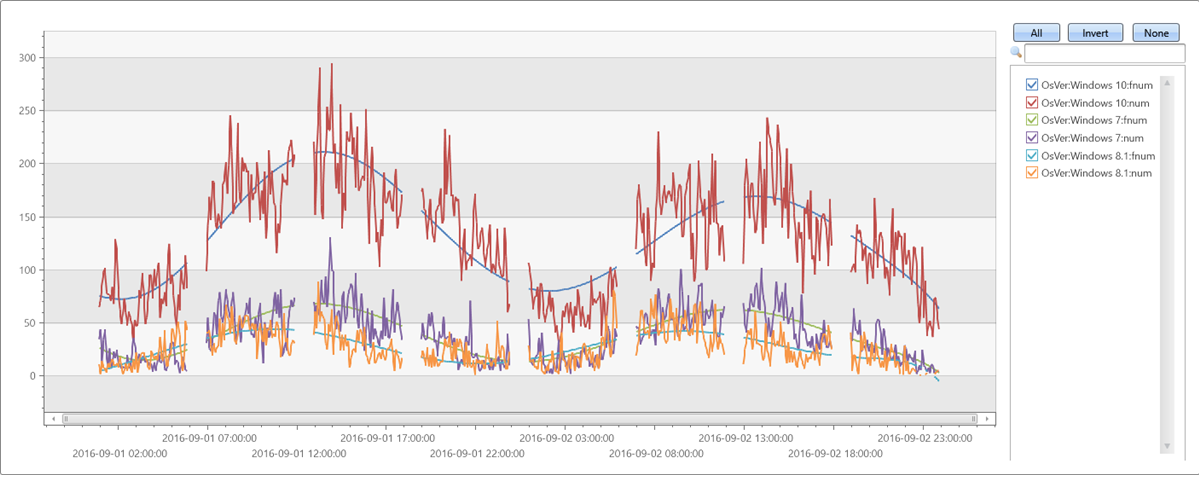
irregular_ts
| extend series_stats(series_add(TimeStamp, 0)) // extract min/max of time axis as doubles
| extend x = series_divide(series_subtract(TimeStamp, series_stats__min), series_stats__max-series_stats__min) // normalize time axis to [0-1] range
| extend series_fit_poly(num, x, 8)
| project-rename fnum=series_fit_poly_num_poly_fit
| render timechart with(ycolumns=num, fnum)