hll_merge()

Platí pro: ✅Microsoft Fabric✅Azure Data Explorer✅Azure Monitor✅Microsoft Sentinel

Sloučí výsledky HLL. Toto je skalární verze agregační verze hll_merge().

Přečtěte si o základním algoritmu (HyperLogLog) a o přesnosti odhadu.

Důležité

Výsledky hll(), hll_if() a hll_merge() je možné uložit a později načíst. Můžete například chtít vytvořit denní souhrn jedinečných uživatelů, který se pak dá použít k výpočtu týdenních počtů. Přesné binární znázornění těchto výsledků se však může v průběhu času změnit. Neexistuje žádná záruka, že tyto funkce budou mít identické výsledky pro stejné vstupy, a proto nedoporučujeme spoléhat se na ně.

Syntaxe

hll_merge(hll, hll2, [ hll3, ... ])

Přečtěte si další informace o konvencích syntaxe.

Parametry

Název	Type	Požadováno	Popis
hll, hll2, ...	string	✔️	Názvy sloupců obsahující hodnoty HLL, které chcete sloučit. Funkce očekává mezi 2 až 64 argumenty.

Návraty

Vrátí jednu hodnotu HLL. Hodnota je výsledkem sloučení sloupců hll, hll2, ... HllN.

Příklady

Tento příklad ukazuje hodnotu sloučených sloupců.

Spuštění dotazu

range x from 1 to 10 step 1 
| extend y = x + 10
| summarize hll_x = hll(x), hll_y = hll(y)
| project merged = hll_merge(hll_x, hll_y)
| project dcount_hll(merged)

Výstup

dcount_hll_merged
20

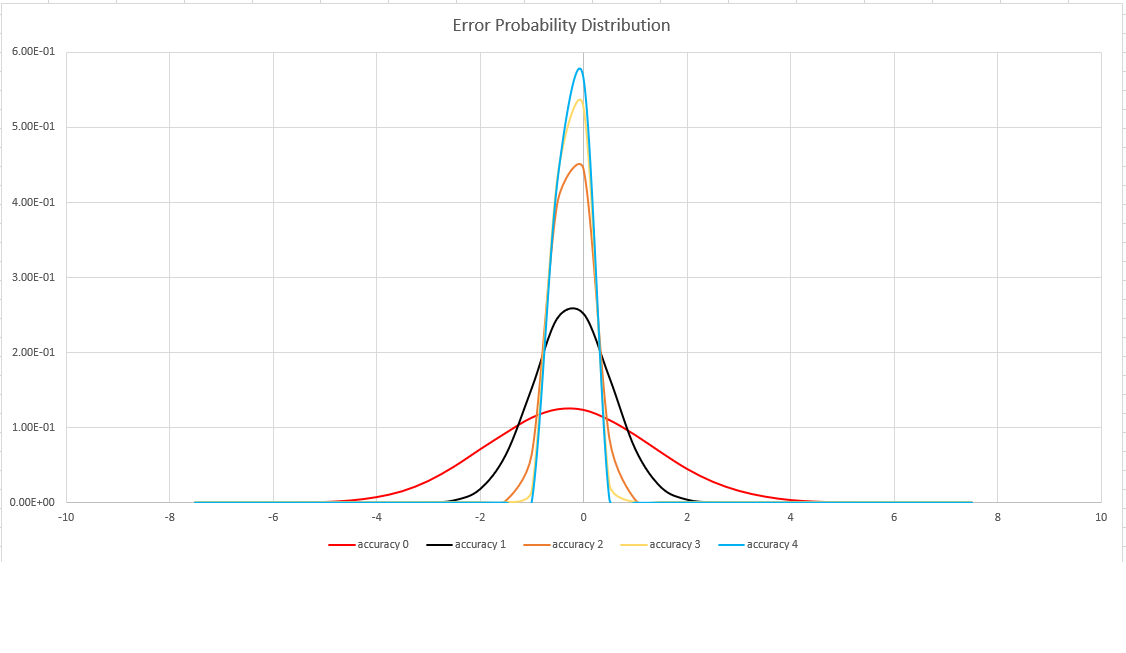
Přesnost odhadu

Tato funkce používá variantu algoritmu HyperLogLog (HLL), který provede stochastický odhad kardinality sady. Algoritmus poskytuje "knoflík", který lze použít k vyvážení přesnosti a doby provádění na velikost paměti:

Přesnost	Chyba (%)	Počet položek
0	1.6	212
0	0,8	214
2	0,4	216
3	0,28	217
4	0,2	218

Poznámka:

Sloupec "entry count" je počet čítačů 1 bajtů v implementaci HLL.

Algoritmus obsahuje některá ustanovení pro dosažení dokonalého počtu (nula chyb), pokud je nastavená kardinalita dostatečně malá:

• Pokud je 1úroveň přesnosti , vrátí se 1 000 hodnot.
• Pokud je 2úroveň přesnosti , vrátí se 8 000 hodnot.

Svázaná chyba je pravděpodobnostní, nikoli teoretická mez. Hodnota je směrodatná odchylka rozdělení chyb (sigma) a 99,7 % odhadů bude mít relativní chybu pod 3 x sigma.

Následující obrázek znázorňuje funkci rozdělení pravděpodobnosti relativní chyby odhadu v procentech pro všechna podporovaná nastavení přesnosti: