Různé způsoby spuštění nástroje pro odhad prostředků
V tomto článku se naučíte pracovat s nástrojem pro odhad prostředků Azure Quantum. Estimátor prostředků vám pomůže odhadnout prostředky potřebné ke spuštění kvantového programu na kvantovém počítači. Pomocí Nástroje pro odhad prostředků můžete odhadnout počet qubitů, počet bran a hloubku okruhu potřebného ke spuštění kvantového programu.
Nástroj pro odhad prostředků je k dispozici v editoru Visual Studio Code s rozšířením Quantum Development Kit. Další informace najdete v tématu Instalace sady Quantum Development Kit.
Varování
Estimátor prostředků na webu Azure Portal je zastaralý. Doporučujeme přejít na místní estimátor prostředků v editoru Visual Studio Code, který je součástí sady Quantum Development Kit.
Požadavky pro VS Code
- Nejnovější verze editoru Visual Studio Code nebo otevření editoru VS Code na webu
- Nejnovější verze rozšíření Quantum Development Kit. Podrobnosti o instalaci najdete v tématu Nastavení rozšíření QDK.
Tip
Ke spuštění nástroje pro odhad prostředků nemusíte mít účet Azure.
Vytvoření nového souboru Q#
- Otevřete Visual Studio Code a výběrem možnosti Soubor > nový textový soubor vytvořte nový soubor.
- Uložte soubor jako
ShorRE.qs. Tento soubor bude obsahovat kód Q# pro váš program.
Vytvoření kvantového algoritmu
Zkopírujte do ShorRE.qs souboru následující kód:
import Std.Arrays.*;
import Std.Canon.*;
import Std.Convert.*;
import Std.Diagnostics.*;
import Std.Math.*;
import Std.Measurement.*;
import Microsoft.Quantum.Unstable.Arithmetic.*;
import Std.ResourceEstimation.*;
operation Main() : Unit {
let bitsize = 31;
// When choosing parameters for `EstimateFrequency`, make sure that
// generator and modules are not co-prime
let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
}
// In this sample we concentrate on costing the `EstimateFrequency`
// operation, which is the core quantum operation in Shors algorithm, and
// we omit the classical pre- and post-processing.
/// # Summary
/// Estimates the frequency of a generator
/// in the residue ring Z mod `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order (period)
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## bitsize
/// Number of bits needed to represent the modulus.
///
/// # Output
/// The numerator k of dyadic fraction k/2^bitsPrecision
/// approximating s/r.
operation EstimateFrequency(
generator : Int,
modulus : Int,
bitsize : Int
)
: Int {
mutable frequencyEstimate = 0;
let bitsPrecision = 2 * bitsize + 1;
// Allocate qubits for the superposition of eigenstates of
// the oracle that is used in period finding.
use eigenstateRegister = Qubit[bitsize];
// Initialize eigenstateRegister to 1, which is a superposition of
// the eigenstates we are estimating the phases of.
// We first interpret the register as encoding an unsigned integer
// in little endian encoding.
ApplyXorInPlace(1, eigenstateRegister);
let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);
// Use phase estimation with a semiclassical Fourier transform to
// estimate the frequency.
use c = Qubit();
for idx in bitsPrecision - 1..-1..0 {
within {
H(c);
} apply {
// `BeginEstimateCaching` and `EndEstimateCaching` are the operations
// exposed by Azure Quantum Resource Estimator. These will instruct
// resource counting such that the if-block will be executed
// only once, its resources will be cached, and appended in
// every other iteration.
if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
Controlled oracle([c], (1 <<< idx, eigenstateRegister));
EndEstimateCaching();
}
R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
}
if MResetZ(c) == One {
frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
}
}
// Return all the qubits used for oracles eigenstate back to 0 state
// using Microsoft.Quantum.Intrinsic.ResetAll.
ResetAll(eigenstateRegister);
return frequencyEstimate;
}
/// # Summary
/// Interprets `target` as encoding unsigned little-endian integer k
/// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
/// p is `power`, g is `generator` and N is `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order ( period )
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## power
/// Power of `generator` by which `target` is multiplied.
/// ## target
/// Register interpreted as little endian encoded which is multiplied by
/// given power of the generator. The multiplication is performed modulo
/// `modulus`.
internal operation ApplyOrderFindingOracle(
generator : Int, modulus : Int, power : Int, target : Qubit[]
)
: Unit
is Adj + Ctl {
// The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
// also use `ExpModI` to compute a by which x must be multiplied. Also
// note that we interpret target as unsigned integer in little-endian
// encoding.
ModularMultiplyByConstant(modulus,
ExpModI(generator, power, modulus),
target);
}
/// # Summary
/// Performs modular in-place multiplication by a classical constant.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(c*x) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular multiplication
/// ## c
/// Constant by which to multiply |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
use qs = Qubit[Length(y)];
for (idx, yq) in Enumerated(y) {
let shiftedC = (c <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
}
ApplyToEachCA(SWAP, Zipped(y, qs));
let invC = InverseModI(c, modulus);
for (idx, yq) in Enumerated(y) {
let shiftedC = (invC <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
}
}
/// # Summary
/// Performs modular in-place addition of a classical constant into a
/// quantum register.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(x+c) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular addition
/// ## c
/// Constant to add to |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
body (...) {
Controlled ModularAddConstant([], (modulus, c, y));
}
controlled (ctrls, ...) {
// We apply a custom strategy to control this operation instead of
// letting the compiler create the controlled variant for us in which
// the `Controlled` functor would be distributed over each operation
// in the body.
//
// Here we can use some scratch memory to save ensure that at most one
// control qubit is used for costly operations such as `AddConstant`
// and `CompareGreaterThenOrEqualConstant`.
if Length(ctrls) >= 2 {
use control = Qubit();
within {
Controlled X(ctrls, control);
} apply {
Controlled ModularAddConstant([control], (modulus, c, y));
}
} else {
use carry = Qubit();
Controlled AddConstant(ctrls, (c, y + [carry]));
Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
Controlled AddConstant([carry], (modulus, y));
Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
}
}
}
/// # Summary
/// Performs in-place addition of a constant into a quantum register.
///
/// # Description
/// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
/// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
///
/// # Input
/// ## c
/// Constant number to add to |𝑦⟩.
/// ## y
/// Quantum register of second summand and target; must not be empty.
internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
// We are using this version instead of the library version that is based
// on Fourier angles to show an advantage of sparse simulation in this sample.
let n = Length(y);
Fact(n > 0, "Bit width must be at least 1");
Fact(c >= 0, "constant must not be negative");
Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");
if c != 0 {
// If c has j trailing zeroes than the j least significant bits
// of y won't be affected by the addition and can therefore be
// ignored by applying the addition only to the other qubits and
// shifting c accordingly.
let j = NTrailingZeroes(c);
use x = Qubit[n - j];
within {
ApplyXorInPlace(c >>> j, x);
} apply {
IncByLE(x, y[j...]);
}
}
}
/// # Summary
/// Performs greater-than-or-equals comparison to a constant.
///
/// # Description
/// Toggles output qubit `target` if and only if input register `x`
/// is greater than or equal to `c`.
///
/// # Input
/// ## c
/// Constant value for comparison.
/// ## x
/// Quantum register to compare against.
/// ## target
/// Target qubit for comparison result.
///
/// # Reference
/// This construction is described in [Lemma 3, arXiv:2201.10200]
internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
: Unit is Adj+Ctl {
let bitWidth = Length(x);
if c == 0 {
X(target);
} elif c >= 2 ^ bitWidth {
// do nothing
} elif c == 2 ^ (bitWidth - 1) {
ApplyLowTCNOT(Tail(x), target);
} else {
// normalize constant
let l = NTrailingZeroes(c);
let cNormalized = c >>> l;
let xNormalized = x[l...];
let bitWidthNormalized = Length(xNormalized);
let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));
use qs = Qubit[bitWidthNormalized - 1];
let cs1 = [Head(xNormalized)] + Most(qs);
let cs2 = Rest(xNormalized);
within {
for i in IndexRange(gates) {
(gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
}
} apply {
ApplyLowTCNOT(Tail(qs), target);
}
}
}
/// # Summary
/// Internal operation used in the implementation of GreaterThanOrEqualConstant.
internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
within {
ApplyToEachA(X, [control1, control2]);
} apply {
ApplyAnd(control1, control2, target);
X(target);
}
}
internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
: Unit is Adj {
body (...) {
CCNOT(control1, control2, target);
}
adjoint (...) {
H(target);
if (M(target) == One) {
X(target);
CZ(control1, control2);
}
}
}
/// # Summary
/// Returns the number of trailing zeroes of a number
///
/// ## Example
/// ```qsharp
/// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
/// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
/// ```
internal function NTrailingZeroes(number : Int) : Int {
mutable nZeroes = 0;
mutable copy = number;
while (copy % 2 == 0) {
nZeroes += 1;
copy /= 2;
}
return nZeroes;
}
/// # Summary
/// An implementation for `CNOT` that when controlled using a single control uses
/// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
body (...) {
CNOT(a, b);
}
adjoint self;
controlled (ctls, ...) {
// In this application this operation is used in a way that
// it is controlled by at most one qubit.
Fact(Length(ctls) <= 1, "At most one control line allowed");
if IsEmpty(ctls) {
CNOT(a, b);
} else {
use q = Qubit();
within {
ApplyAnd(Head(ctls), a, q);
} apply {
CNOT(q, b);
}
}
}
controlled adjoint self;
}
Spuštění estimátoru prostředků
Estimátor prostředků nabízí šest předdefinovaných parametrů qubitu, z nichž čtyři mají instrukční sady založené na bráně a dvě, které mají instrukční sadu Majorana. Nabízí také dva kódysurface_code oprav kvantových chyb a floquet_code.
V tomto příkladu spustíte estimátor prostředků pomocí parametru qubit_gate_us_e3 qubitu surface_code a kódu opravy kvantových chyb.
Vyberte Zobrazit –> Paleta příkazů a zadejte "prostředek", který by měl vyvolat možnost Q#: Vypočítat odhady zdrojů. Můžete také kliknout na Odhad v seznamu příkazů zobrazených přímo před
Mainoperací. Tuto možnost vyberte, pokud chcete otevřít okno Nástroje pro posouzení prostředků.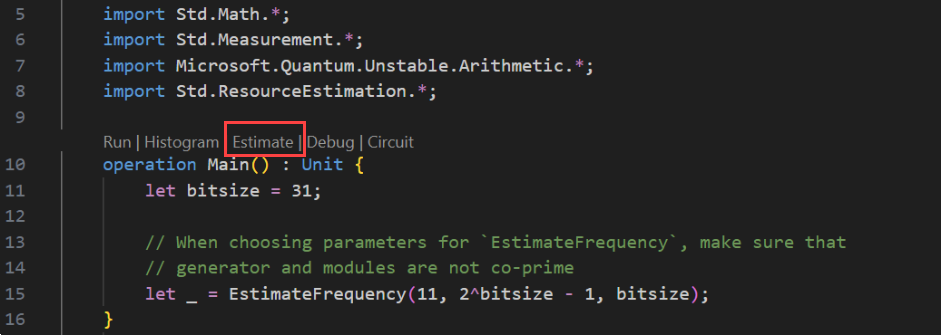
Pokud chcete odhadnout prostředky, můžete vybrat jeden nebo více parametrů Qubitu + typ kódu opravy chyb. V tomto příkladu vyberte qubit_gate_us_e3 a klikněte na TLAČÍTKO OK.
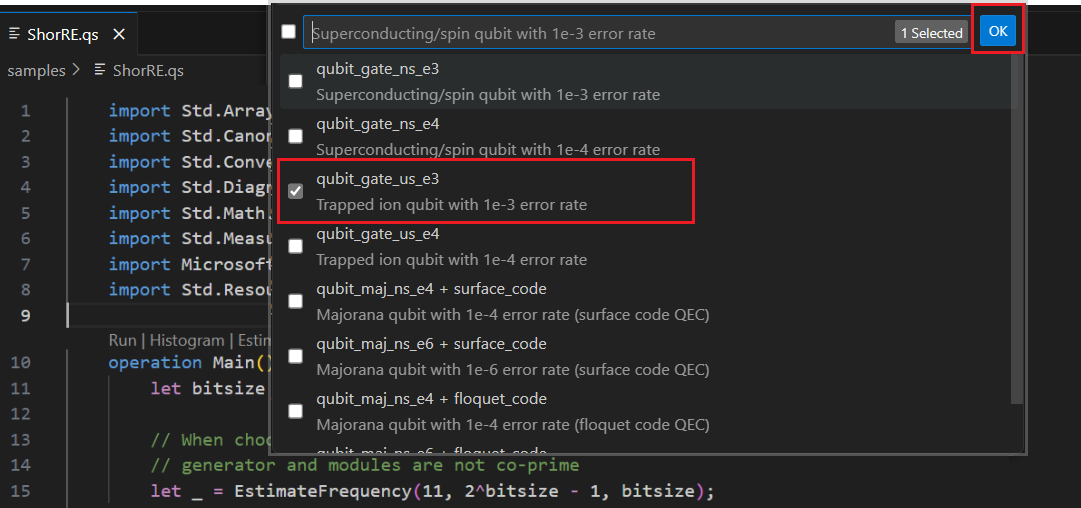
Zadejte rozpočet chyby nebo přijměte výchozí hodnotu 0.001. V tomto příkladu ponechte výchozí hodnotu a stiskněte Enter.
Stisknutím klávesy Enter přijměte výchozí název výsledku na základě názvu souboru, v tomto případě ShorRE.
Zobrazení výsledků
Estimátor prostředků poskytuje několik odhadů pro stejný algoritmus, přičemž každý zobrazuje kompromisy mezi počtem qubitů a modulem runtime. Pochopení kompromisu mezi modulem runtime a škálováním systému je jedním z důležitějších aspektů odhadu prostředků.
Výsledek odhadu zdroje se zobrazí v okně odhadu Q#.
Na kartě Výsledky se zobrazí souhrn odhadu zdrojů. Kliknutím na ikonu vedle prvního řádku vyberte sloupce, které chcete zobrazit. Můžete si vybrat z názvu spuštění, typu odhadu, typu qubitu, schématu qec, rozpočtu chyb, logických qubitů, logické hloubky, vzdálenosti kódu, T stavů, továren T, zlomku výroby, modulu runtime, rQOPS a fyzických qubitů.
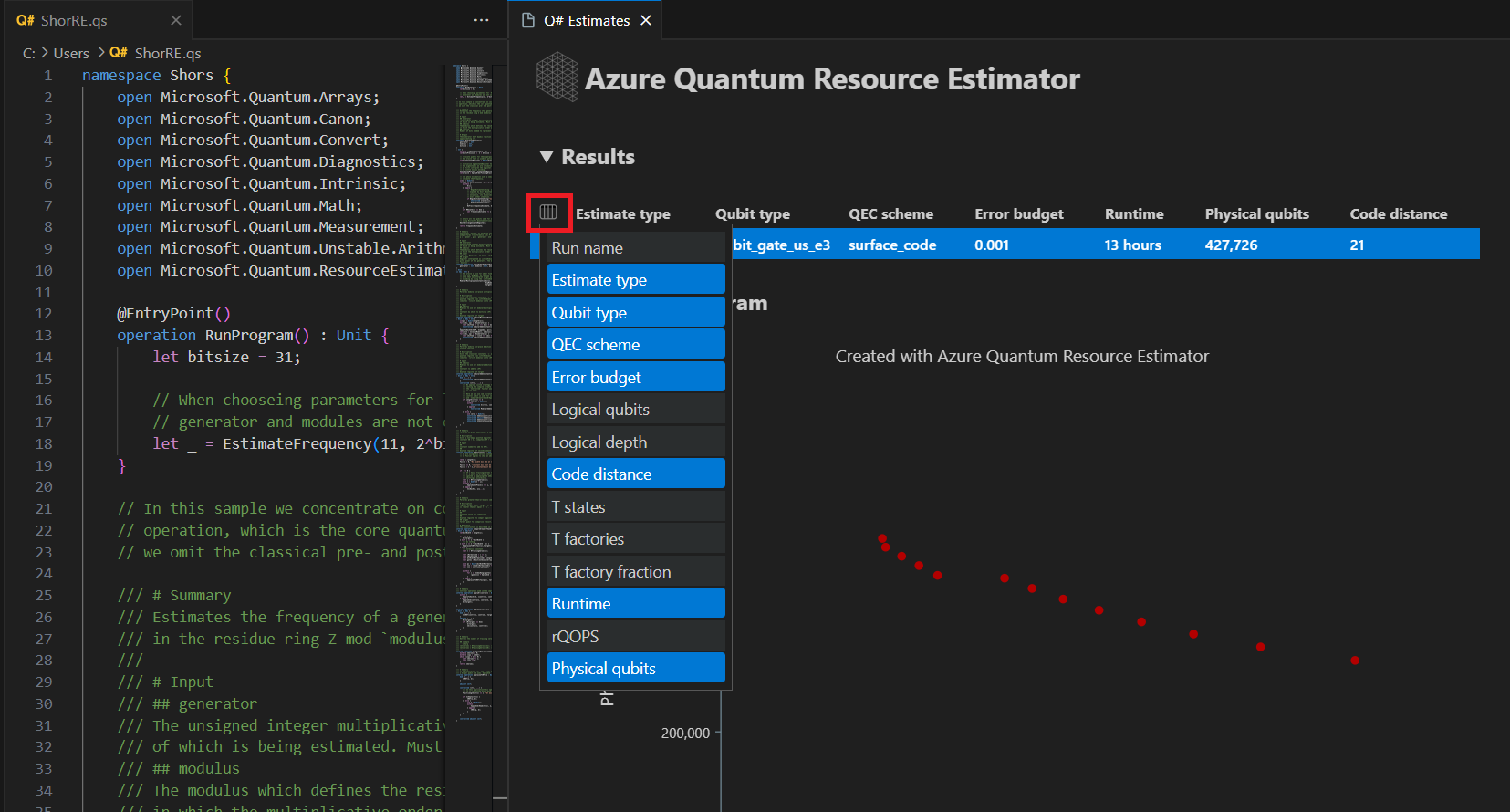
Ve sloupci Typ odhadu v tabulce výsledků můžete zobrazit počet optimálních kombinací {number of qubits, runtime} pro váš algoritmus. Tyto kombinace lze vidět v diagramu prostorového času.
Diagram prostorového času znázorňuje kompromisy mezi počtem fyzických qubitů a modulem runtime algoritmu. V tomto případě estimátor prostředků najde 13 různých optimálních kombinací z mnoha tisíc možných kombinací. Když najedete myší na každý {počet qubitů, bod runtime}, zobrazí se podrobnosti odhadu prostředků v tomto okamžiku.
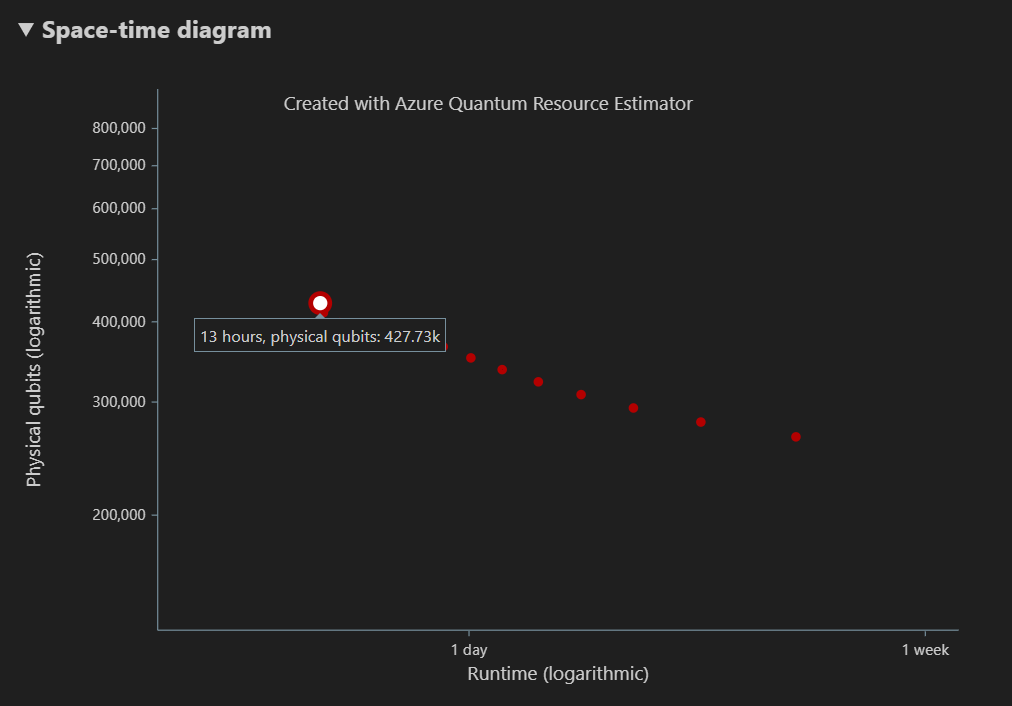
Další informace najdete v diagramu prostorového času.
Poznámka:
Pokud chcete zobrazit diagram prostoru a podrobnosti odhadu prostředků odpovídající danému bodu, musíte kliknout na jeden bod v diagramu prostorového času, tj. {počet qubitů, modul runtime}.
Diagram prostorů znázorňuje distribuci fyzických qubitů používaných pro algoritmus a továrny T, které odpovídají {počtu qubitů, modulu runtime}. Pokud například v diagramu prostorového času vyberete levý bod, počet fyzických qubitů potřebných ke spuštění algoritmu je 427726, 196686, z nichž jsou qubity algoritmů a 231040, z nichž jsou qubity T factory.
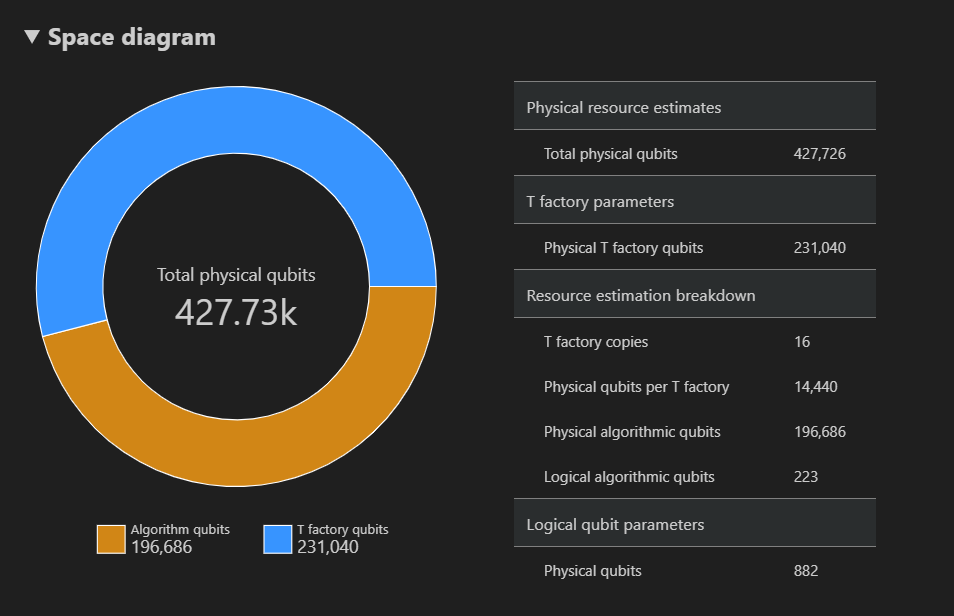
Nakonec na kartě Odhady zdrojů se zobrazí úplný seznam výstupních dat pro nástroj pro odhad prostředků odpovídající {počtu qubitů, modulu runtime} . Podrobnosti o nákladech můžete zkontrolovat sbalením skupin, které obsahují další informace. Vyberte například levý bod v diagramu prostorového času a sbalte skupinu parametrů logického qubitu.
Parametr logického qubitu Hodnota Schéma QEC surface_code Vzdálenost kódu 21 Fyzické qubity 882 Logická doba cyklu 13 milisekund Míra chyb logického qubitu 3.00E-13 Přechod předfaktorem 0.03 Prahová hodnota opravy chyb 0,01 Vzorec času logického cyklu (4 * twoQubitGateTime+ 2 *oneQubitMeasurementTime) *codeDistanceVzorec fyzických qubitů 2 * codeDistance*codeDistanceTip
Kliknutím na Zobrazit podrobné řádky zobrazíte popis každého výstupu dat sestavy.
Další informace najdete v úplných datech sestavy nástroje pro odhad prostředků.
target Změna parametrů
Náklady na stejný program Q# můžete odhadnout pomocí jiného typu qubitu, kódu opravy chyb a rozpočtu chyb. Otevřete okno Estimátoru zdrojů výběrem možnosti Zobrazit –> Paleta příkazů a zadejte Q#: Calculate Resource Estimates.
Vyberte jakoukoli jinou konfiguraci, například parametr qubitu založený na Majorana. qubit_maj_ns_e6 Přijměte výchozí hodnotu rozpočtu chyby nebo zadejte novou hodnotu a stiskněte Enter. Estimátor prostředků znovu spustí odhad s novými target parametry.
Další informace najdete v parametrech Target pro estimátor prostředků.
Spuštění více konfigurací parametrů
Estimátor prostředků Azure Quantum může spustit více konfigurací parametrů a porovnat výsledky odhadu target prostředků.
Vyberte Zobrazení –> Paleta příkazů nebo stiskněte Kombinaci kláves Ctrl+Shift+P a zadejte
Q#: Calculate Resource Estimates.Vyberte qubit_gate_us_e3, qubit_gate_us_e4, qubit_maj_ns_e4 + floquet_code a qubit_maj_ns_e6 + floquet_code a klikněte na tlačítko OK.
Přijměte výchozí hodnotu rozpočtu chyby 0,001 a stiskněte Enter.
Stisknutím klávesy Enter přijměte vstupní soubor, v tomto případě ShorRE.qs.
V případě více konfigurací parametrů se výsledky zobrazí v různých řádcích na kartě Výsledky .
Diagram prostorového času zobrazuje výsledky pro všechny konfigurace parametrů. První sloupec tabulky výsledků zobrazí legendu pro každou konfiguraci parametrů. Když na každý bod najedete myší, zobrazí se podrobnosti odhadu zdrojů v tomto okamžiku.
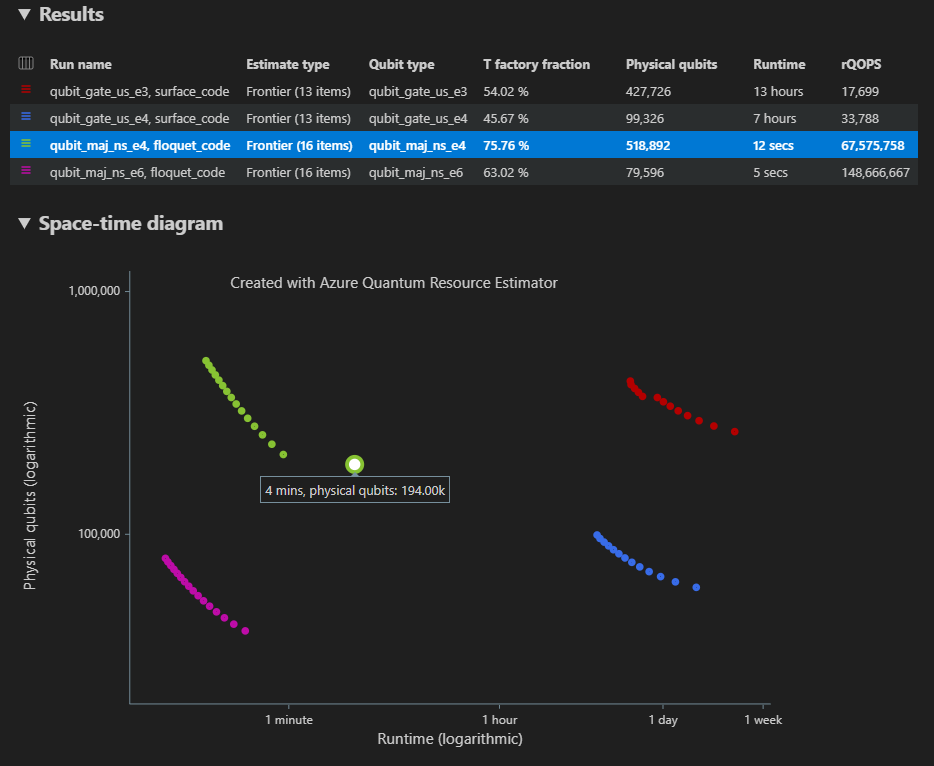
Klikněte na {number of qubits, runtime} point of the space-time diagram to bring up the corresponding space diagram and report data.
Požadavky pro poznámkový blok Jupyter v editoru VS Code
Prostředí Pythonu s nainstalovaným Pythonem a Pipem
Nejnovější verze editoru Visual Studio Code nebo otevření editoru VS Code na webu
VS Code s nainstalovanými rozšířeními Quantum Development Kit, Pythona Jupyter.
Nejnovější balíčky a
qsharpslužby Azure Quantumqsharp_widgets.python -m pip install --upgrade qsharp qsharp_widgetsnebo
!pip install --upgrade qsharp qsharp_widgets
Tip
Ke spuštění nástroje pro odhad prostředků nemusíte mít účet Azure.
Vytvoření kvantového algoritmu
Ve VS Code vyberte > Zobrazit příkaz a vyberte Vytvořit: Nový poznámkový blok Jupyter.
V pravém horním rohu nástroj VS Code rozpozná a zobrazí verzi Pythonu a virtuálního prostředí Pythonu, které bylo vybráno pro poznámkový blok. Pokud máte více prostředí Pythonu, možná budete muset vybrat jádro pomocí nástroje pro výběr jádra v pravém horním rohu. Pokud nebylo zjištěno žádné prostředí, informace o nastavení najdete v poznámkových blocích Jupyter v editoru VS Code .
V první buňce poznámkového bloku naimportujte
qsharpbalíček.import qsharpPřidejte novou buňku a zkopírujte následující kód.
%%qsharp import Std.Arrays.*; import Std.Canon.*; import Std.Convert.*; import Std.Diagnostics.*; import Std.Math.*; import Std.Measurement.*; import Microsoft.Quantum.Unstable.Arithmetic.*; import Std.ResourceEstimation.*; operation RunProgram() : Unit { let bitsize = 31; // When choosing parameters for `EstimateFrequency`, make sure that // generator and modules are not co-prime let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize); } // In this sample we concentrate on costing the `EstimateFrequency` // operation, which is the core quantum operation in Shors algorithm, and // we omit the classical pre- and post-processing. /// # Summary /// Estimates the frequency of a generator /// in the residue ring Z mod `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order (period) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## bitsize /// Number of bits needed to represent the modulus. /// /// # Output /// The numerator k of dyadic fraction k/2^bitsPrecision /// approximating s/r. operation EstimateFrequency( generator : Int, modulus : Int, bitsize : Int ) : Int { mutable frequencyEstimate = 0; let bitsPrecision = 2 * bitsize + 1; // Allocate qubits for the superposition of eigenstates of // the oracle that is used in period finding. use eigenstateRegister = Qubit[bitsize]; // Initialize eigenstateRegister to 1, which is a superposition of // the eigenstates we are estimating the phases of. // We first interpret the register as encoding an unsigned integer // in little endian encoding. ApplyXorInPlace(1, eigenstateRegister); let oracle = ApplyOrderFindingOracle(generator, modulus, _, _); // Use phase estimation with a semiclassical Fourier transform to // estimate the frequency. use c = Qubit(); for idx in bitsPrecision - 1..-1..0 { within { H(c); } apply { // `BeginEstimateCaching` and `EndEstimateCaching` are the operations // exposed by Azure Quantum Resource Estimator. These will instruct // resource counting such that the if-block will be executed // only once, its resources will be cached, and appended in // every other iteration. if BeginEstimateCaching("ControlledOracle", SingleVariant()) { Controlled oracle([c], (1 <<< idx, eigenstateRegister)); EndEstimateCaching(); } R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c); } if MResetZ(c) == One { frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx); } } // Return all the qubits used for oracle eigenstate back to 0 state // using Microsoft.Quantum.Intrinsic.ResetAll. ResetAll(eigenstateRegister); return frequencyEstimate; } /// # Summary /// Interprets `target` as encoding unsigned little-endian integer k /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where /// p is `power`, g is `generator` and N is `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order ( period ) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## power /// Power of `generator` by which `target` is multiplied. /// ## target /// Register interpreted as little endian encoded which is multiplied by /// given power of the generator. The multiplication is performed modulo /// `modulus`. internal operation ApplyOrderFindingOracle( generator : Int, modulus : Int, power : Int, target : Qubit[] ) : Unit is Adj + Ctl { // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We // also use `ExpModI` to compute a by which x must be multiplied. Also // note that we interpret target as unsigned integer in little-endian // encoding. ModularMultiplyByConstant(modulus, ExpModI(generator, power, modulus), target); } /// # Summary /// Performs modular in-place multiplication by a classical constant. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(c*x) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular multiplication /// ## c /// Constant by which to multiply |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { use qs = Qubit[Length(y)]; for (idx, yq) in Enumerated(y) { let shiftedC = (c <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, shiftedC, qs)); } ApplyToEachCA(SWAP, Zipped(y, qs)); let invC = InverseModI(c, modulus); for (idx, yq) in Enumerated(y) { let shiftedC = (invC <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs)); } } /// # Summary /// Performs modular in-place addition of a classical constant into a /// quantum register. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(x+c) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular addition /// ## c /// Constant to add to |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { body (...) { Controlled ModularAddConstant([], (modulus, c, y)); } controlled (ctrls, ...) { // We apply a custom strategy to control this operation instead of // letting the compiler create the controlled variant for us in which // the `Controlled` functor would be distributed over each operation // in the body. // // Here we can use some scratch memory to save ensure that at most one // control qubit is used for costly operations such as `AddConstant` // and `CompareGreaterThenOrEqualConstant`. if Length(ctrls) >= 2 { use control = Qubit(); within { Controlled X(ctrls, control); } apply { Controlled ModularAddConstant([control], (modulus, c, y)); } } else { use carry = Qubit(); Controlled AddConstant(ctrls, (c, y + [carry])); Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry])); Controlled AddConstant([carry], (modulus, y)); Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry)); } } } /// # Summary /// Performs in-place addition of a constant into a quantum register. /// /// # Description /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩. /// /// # Input /// ## c /// Constant number to add to |𝑦⟩. /// ## y /// Quantum register of second summand and target; must not be empty. internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl { // We are using this version instead of the library version that is based // on Fourier angles to show an advantage of sparse simulation in this sample. let n = Length(y); Fact(n > 0, "Bit width must be at least 1"); Fact(c >= 0, "constant must not be negative"); Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}"); if c != 0 { // If c has j trailing zeroes than the j least significant bits // of y will not be affected by the addition and can therefore be // ignored by applying the addition only to the other qubits and // shifting c accordingly. let j = NTrailingZeroes(c); use x = Qubit[n - j]; within { ApplyXorInPlace(c >>> j, x); } apply { IncByLE(x, y[j...]); } } } /// # Summary /// Performs greater-than-or-equals comparison to a constant. /// /// # Description /// Toggles output qubit `target` if and only if input register `x` /// is greater than or equal to `c`. /// /// # Input /// ## c /// Constant value for comparison. /// ## x /// Quantum register to compare against. /// ## target /// Target qubit for comparison result. /// /// # Reference /// This construction is described in [Lemma 3, arXiv:2201.10200] internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit) : Unit is Adj+Ctl { let bitWidth = Length(x); if c == 0 { X(target); } elif c >= 2 ^ bitWidth { // do nothing } elif c == 2 ^ (bitWidth - 1) { ApplyLowTCNOT(Tail(x), target); } else { // normalize constant let l = NTrailingZeroes(c); let cNormalized = c >>> l; let xNormalized = x[l...]; let bitWidthNormalized = Length(xNormalized); let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized)); use qs = Qubit[bitWidthNormalized - 1]; let cs1 = [Head(xNormalized)] + Most(qs); let cs2 = Rest(xNormalized); within { for i in IndexRange(gates) { (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]); } } apply { ApplyLowTCNOT(Tail(qs), target); } } } /// # Summary /// Internal operation used in the implementation of GreaterThanOrEqualConstant. internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { within { ApplyToEachA(X, [control1, control2]); } apply { ApplyAnd(control1, control2, target); X(target); } } internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { body (...) { CCNOT(control1, control2, target); } adjoint (...) { H(target); if (M(target) == One) { X(target); CZ(control1, control2); } } } /// # Summary /// Returns the number of trailing zeroes of a number /// /// ## Example /// ```qsharp /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0 /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2 /// ``` internal function NTrailingZeroes(number : Int) : Int { mutable nZeroes = 0; mutable copy = number; while (copy % 2 == 0) { nZeroes += 1; copy /= 2; } return nZeroes; } /// # Summary /// An implementation for `CNOT` that when controlled using a single control uses /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7. internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl { body (...) { CNOT(a, b); } adjoint self; controlled (ctls, ...) { // In this application this operation is used in a way that // it is controlled by at most one qubit. Fact(Length(ctls) <= 1, "At most one control line allowed"); if IsEmpty(ctls) { CNOT(a, b); } else { use q = Qubit(); within { ApplyAnd(Head(ctls), a, q); } apply { CNOT(q, b); } } } controlled adjoint self; }
Odhad kvantového algoritmu
Teď pomocí výchozích předpokladů odhadnete fyzické prostředky pro RunProgram operaci. Přidejte novou buňku a zkopírujte následující kód.
result = qsharp.estimate("RunProgram()")
result
Funkce qsharp.estimate vytvoří výsledný objekt, který lze použít k zobrazení tabulky s celkovými počty fyzických prostředků. Podrobnosti o nákladech můžete zkontrolovat rozbalením skupin, které obsahují další informace. Další informace najdete v úplných datech sestavy nástroje pro odhad prostředků.
Rozbalte například parametry logického qubitu skupinu, abyste viděli, že vzdálenost kódu je 21 a počet fyzických qubitů je 882.
| Parametr logického qubitu | Hodnota |
|---|---|
| Schéma QEC | surface_code |
| Vzdálenost kódu | 21 |
| Fyzické qubity | 882 |
| Logická doba cyklu | 8 milisekund |
| Míra chyb logického qubitu | 3.00E-13 |
| Přechod předfaktorem | 0.03 |
| Prahová hodnota opravy chyb | 0,01 |
| Vzorec času logického cyklu | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Vzorec fyzických qubitů | 2 * codeDistance * codeDistance |
Tip
Pro kompaktnější verzi výstupní tabulky můžete použít result.summary.
Prostorový diagram
Distribuce fyzických qubitů používaných pro algoritmus a T factory je faktor, který může ovlivnit návrh vašeho algoritmu. Balíček můžete použít qsharp-widgets k vizualizaci této distribuce, abyste lépe pochopili odhadované požadavky na prostor pro algoritmus.
from qsharp-widgets import SpaceChart, EstimateDetails
SpaceChart(result)
V tomto příkladu je počet fyzických qubitů potřebných ke spuštění algoritmu 829766, 196686 jsou qubity algoritmů a 633080, z nichž jsou qubity T factory.
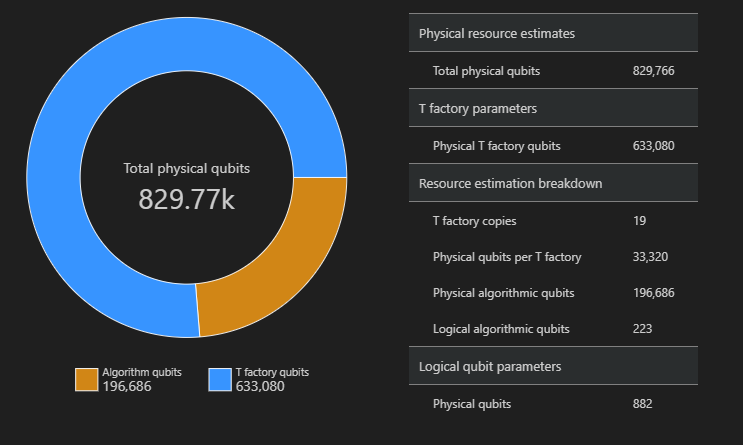
Změna výchozích hodnot a odhad algoritmu
Při odesílání žádosti o odhad prostředků pro váš program můžete zadat některé volitelné parametry.
jobParams Pomocí tohoto pole získáte přístup ke všem target parametrům, které je možné předat spuštění úlohy, a zjistit, které výchozí hodnoty se předpokládaly:
result['jobParams']
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Můžete vidět, že estimátor prostředků vezme qubit_gate_ns_e3 qubitový model, surface_code kód opravy chyb a rozpočet chyb 0.001 jako výchozí hodnoty odhadu.
Toto jsou target parametry, které je možné přizpůsobit:
-
errorBudget– celkový povolený rozpočet chyb pro algoritmus -
qecScheme– schéma opravy kvantových chyb (QEC) -
qubitParams– parametry fyzického qubitu -
constraints- omezení na úrovni součásti -
distillationUnitSpecifications- specifikace pro algoritmy pro destilační algoritmy t továren -
estimateType- jednoduchá nebo hraniční
Další informace najdete v parametrech Target pro estimátor prostředků.
Změna modelu qubitu
Náklady na stejný algoritmus můžete odhadnout pomocí parametru qubitu založeného na Majorana, qubitParams"qubit_maj_ns_e6".
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
}})
EstimateDetails(result_maj)
Změna schématu oprav kvantových chyb
Úlohu odhadu prostředků můžete znovu spustit pro stejný příklad na parametrech qubitu založeného na majoraně se schématem QEC s floquedem. qecScheme
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
}})
EstimateDetails(result_maj)
Změna rozpočtu chyb
V dalším kroku znovu spusťte stejný kvantový obvod s errorBudget 10 %.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
},
"errorBudget": 0.1})
EstimateDetails(result_maj)
Dávkování pomocí nástroje pro odhad prostředků
Estimátor prostředků Azure Quantum umožňuje spustit více konfigurací target parametrů a porovnat výsledky. To je užitečné, když chcete porovnat náklady na různé modely qubitů, schémata QEC nebo rozpočty chyb.
Odhad dávky můžete provést předáním seznamu target parametrů parametru
paramsqsharp.estimatefunkce. Například spusťte stejný algoritmus s výchozími parametry a parametry qubitu založeným na Majorana se schématem QEC floquet.result_batch = qsharp.estimate("RunProgram()", params= [{}, # Default parameters { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" } }]) result_batch.summary_data_frame(labels=["Gate-based ns, 10⁻³", "Majorana ns, 10⁻⁶"])Model Logické qubity Logická hloubka Stavy T Vzdálenost kódu T factory Zlomek továrny T Fyzické qubity rQOPS Fyzický modul runtime Vrátná ns, 10⁻³ 223 3,64M 4.70M 21 19 76.30 % 829,77k 26,55 M 31 sekund Majorana ns, 10⁻⁶ 223 3,64M 4.70M 5 19 63.02 % 79,60k 148.67M 5 sekund -
from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"] params = EstimatorParams(num_items=6) params.error_budget = 0.333 params.items[0].qubit_params.name = QubitParams.GATE_US_E3 params.items[1].qubit_params.name = QubitParams.GATE_US_E4 params.items[2].qubit_params.name = QubitParams.GATE_NS_E3 params.items[3].qubit_params.name = QubitParams.GATE_NS_E4 params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4 params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6 params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODEqsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)Model Logické qubity Logická hloubka Stavy T Vzdálenost kódu T factory Zlomek továrny T Fyzické qubity rQOPS Fyzický modul runtime μs, 10⁻³ 223 3.64M 4.70M 17 13 40.54 % 216,77k 21,86k 10 hodin μs, 10⁻⁴ 223 3,64M 4.70M 9 14 43.17 % 63,57k 41,30k 5 hodin Vrátná ns, 10⁻³ 223 3.64M 4.70M 17 16 69.08 % 416,89k 32,79 M 25 sekund Ns, 10⁻⁴ 223 3.64M 4.70M 9 14 43.17 % 63,57k 61,94M 13 sekund Majorana ns, 10⁻⁴ 223 3.64M 4.70M 9 19 82.75 % 501,48k 82,59 M 10 sekund Majorana ns, 10⁻⁶ 223 3.64M 4.70M 5 13 31.47 % 42,96k 148.67M 5 sekund
Odhad běhu paretovy hranice
Při odhadu prostředků algoritmu je důležité zvážit kompromis mezi počtem fyzických qubitů a modulem runtime algoritmu. Můžete zvážit přidělení co největšího počtu fyzických qubitů, abyste snížili dobu běhu algoritmu. Počet fyzických qubitů je však omezený počtem fyzických qubitů dostupných v kvantovém hardwaru.
Odhad paretovy hranice poskytuje více odhadů pro stejný algoritmus, přičemž každý má kompromis mezi počtem qubitů a modulem runtime.
Pokud chcete spustit estimátor prostředků pomocí odhadu paretovské hranice, musíte parametr zadat
"estimateType"target jako"frontier". Například spusťte stejný algoritmus s parametry qubitu založeným na Majorana s povrchovým kódem pomocí odhadu paretovy hranice.result = qsharp.estimate("RunProgram()", params= {"qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # frontier estimation } )Pomocí funkce můžete
EstimatesOverviewzobrazit tabulku s celkovými počty fyzických prostředků. Kliknutím na ikonu vedle prvního řádku vyberte sloupce, které chcete zobrazit. Můžete si vybrat z názvu spuštění, typu odhadu, typu qubitu, schématu qec, rozpočtu chyb, logických qubitů, logické hloubky, vzdálenosti kódu, T stavů, továren T, zlomku výroby, modulu runtime, rQOPS a fyzických qubitů.from qsharp_widgets import EstimatesOverview EstimatesOverview(result)
Ve sloupci Typ odhadu v tabulce výsledků uvidíte počet různých kombinací {number of qubits, runtime} pro váš algoritmus. V tomto případě estimátor prostředků najde 22 různých optimálních kombinací z mnoha tisíc možných kombinací.
Diagram prostorového času
Tato EstimatesOverview funkce také zobrazuje diagram prostorového času nástroje pro odhad prostředků.
Diagram prostorového času zobrazuje počet fyzických qubitů a modul runtime algoritmu pro každý {počet qubitů, modul runtime}. Když na každý bod najedete myší, zobrazí se podrobnosti odhadu zdrojů v tomto okamžiku.
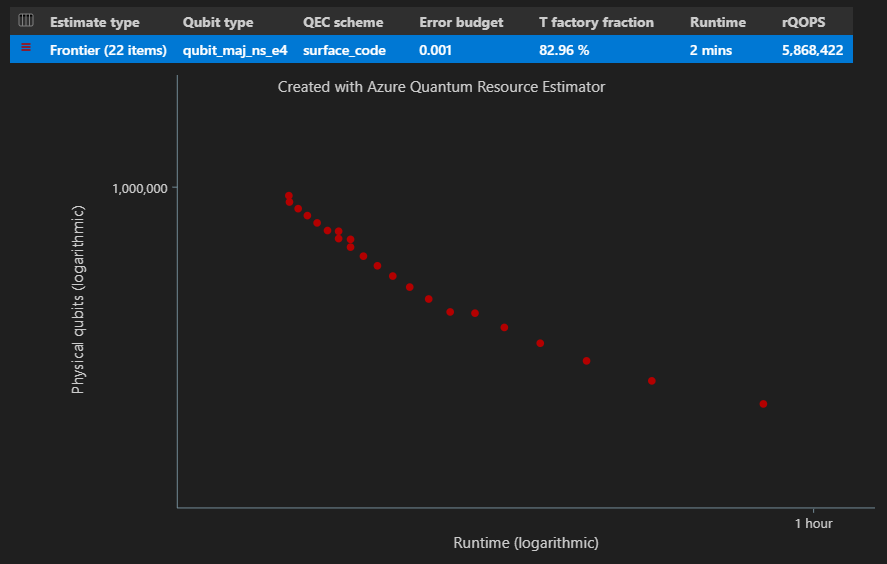
Dávkování s odhadem hranice Paretova hranice
Pokud chcete odhadnout a porovnat více konfigurací target parametrů s odhadem hranice, přidejte
"estimateType": "frontier",je k parametrům.result = qsharp.estimate( "RunProgram()", [ { "qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # Pareto frontier estimation }, { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" }, "estimateType": "frontier", # Pareto frontier estimation }, ] ) EstimatesOverview(result, colors=["#1f77b4", "#ff7f0e"], runNames=["e4 Surface Code", "e6 Floquet Code"])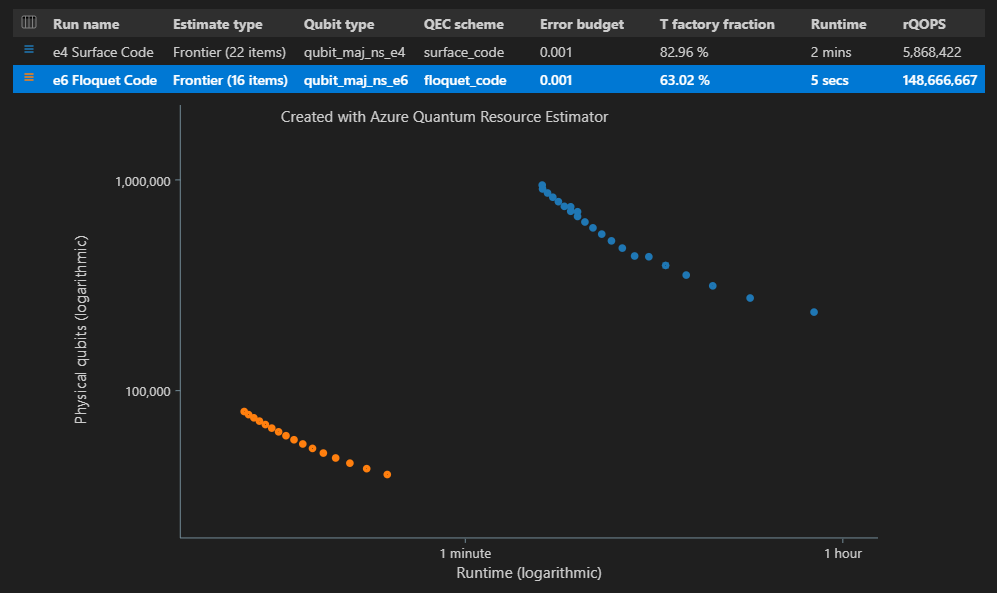
Poznámka:
Pomocí funkce můžete definovat barvy a názvy spuštění pro diagram
EstimatesOverviewqubit-time.Při spouštění více konfigurací parametrů pomocí odhadu target paretovské hranice můžete zobrazit odhady prostředků pro konkrétní bod diagramu prostorového času, který je určený pro každý {počet qubitů, modul runtime}. Následující kód například ukazuje využití podrobností odhadu pro druhé spuštění (odhad index=0) a čtvrtý modul runtime (index bodu =3).
EstimateDetails(result[1], 4)Můžete si také prohlédnout diagram prostoru pro konkrétní bod diagramu prostorového času. Například následující kód ukazuje diagram prostoru pro první spuštění kombinací (odhad index=0) a třetí nejkratší modul runtime (index bodu=2).
SpaceChart(result[0], 2)
Požadavky pro Qiskit ve Visual Studio Code
Prostředí Pythonu s nainstalovaným Pythonem a Pipem
Nejnovější verze Visual Studio Code nebo otevřete Visual Studio Code na webu.
VS Code s nainstalovanými rozšířeními Quantum Development Kit, Pythona Jupyter.
Nejnovější balíčky Azure Quantum
qsharpaqsharp_widgetsaqiskit.python -m pip install --upgrade qsharp qsharp_widgets qiskitnebo
!pip install --upgrade qsharp qsharp_widgets qiskit
Tip
Ke spuštění nástroje pro odhad prostředků nemusíte mít účet Azure.
Vytvoření nového poznámkového bloku Jupyter
- Ve VS Code vyberte > Zobrazit příkaz a vyberte Vytvořit: Nový poznámkový blok Jupyter.
- V pravém horním rohu nástroj VS Code rozpozná a zobrazí verzi Pythonu a virtuálního prostředí Pythonu, které bylo vybráno pro poznámkový blok. Pokud máte více prostředí Pythonu, možná budete muset vybrat jádro pomocí nástroje pro výběr jádra v pravém horním rohu. Pokud nebylo zjištěno žádné prostředí, informace o nastavení najdete v poznámkových blocích Jupyter v editoru VS Code .
Vytvoření kvantového algoritmu
V tomto příkladu vytvoříte kvantový obvod pro násobitel na základě konstrukce prezentované v Ruiz-Perez a Garcia-Escartin (arXiv:1411,5949), který používá k implementaci aritmetické transformace Quantum Fourier.
Velikost násobitele můžete upravit změnou bitwidth proměnné. Generování okruhu je zabaleno do funkce, kterou lze volat s bitwidth hodnotou násobitele. Operace bude mít dva vstupní registry, každou velikost zadaného bitwidtha jeden výstupní registr, který je dvakrát velikost zadaného bitwidth. Funkce také vytiskne několik logických prostředků pro násobitel extrahovaný přímo z kvantového okruhu.
from qiskit.circuit.library import RGQFTMultiplier
def create_algorithm(bitwidth):
print(f"[INFO] Create a QFT-based multiplier with bitwidth {bitwidth}")
circ = RGQFTMultiplier(num_state_qubits=bitwidth)
return circ
Poznámka:
Pokud vyberete jádro Pythonu a modul qiskit se nerozpozná, zkuste v nástroji pro výběr jádra vybrat jiné prostředí Pythonu.
Odhad kvantového algoritmu
Vytvořte instanci algoritmu pomocí create_algorithm funkce. Velikost násobitele můžete upravit změnou bitwidth proměnné.
bitwidth = 4
circ = create_algorithm(bitwidth)
Pomocí výchozích předpokladů odhadněte fyzické prostředky pro tuto operaci. Můžete použít volání estimate, které je přetížené a může přijmout QuantumCircuit objekt z Qiskit.
from qsharp.estimator import EstimatorParams
from qsharp.interop.qiskit import estimate
params = EstimatorParams()
result = estimate(circ, params)
Případně můžete použít ResourceEstimatorBackend k provedení odhadu, jak to dělá stávající back-end.
from qsharp.interop.qiskit import ResourceEstimatorBackend
from qsharp.estimator import EstimatorParams
params = EstimatorParams()
backend = ResourceEstimatorBackend()
job = backend.run(circ, params)
result = job.result()
Objekt result obsahuje výstup úlohy odhadu zdroje. Pomocí funkce EstimateDetails můžete zobrazit výsledky v čitelnějším formátu.
from qsharp_widgets import EstimateDetails
EstimateDetails(result)
EstimateDetails funkce zobrazí tabulku s celkovými počty fyzických prostředků. Podrobnosti o nákladech můžete zkontrolovat rozbalením skupin, které obsahují další informace. Další informace najdete v úplných datech sestavy nástroje pro odhad prostředků.
Pokud například rozbalíte skupinu parametrů logického qubitu, můžete snadněji zjistit, že vzdálenost kódu opravy chyb je 15.
| Parametr logického qubitu | Hodnota |
|---|---|
| Schéma QEC | surface_code |
| Vzdálenost kódu | 15 |
| Fyzické qubity | 450 |
| Logická doba cyklu | 6us |
| Míra chyb logického qubitu | 3.00E-10 |
| Přechod předfaktorem | 0.03 |
| Prahová hodnota opravy chyb | 0,01 |
| Vzorec času logického cyklu | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Vzorec fyzických qubitů | 2 * codeDistance * codeDistance |
Ve skupině fyzických parametrů qubitu můžete zobrazit vlastnosti fyzického qubitu, které byly pro tento odhad předpokládány. Například doba provedení měření jednoho qubitu a brána s jedním qubitem se předpokládá, že je 100 ns a 50 ns.
Tip
Pomocí metody result.data() můžete také získat přístup k výstupu Nástroje pro odhad prostředků jako slovník Pythonu. Například pro přístup k fyzickým počtům result.data()["physicalCounts"].
Diagramy mezer
Distribuce fyzických qubitů používaných pro algoritmus a T factory je faktor, který může ovlivnit návrh vašeho algoritmu. Tuto distribuci můžete vizualizovat, abyste lépe pochopili odhadované požadavky na prostor pro algoritmus.
from qsharp_widgets import SpaceChart
SpaceChart(result)
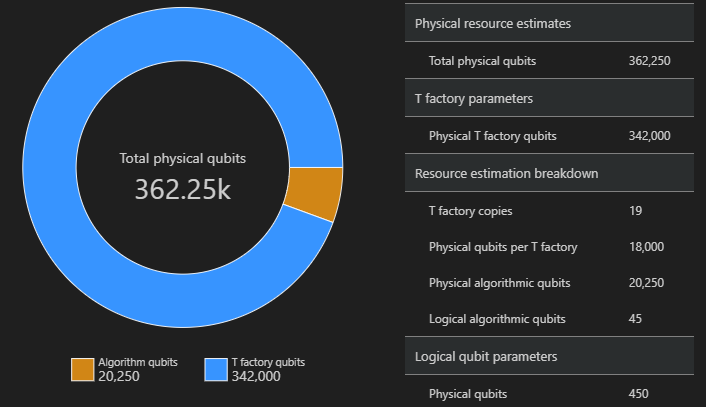
Diagram prostoru znázorňuje podíl qubitů algoritmu a qubitů t factory. Všimněte si, že počet kopií továrny T, 19, přispívá k počtu fyzických qubitů pro továrny T jako $\text{továrny T} \cdot \text{fyzický qubit na továrnu T} = 19 \cdot 18 000 = 342 000$.
Další informace naleznete v tématu Fyzický odhad T factory.
Změna výchozích hodnot a odhad algoritmu
Při odesílání žádosti o odhad prostředků pro váš program můžete zadat některé volitelné parametry.
jobParams Pole použijte pro přístup ke všem hodnotám, které je možné předat do provádění úlohy, a zjistěte, které výchozí hodnoty se předpokládaly:
result.data()["jobParams"]
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Toto jsou target parametry, které je možné přizpůsobit:
-
errorBudget– celkový povolený rozpočet chyb -
qecScheme– schéma opravy kvantových chyb (QEC) -
qubitParams– parametry fyzického qubitu -
constraints- omezení na úrovni součásti -
distillationUnitSpecifications- specifikace pro algoritmy pro destilační algoritmy t továren
Další informace najdete v parametrech Target pro estimátor prostředků.
Změna modelu qubitu
Dále pomocí parametru qubitu založeného na Majorana odhadněte náklady na stejný algoritmus. qubit_maj_ns_e6
qubitParams = {
"name": "qubit_maj_ns_e6"
}
result = backend.run(circ, qubitParams).result()
Počet fyzických počtů můžete zkontrolovat programově. Můžete například prozkoumat podrobnosti o objektu pro vytváření T, který byl vytvořen pro spuštění algoritmu.
result.data()["tfactory"]
{'eccDistancePerRound': [1, 1, 5],
'logicalErrorRate': 1.6833177305222897e-10,
'moduleNamePerRound': ['15-to-1 space efficient physical',
'15-to-1 RM prep physical',
'15-to-1 RM prep logical'],
'numInputTstates': 20520,
'numModulesPerRound': [1368, 20, 1],
'numRounds': 3,
'numTstates': 1,
'physicalQubits': 16416,
'physicalQubitsPerRound': [12, 31, 1550],
'runtime': 116900.0,
'runtimePerRound': [4500.0, 2400.0, 110000.0]}
Poznámka:
Ve výchozím nastavení se modul runtime zobrazuje v nanosekundách.
Tato data můžete použít k vytvoření některých vysvětlení, jak továrny T produkují požadované stavy T.
data = result.data()
tfactory = data["tfactory"]
breakdown = data["physicalCounts"]["breakdown"]
producedTstates = breakdown["numTfactories"] * breakdown["numTfactoryRuns"] * tfactory["numTstates"]
print(f"""A single T factory produces {tfactory["logicalErrorRate"]:.2e} T states with an error rate of (required T state error rate is {breakdown["requiredLogicalTstateErrorRate"]:.2e}).""")
print(f"""{breakdown["numTfactories"]} copie(s) of a T factory are executed {breakdown["numTfactoryRuns"]} time(s) to produce {producedTstates} T states ({breakdown["numTstates"]} are required by the algorithm).""")
print(f"""A single T factory is composed of {tfactory["numRounds"]} rounds of distillation:""")
for round in range(tfactory["numRounds"]):
print(f"""- {tfactory["numUnitsPerRound"][round]} {tfactory["unitNamePerRound"][round]} unit(s)""")
A single T factory produces 1.68e-10 T states with an error rate of (required T state error rate is 2.77e-08).
23 copies of a T factory are executed 523 time(s) to produce 12029 T states (12017 are required by the algorithm).
A single T factory is composed of 3 rounds of distillation:
- 1368 15-to-1 space efficient physical unit(s)
- 20 15-to-1 RM prep physical unit(s)
- 1 15-to-1 RM prep logical unit(s)
Změna schématu oprav kvantových chyb
Nyní znovu spusťte úlohu odhadu prostředků pro stejný příklad na parametrech qubitu založeném na majoraně se schématem QEC floqued . qecScheme
params = {
"qubitParams": {"name": "qubit_maj_ns_e6"},
"qecScheme": {"name": "floquet_code"}
}
result_maj_floquet = backend.run(circ, params).result()
EstimateDetails(result_maj_floquet)
Změna rozpočtu chyb
Pojďme znovu spustit stejný kvantový okruh s errorBudget 10 %.
params = {
"errorBudget": 0.01,
"qubitParams": {"name": "qubit_maj_ns_e6"},
"qecScheme": {"name": "floquet_code"},
}
result_maj_floquet_e1 = backend.run(circ, params).result()
EstimateDetails(result_maj_floquet_e1)
Poznámka:
Pokud při práci s nástrojem pro odhad prostředků narazíte na nějaký problém, podívejte se na stránku Řešení potíží nebo se obraťte AzureQuantumInfo@microsoft.comna kontakt .