Math Primer Series: Vectors II: Vector Operations
In the last installment of this math primer, we looked at the difference between points and vectors. Today, we’ll dive a little bit deeper into vectors, and the specific operations we can perform on them. More importantly, we’ll take a look at the geometric significance of the many operations, and how they can help us in building a game.
We’ll focus primarily on unary and binary operations of vectors. There are a few interesting ternary operations as well, but I’ll leave those for interested readers to follow up on independently. They’re not nearly as prevalent in game code. As always, see the references section of the initial Math Primer post for further reading.
Addition and Subtraction
The most basic binary operations we can do on vectors are addition and subtraction. Adding two vectors is as simple as it sounds; we create a new vector whose components are the sums of the corresponding components from the initial two vectors:
Subtraction is equally simple, we just subtract the components of the second vector from the first. However, there’s an assumption we’re making in order to subtract. That is, we’re assuming that there is such a thing as inverting a vector to a vector with equal but negated components, since subtraction is really just addition with the inverse (negation) of the second vector. Well, it turns out that our assumption is actually correct. It is possible to invert a vector, which multiplies each component by –1. This inverse vector has the same magnitude as the original vector, but opposite direction.
Now, why would we ever want to add or subtract vectors? Well, the answer lies in the geometric significance of these operations. Adding two vectors gives a single vector that has the same direction and magnitude as following each of the addend vectors back to back. Let’s look at a diagram:
In this picture, the two black vectors represent the vectors being added together, and the dashed blue vector is where you end up after following the two vectors in order. This is exactly equal to the sum vector obtained by adding the two vectors component-wise as we did above. Again, subtraction is similar, just inverting one of the vectors (reversing it’s direction, but otherwise leaving it oriented the same way and the same length). See Figure 2.
Scaling
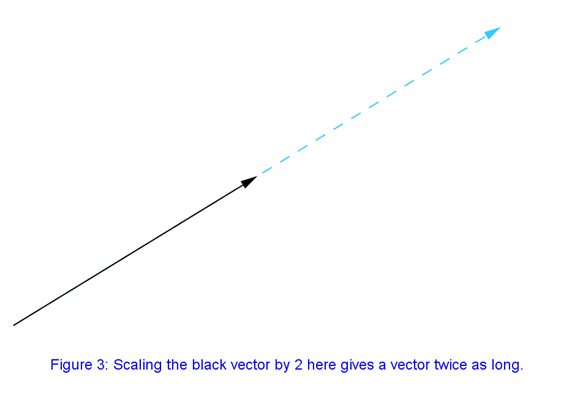
Before we dive into multiplications between two vectors, it’s worth taking a quick look at a simple scaling operation. We can multiply (or scale) a vector by any scalar value by simply multiplying each component of the vector by that value:
The geometric significance of this is that it scales the length of the vector by s, leaving the direction as it is.
Dot Product
The first type of multiplication between vectors we’ll look at is called the scalar product, also called the dot product or inner product. As the name scalar product implies, the result of this type of multiplication is actually a scalar value, and not a vector. To compute the scalar product of two vectors, we sum the component-wise products of each vector:
Notice the dot-like symbol for the scalar product. This is why it’s most commonly called the dot product. The dot product is perhaps the most commonly encountered vector operation in game and graphics code. There are several reasons for this, not least of which is the geometric significance of the dot product. The dot product of two vectors gives the scaled length of the projection of one vector in the direction of another. What does that mean exactly? Said another way, it tells you how much of a vector is in the same direction as another vector:
On the left half of this figure, we see two vectors. We wish to determine how much of the first vector lies in the direction of the second vector. This is exactly what the dot product gives us. On the right half of the figure we see the two vectors again, this time with their tails placed together. We can visibly see that the portion of the vector in the direction of the other is equal to the blue arrow. The dashed red line shows that this forms a right triangle. The dot product of the two original vectors is equal to the length of the blue vector (the projection) scaled to the length of the second vector (the one the blue vector is overlapping). If this vector is of unit length, then the dot product is exactly the length of the blue vector, or projection of the first vector onto the second.
Another major reason the dot product is popular in game and graphics code is that the dot product of two vectors is equal to the cosine of the angle between them, scaled by the lengths of both vectors:
On a final note, before moving on to other forms of vector multiplication, it’s worth noting that scalar products are commutative:
Cross Product
The vector product, also called outer product or cross product, is the next and final form of multiplication we’ll look at in depth. There are other types of vector multiplication, such as the Hadamard product and tensor product, but they either don’t appear often in game programming, or are the topic of later discussions (we’ll revisit tensor product when talking about matrices). As the name vector product implies, this product results in a vector and not a scalar:
The equation, as well as how we arrive there, will become more clear when we look at matrix operations in the later chapters of the primer. Now, why is the cross product important? Before we answer that, let’s take a very quick detour and discuss coordinate systems and coordinate handedness.
A coordinate system is a representation that we impose onto a space so that we can describe it. What coordinate system we use to describe something has absolutely no bearing on the object itself, only on the description we use. Let’s look at a comparison of two arbitrary coordinate systems and the same object represented in both:
Here we have the same cube in the same space, with two arbitrarily selected coordinate systems drawn. We can see that the cube is the same regardless of how we’ve selected our coordinate space, however describing that cube will differ. Using the first coordinate system, I might say “the cube is out a few units along the x-axis, and a few units forward along the z-axis”. Using the second coordinate system, I might say “the cube is out a few units along the y-axis, and a few units back along the x-axis”. Clearly, these descriptions are different, though we’re talking about the same cube.
What we’ve shown here is that it really doesn’t matter what coordinate system you use. There is no single correct, or universal, coordinate system. Different games and graphics packages use different systems. What’s important is that everything which uses the coordinate system needs to agree on a single system and remain consistent. Otherwise, a seemingly correct description from the perspective of one part of the code might be complete nonsense to another part. For this blog, I’ll try not to assume any particular system and generically refer to the 3 axes as ‘right’, ‘up’, and ‘forward’ where I can. You can label these anything you like.
Now, we mentioned handedness of a coordinate system. What we mean by that is the orientation of the 3 axes that make up our 3D coordinate system. There are two possible orientations, shown in the two images above. As we can see, the axis pointing up and the axis pointing to the right are the same between the two coordinate systems, but the third axis points towards us in one case and away from us in the other. While you can make the first two axes point in any direction, what you’ll find when laying out coordinate systems is that they will always end up in one of two formations. These are called left-handed and right-handed systems. The easiest way to tell which is which is by taking your right hand and pointing your fingers all along the ‘right’ axis, then bend your fingers in the direction of the ‘up’ axis. If you’re thumb is pointing in the direction of the forward axis then you’ve got a right-handed system. Otherwise, it’s a left-handed one. In the figure above, the first one is right-handed, and the second one is left-handed.
That’s enough of a detour, let’s get back to the cross product! The most important geometric significance of the cross product (for games) is that the resulting vector will be pointing in a direction that is orthogonal to the two vectors we multiplied. However, you’ll notice that there are two possible results here. They are equal but pointing in opposite directions. See the two red vectors in the figure below:
Which of the two cross products you get depends entirely on the handedness of the coordinate system you’re using to represent your vectors. This works for any coordinate system, but as an example let’s take the first coordinate system in Figure 4. We could express our vectors in terms of (x, y, z). If we were to use the same coordinate system but make it left-handed (invert z in this case), then our vectors would be expressed in terms of (x, y, –z). From the cross product equation above, you can see that this would negate some of the terms, which when multiplied out can be shown to return the inverse of the cross product computed with (x, y, z). To look at it another way, you can use your hand again (use the hand that matches the handedness of the coordinate system) and point your fingers in the direction of the first vector being multiplied. Then curve your fingers in the direction of the second vector. The cross product will point in the direction of your thumb.
The other geometric property, though used less often, is that the length of the cross product is equal to the sine of the angle between the vectors scaled by the lengths of the two vectors. This is exactly the same as with dot product, except sine instead of cosine:
Finally, we should note that cross products are not commutative.
Magnitude and Normalization
The final two operations we’ll take a look at are unary operations on a single vector. The first is determining the magnitude of a vector, which is computed using the following equation:
The final one is called normalizing a vector, which is to scale the vector to a length of 1, while maintaining it’s direction. This is done by simply dividing the vector by it’s magnitude.
The ^ symbol over a vector is used to denote that the vector is normalized, or of unit length.
That’s all for this chapter of the math primer. Hopefully that helped clear up and explain some of the elementary operations we’ll be needing throughout our work on physics and game code in coming posts. Please feel free to let me know if I’ve made any mistakes or if I could explain something further or better.
Comments
Anonymous
June 06, 2011
The comment has been removedAnonymous
June 06, 2011
Thanks for pointing that out, I'll take a look and see if I can figure out how to fix it.Anonymous
June 27, 2011
I sure hope you get the time to continue these. I found you by accident and it has been a blessing. I enjoy your articles and plan to follow you closely in the future I have already learned so much you explain every thing perfectly thanks a million. `BakerAnonymous
July 21, 2011
You might want to explain unit length vectors a bit before using them in the discussion. Also, basis vectors, somewhere.Anonymous
September 05, 2011
Thanks, very good explanations about the "significance" of dot and cross productsAnonymous
November 04, 2013
Thanks, excellent explained.Anonymous
September 08, 2014
Very beautiful explanation :)Anonymous
September 28, 2014
Thanks for these. Very clear explanations.
![clip_image002[38] clip_image002[38]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/7587.clip_image00238_thumb_2426FDA3.gif)
![clip_image004[20] clip_image004[20]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/0638.clip_image00420_thumb_4EFF61B5.gif)
![clip_image006[17] clip_image006[17]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/2388.clip_image00617_thumb_6EAE3B7D.gif)
![clip_image002[40] clip_image002[40]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/3872.clip_image00240_thumb_75614500.gif)
![clip_image004[22] clip_image004[22]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/4035.clip_image00422_thumb_42FD7181.gif)


![clip_image002[54] clip_image002[54]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/4760.clip_image00254_thumb_45B11B72.gif)
![clip_image002[42] clip_image002[42]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/8664.clip_image00242_thumb_4944480F.gif)
![clip_image004[24] clip_image004[24]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/8662.clip_image00424_thumb_6CFD6FA9.gif)
![clip_image006[20] clip_image006[20]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/4035.clip_image00620_thumb_0CAC4972.gif)


![clip_image002[44] clip_image002[44]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/7563.clip_image00244_thumb_2C5B233A.gif)
![clip_image002[46] clip_image002[46]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/4353.clip_image00246_thumb_24BDA8CB.gif)
![clip_image002[48] clip_image002[48]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/1122.clip_image00248_thumb_1274E209.gif)
![clip_image004[26] clip_image004[26]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/6835.clip_image00426_thumb_002C1B47.gif)
![clip_image006[22] clip_image006[22]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/1526.clip_image00622_thumb_71EDA256.gif)

![clip_image002[58] clip_image002[58]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/1145.clip_image00258_thumb_211A301E.gif)
![clip_image002[50] clip_image002[50]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/7080.clip_image00250_thumb_6FD0A38D.gif)
![clip_image002[56] clip_image002[56]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/45/26/metablogapi/4760.clip_image00256_thumb_48965A58.gif)